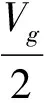考虑热膨胀差影响的双锥密封性能研究与应用
2019-05-31
(1.上海森松压力容器有限公司,上海 201323;2.上海市特种设备监督检验技术研究院,上海 200062)
0 引言
双锥密封是一种保留设备主螺栓的半自紧式径向密封结构,其最大的特点是双锥环的内圆柱面与平盖的圆柱支撑面之间留有适当的初始径向间隙g(文中所用符号,除新增加和特别注明外,与GB/T 150.3—2011的定义一致),典型的双锥密封结构见图1。在预紧时,通过拧紧螺栓,使夹在密封锥面之间的软垫片被压紧,并达到设计规范要求的预紧密封比压(qa,min=y);同时,通过斜楔原理,使双锥环产生径向压缩的弹性变形,双锥环的内圆柱面会逐步向平盖的圆柱支撑面靠近,直到初始径向间隙g被彻底消除(此时,直径间隙ΔD=0)。当内压升高时,平盖被向上抬起,螺栓被继续拉伸变长,软垫片上的密封比压将从预紧时的qa减小为操作时的q;同时,内压施加在双锥环的内圆柱面上所产生的径向扩张力Vp也从零开始逐步增加。为了弥补因平盖抬起产生的密封锥面之间的间隙,预先被压缩的双锥环立即回弹,并产生弹性径向扩张力VR,从而在密封锥面上仍然维持一定的操作密封比压(q≥mp)。由于双锥环的回弹,原来双锥环内圆柱面与平盖的圆柱支撑面之间紧贴的状态也会开始分离,并出现直径间隙(ΔD>0)。

(a)剖视图

(b)软垫片
这种密封型式具有结构简单、易于加工的优点,并且装拆十分方便,对压力与温度波动具有自适应性,从而得到十分广泛的应用。根据GB/T 150.3—2011《压力容器 第3部分:设计》的规定,这种密封结构适应于设计压力6.4~35 MPa,温度0~400 ℃,内径400~3 200 mm的范围。但是,目前的标准和文献没有对高温工况下双锥密封系统各元件之间可能产生的热膨胀差或实际操作过程中温度波动的影响进行系统地考虑[1-13]。特别是,对于双锥环的材料与平盖、筒体端部的材料不一致时,造成有些设备在开停车及操作过程中出现泄漏现象。由于没有可靠的理论解释和计算方法,只能通过试验和有限元建模来进行验证[4]。文献[3]仅从泄漏试验来验证升温过程对铝垫片的密封性能影响不显著;文献[4]仅从数值模拟计算结果验证双锥密封间隙大小对温度波动适应性的影响;文献[5]仅考虑了恒定高温下由于材料力学性能降低对密封性能的影响;文献[6]仅对操作过程中温度波动对密封性能的影响进行了定性分析。因此,目前仍缺乏系统的理论分析和研究。
本文在文献[1]的基础上,进一步研究热膨胀差对高压双锥密封性能的影响;运用变形协调原理和内力平衡方程,将预紧与操作两个工况之间的热膨胀差引入双锥密封机理,提出“热当量间隙ΔU”的概念,并关注其对操作密封比压q、拐点压力pc、最小操作密封比压qc的影响。同时,考虑热当量间隙后,推导在操作工况下的螺栓载荷Wo计算通用公式,并以此分析和解决实际高温高压容器双锥密封的泄漏问题。
1 考虑热膨胀差影响的双锥密封系统的变形协调[14-15]
假设平盖和筒体端部均为刚体(忽略其弹性变形,仅考虑热膨胀引起的变形),双锥环只考虑径向弹性变形,忽略其轴向压缩和弯曲变形。
1.1 预紧工况双锥密封系统的轴向变形总量
(1)
式中Wa——预紧工况时的螺栓载荷,N·mm;
LB——螺栓热当量长度,mm,LB≈h1+h;
h1——平盖在双锥环密封槽处的最小厚度,mm;
h——双锥环的有效高度,mm,h=(A+C)/2;
n——螺栓数量;
fB——单个螺栓的根部截面积,mm2;
EB,a——螺栓在常温下的弹性模量,MPa。
1.2 操作工况双锥密封系统的轴向变形总量
(2)
其中:
UZ=LBαB(TB-Ta)-δFαF(TF-Ta)
-hαR(TR-Ta)
UD=DG[αF(TF-Ta)-αR(TR-Ta)]
式中Wo——操作工况时的螺栓载荷,N·mm;
EB——螺栓在操作温度下的弹性模量,MPa;
UZ,UD——系统的轴向热膨胀松弛量和直径方向热膨胀松弛量,mm;
ΔD1——操作工况下双锥环的残余直径压缩量,mm;
αB,αF,αR——螺栓、法兰盖、双锥环在操作温度下的平均热膨胀系数,mm/(mm·℃);
TB,TF,TR——螺栓、法兰盖、双锥环在操作工况下的平均金属温度,℃;
Ta——预紧工况下的环境温度,℃,一般取20 ℃;
δF——法兰盖的热当量厚度,mm,
δF≈h1+(A-C)/2;
DG——垫片压紧力作用中心圆直径,mm。
1.3 变形协调方程和热当量间隙
为了满足操作工况下密封系统各元件之间仍保持接触状态,应有Ua=U成立[10]。
令ΔU=-(UZtanα+UD),ΔD0=2g+ΔU,得:
(3)
式中D0——在操作工况下,温度为操作温度、压力p=0时的热态初始直径压缩量,mm。
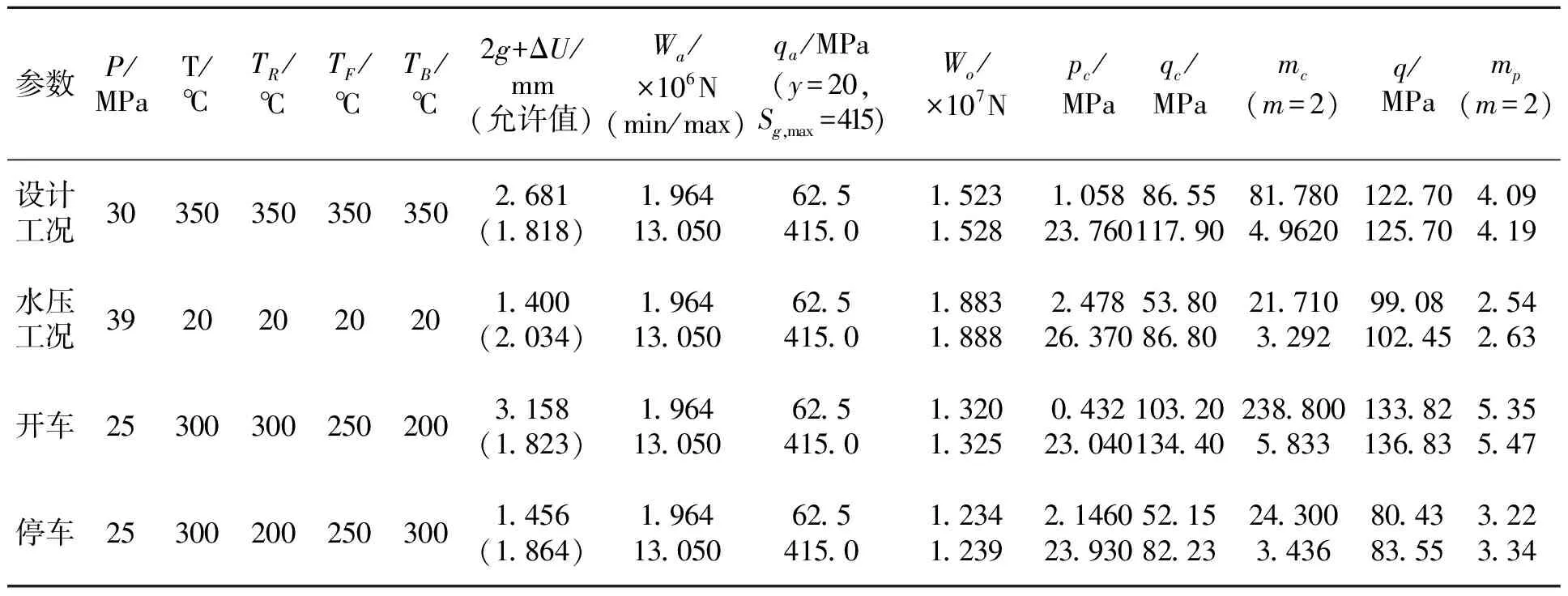
令ΔD=ΔD0-ΔD1,即:在操作工况下,压力p=0时双锥环的热态初始直径压缩量ΔD0减去压力上升至任意压力(0 ΔU=[δFαF(TF-Ta)+hαR(TR-Ta)-LBαB ×(TB-Ta)]tanα+DG[αR(TR-Ta) -αF(TF-Ta)] ΔU就是热当量间隙,即:在操作工况下,温度上升至操作温度、介质压力p=0时,在预紧工况的初始直径压缩量2g的基础上,因热膨胀差引起的直径压缩量的增加值。当ΔU>0,表示双锥环被进一步压缩;当ΔU<0,表示双锥环被松弛。 于是,变形协调方程式(3)可简化为: (4) 上面两公式左边就是螺栓在操作时相对于预紧时的伸长增量ΔLB,可进一步简化为: (5) 式(5)与文献[1]的几何方程ΔD=ΔLtanα类似,但是,由式(4)可知,这里考虑了热当量间隙ΔU和高温对螺栓材料弹性模量的影响系数EB/EB,a。 2.1.1 预紧工况下双锥环的受力分析[6-7] 预紧工况下双锥环受力分析如图2所示。当双锥密封结构预紧时,应该保证的条件为:(1)密封面上的软垫片要达到初始的密封条件;(2)双锥环产生的径向压缩量足以消除双锥环与平盖支撑面之间的初始径向间隙g。 图2 双锥环几何尺寸与预紧工况下受力分析 (1)密封面上的软垫片要达到初始的密封条件。 设软垫片的预紧密封比压qa,min=y,为实现预紧密封所需的螺栓预紧力Wa,1等于图2(b)中密封面上的摩擦力Fm和接触压力N0在垂直方向上的分力之和: (6) 其中: (2)双锥环产生的径向压缩量足以消除双锥环与平盖支撑面之间的初始径向间隙g。 在预紧时,双锥环会由于受压而产生径向收缩,这部分储存的弹性能将在回弹时得到释放。因此,为尽可能地增加回弹力,一般需要将双锥环压缩至初始径向间隙g完全消除为止。此时,水平方向回弹力VR,a为 : (7) 式中fR——双锥环的截面积,mm2,fR=AB- 式(7)表示了当双锥环直径收缩2g时所引起的回弹力。这个周向均布力分别从双锥环上下两个锥面作用于平盖和筒体端部的两个密封锥面上,每个锥面所承担的回弹力为VR,a/2,此力在轴向引起的分力FR,a就等于为消除初始径向间隙g所需的螺栓预紧力Wa,2,即:FR,a=Wa,2。 (8) (3)在预紧时,条件(1),(2) 必须同时满足。 实际预紧载荷Wa应满足: Wa≥max(Wa,1,Wa,2) (9) 由式(6),(8)可知:当直径较小、y也较小时,Wa,1 在预紧时,由于必须是Wa>Wa,2,那么,在双锥环内侧圆柱面和平盖支撑圆柱面之间一定会产生一个额外的支撑反力Vg,a,根据水平内力平衡方程,其大小为: Vg,a=Va-VR,a (10) 式中Va——摩擦力Fm和接触压力N0的合力在水平方向上的分力,N。 由图2可知: (11) 将式(6)中的y替换成qa,Wa,1替换成Wa,可得实际初始密封比压qa: (12) 2.1.2 螺栓预紧载荷的最小值 为了能实现初始密封,且消除初始间隙g,螺栓预紧载荷的最小值Wa,min应取Wa,1,Wa,2二者的最大值,即: Wa,min=max(Wa,1,Wa,2) (13) 2.1.3 螺栓预紧载荷的最大值 螺栓预紧载荷的最大值Wa,max,一般是由软垫片或双锥环被压溃的最大应力qa,max=Sg,max决定的。Sg,max的取值参见文献[16-17]。 将式(6)中的y替换成Sg,max,Wa,1替换成Wa,max,得: (14) 操作工况下双锥环的受力分析如图3所示。操作螺栓载荷Wo为以下四部分之和: (1)作用在平盖上的内压平衡的螺栓轴向力F; (2)作用在双锥环内侧圆柱面上的内压平衡的螺栓轴向力Fp; (3)双锥环水平方向回弹力平衡的螺栓轴向力FR; (4)双锥环水平方向受平盖圆柱支撑面挤压力平衡的螺栓轴向力Fg。 因此,根据垂直内力平衡方程,螺栓载荷可表示为: Wo=F+Fp+FR+Fg (15) 图3 操作工况下双锥环受力分析 2.2.1 作用在平盖上的内压平衡的螺栓轴向力F (16) 2.2.2 作用在双锥环内侧圆柱面上的内压平衡的螺栓轴向力Fp 当工作压力作用在双锥环内圆柱面上时会引起双锥环的径向扩张,这个水平力Vp为: Vp=πDGhp (17) 由于双锥环向外扩张时,平盖和筒体端部相对双锥环锥面向顶端移动,相对运动趋势与预紧时的运动趋势相反,因而摩擦力Fm的方向也与预紧时相反。由力的平衡关系,可得双锥环锥面处作用力的垂直分量Fp: (18) 2.2.3 双锥环水平方向回弹力平衡的螺栓轴向力FR 操作状态下,双锥环内圆柱面与平盖之间的直径间隙ΔD会在0~ΔD0(即:2g+ΔU)的范围内变化;甚至,当压力p足够大时,使双锥环产生反向(拉伸)变形,但是不能超过(2g+ΔU),否则,双锥环会产生塑性拉伸变形,造成棘轮垮塌失效。实际上,由于螺栓的刚度远大于双锥环的刚度,加上双锥环与平盖和筒体端部为楔形密封,产生的直径间隙ΔD会很小,一般还不到初始间隙的一半。 水平方向回弹力VR: (19) 此时作用在一个锥面上的水平方向回弹力为VR/2,与双锥环水平方向回弹力平衡的螺栓轴向力FR等于密封面上的摩擦力Fm和接触压力N在垂直方向上的分量之和: (20) 假定双锥环在操作状态下,其内圆柱面仍与平盖支撑圆柱面接触,即两者间隙为零(ΔD=0,ΔD1=ΔD0),这种情况下双锥环的回弹力最大,即可得到VR,max和FR,max。 2.2.4 双锥环水平方向受平盖圆柱支撑面挤压力平衡的螺栓轴向力Fg 在操作工况下,如果双锥环的内圆柱面仍与平盖圆柱支撑面贴合(ΔD=0),双锥环所承受的水平挤压力为Vg(Vg>0),那么其引起的垂直螺栓载荷Fg为: (21) 其中,Vg的计算公式参见第3.1节的式(28)。 当p=0时,Vg最大,即可得到Vg,max。 2.2.5 操作工况下的螺栓载荷Wo 当压力上升至任意压力(0≤p≤pmax,且p>pc)时,双锥环的内圆柱面与平盖圆柱支撑面之间存在间隙(ΔD>0),那么双锥环所承受的水平挤压力为零(Vg=0)。于是,将式(16),(18),(20)代入式(15),即可得到操作工况下主螺栓载荷Wo: (22) 当压力上升至任意压力(0≤p≤pmax,且p≤pc)时,双锥环的内圆柱面与平盖圆柱支撑面仍贴合(ΔD=0),那么双锥环所承受的水平挤压力Vg>0。于是,将式(16),(18),(20),(21)代入式(15),即可得到操作工况下螺栓载荷Wo: (23) 设操作工况时的密封比压为q,那么双锥密封面上的法向接触压力[1]为: N=πDGbq (24) 根据图3,可得其水平总分力为: (25) 水平内力平衡方程: V=VR+Vp+Vg (26) 式中Vg——双锥环内圆柱面与平盖支撑面之间的相互挤压力,N。 在预紧工况时,已知Vg,a=Va-VR,a;在操作工况时,Vg=V-VR-Vp,且存在以下4种情况。 (1)当压力还没开始上升(p=0,ΔD=0,Vp=0),仅温度已达到操作温度,此时V=VR,max+Vg,max。 (2)开始升压,但是压力还没有上升到使双锥环内圆柱面离开平盖支撑面(0 (3)当压力上升到使双锥环内圆柱面刚刚离开平盖支撑面(p=pc,ΔD=0,Vg=0),此时V=VR,max+Vp。这个使贴合面即将分离的压力pc称为“拐点压力”。 (4)当压力上升到使双锥环内圆柱面离开平盖支撑面(p>pc,ΔD>0,Vg=0),此时V=VR+Vp。 由水平内力平衡方程V=VR,max+Vp+Vg,可得密封比压: (27) 由式(4)和式(23),联立求出Vg: ×tan(α-ρ)]} (28) 将上式代入式(27),得: (29) 在任意压力p时的密封系数mp=q/p。 由水平内力平衡方程V=VR+Vp,可得密封比压: (30) 由式(4)和式(22),联立求出ΔD: (31) 将上式代入式(30),得到: q=Mp+N (32) 其中: 注意:文献[1]中相应M,N公式的第二项的分母部分疑似漏掉了D1,否则,其量纲就不对了,导致其公式无法使用。 在任意压力p时的密封系数mp=q/p。 将式(31)取值为0(即令ΔD=0),可知拐点压力pc为: (33) 将上式和ΔD=0,ΔD0=2g+ΔU代入式(30),可得最小操作密封比压qc为: (34) 那么,与最小操作密封比压qc对应的拐点密封系数mc=qc/pc。 注意:对于全压力区间(0≤p≤∞),qc是对应的最小操作密封比压(见图4(a)),但是,mc不是对应的最小密封系数,密封系数随压力的增加而单调地减小(见图4(b))。因此,mc只是拐点压力pc对应的拐点密封系数,而不是对应的最小密封系数。也就是说,当0≤p≤pc时,mc就是这一压力区间的最小值;当pc≤p≤∞时,mc就是这一压力区间的最大值(见图4(b)中任意一根mp-p曲线)。 表1列出本文方法与现行标准GB/T 150.3中方法的对比分析。从表1得出如下结论。 (1)GB/T 150.3—2011中的预紧载荷仅考虑了Wa,1,默认Wa,1>Wa,2始终成立,其实是考虑不周全的。 表1 本文方法与现行标准GB/T 150.3中方法的对比分析 因本文的实际操作螺栓载荷Wo的计算与实际预紧载荷Wa决定的拐点压力pc有关,应根据设计压力pmax所处区间来确定采用哪个计算公式。 (3)由于GB/T 150.3中方法没有考虑操作工况下的密封参数,就无法优化预紧螺栓载荷Wa,也无法优化密封结构(软垫片的m,y,Sg,max,双锥环材料的ER,αR和双锥环结构尺寸b,h等)。 由上述分析可知,预紧载荷Wa增加,拐点压力pc也随之增加,而拐点密封系数mc反而下降。所以,即使mc>m,满足操作密封要求,也不能保证在pc≤p≤pmax这段工作压力区间时有mp>m。但是,如果p 当预紧载荷Wa增加到使拐点压力接近、甚至超过设计压力(pmax≤pc)时,临界密封系数mc反而更小,此时,已成为“自紧密封+强制密封”。因为,在0≤p≤pmax的全工作压力区间内ΔD=0(双锥环内圆柱面一直没有与平盖圆柱支撑面分离)。这时,如果mc>m,可满足全工作压力区间内的mp>m。但是,预紧载荷也不能太大,否则会导致双锥环密封面因实际预紧比压过大(qa>Sg,max)而被压溃失效(即:当有软垫片时,垫片会被挤破或压瘪;当没有软垫片时,双锥环因挤压塑性变形过大,最多使用一次,开盖后就需要更换,甚至法兰密封面都会被挤出压痕)。因此,需要规定最大预紧载荷Wa,max;而且,当没有软垫片时,需规定双锥环材料的硬度要低于法兰密封面材料的硬度HB20~HB30,以保护法兰密封面。 典型的Wa对q-p曲线和mp-p曲线的影响见图4。 (a)q-p曲线 (b)mp-p曲线 注:系列1和2对应Wa-1的曲线,系列3和4对应Wa-2的曲线,系列5和6对应Wa-3的曲线,且Wa-1 图4Wa对q-p曲线和mp-p曲线的影响 宁波某工厂于9年前从台湾省购买的多台高压换热器,管箱采用从欧盟进口的VECTOR专利双锥密封,没有采用软垫片来隔离双锥环和法兰密封面(y=179.3 MPa,m=6.5)。水压没有问题,但是经过几次开停车后,发生了泄漏,每次修理需研磨管箱筒体端部和平盖的密封锥面,并更换双锥环。其密封环尺寸:A=44.3 mm,B=17.8 mm,C=30 mm,α=15°,D1=867.35 mm,比国内标准规定的要小,据说是经过有限元分析优化的结果,虽然对平盖的削弱减少了,但是,密封不可靠。 委托某公司分析泄漏原因,并进行改造。经查看原计算书,发现原设计的初始间隙g(g=2.55 mm)高达0.294%D1,预紧载荷高达70%螺栓屈服极限。由于采用特殊的法兰结构,其预紧载荷被限定在由双锥环的回弹力控制的预紧螺栓载荷Wa,2以内,也不会产生平盖圆柱支撑面对双锥环内圆柱面的支撑反力(Vg,a=Vg=0),操作时的直径间隙也可以认为一直维持为零(ΔD=0),这样,双锥环不会受到因预紧载荷过大而导致的过度挤压塑性变形。但是,由于初始预紧间隙g过大,致使双锥环被严重压缩屈服变形,加上密封面为较软的316L堆焊材料,而双锥环为较硬的N06625材料,且在双锥环和法兰密封面之间没有软垫片,造成法兰密封面在双锥环的挤压下就已经被局部压溃塑性变形,从而无法确保理论的预紧比压qa和操作密封系数mc,mp与实际相符合,即:理论计算值失去了实际意义。于是,每打开一次,就要更换双锥环,并研磨法兰密封面,但是,开车后没多久就滴漏不断。改造前设计参数和计算结果见表2(2g或2g+ΔU的允许值是参考文献[8]中的计算方法)。 表2 改造前双锥密封的设计参数和计算结果 从图2计算结果可以看出,各工况的2g+ΔU均大于允许值,特别是开车时超出允许值约1倍;首先,理论的预紧比压qa就达不到设计规范要求的y值(由于没有软垫片,y值很大);虽然水压的理论密封系数(mc,mp)均达不到设计规范要求的m值,但是水压密封合格,只能说明它们的加工精度高,加上冷水也是较为容易密封的缘故。 采用堆焊来填平原法兰密封面的凹槽,重新按GB/T 150.3—2011在内径侧加工新的法兰密封面,双锥环采用316L材料,平盖按标准结构加厚并采用20MnMo堆焊316L材料。其密封环尺寸如下:A=71 mm,B=29 mm,C=36 mm,α=30°,D1=700 mm,初始间隙g按设计规范取中间值 0.1%D1(g=0.7 mm),控制预紧载荷在Wa,min~Wa,max之间,并采用厚度为0.8 mm的柔性石墨软垫片(y=2 MPa,m=20,Sg,max=415MPa[12])。改造后设计参数和计算结果见表3(2g或2g+ΔU的允许值是参考文献[8]中的计算方法)。 表3 改造后双锥密封的设计参数和计算结果 从图3计算结果可以看出,仅设计和开车工况的2g+ΔU超出允许值的47%~73%;理论的预紧比压qa和理论密封系数(mc,mp)均满足设计规范要求的y值和m值,说明密封是可靠的。尽管设计和开车工况的2g+ΔU超出允许值,但是,其对应的理论的预紧比压qa和理论密封系数(mc,mp)均高出设计规范要求的y值和m值很多,可以弥补因过度压缩变形引起的实际密封性能的下降。成功改造一台后,又陆续由该公司改造了多台类似的高压管箱密封结构。 上述计算结果,如按现有设计标准GB/T 150.3—2011是无法得到的,也发现不了这些内在问题。因此,希望标准修订时能考虑上述因素,使双锥密封设计更加可靠。 (1)本文运用变形协调原理和内力平衡方程,系统地将热当量间隙ΔU引入双锥密封机理,并推导了包含热当量间隙ΔU影响的操作密封比压q、密封系数mp以及拐点压力pc、最小密封比压qc、拐点密封系数mc的计算公式。同时,推导了包含热当量间隙ΔU影响的、在操作工况下的螺栓载荷计算通用公式。 (2)GB 150.3—2011中的螺栓预紧载荷Wa,没有考虑由软垫片被压溃的最大垫片应力Sg,max决定的最大螺栓预紧载荷Wa,max的影响,这就造成实际预紧时的盲目性,而本文给出了系统的计算方法。 (4)通过改造实例说明,我国的双锥密封设计标准结构是可靠的,能适应高温高压的开停车工况,不比国外的专利密封结构差。 (5)建议GB/T 150.3—2011在修订时,考虑热当量间隙ΔU对各种操作工况下的热态初始直径压缩量ΔD0、最小密封比压qc、操作工况的螺栓载荷Wo等计算公式的影响,进一步完善设计标准应考虑的各种密封参数(q,mp),使双锥密封设计更加可靠。
2 考虑热当量间隙的双锥密封原理及公式推导
2.1 预紧工况
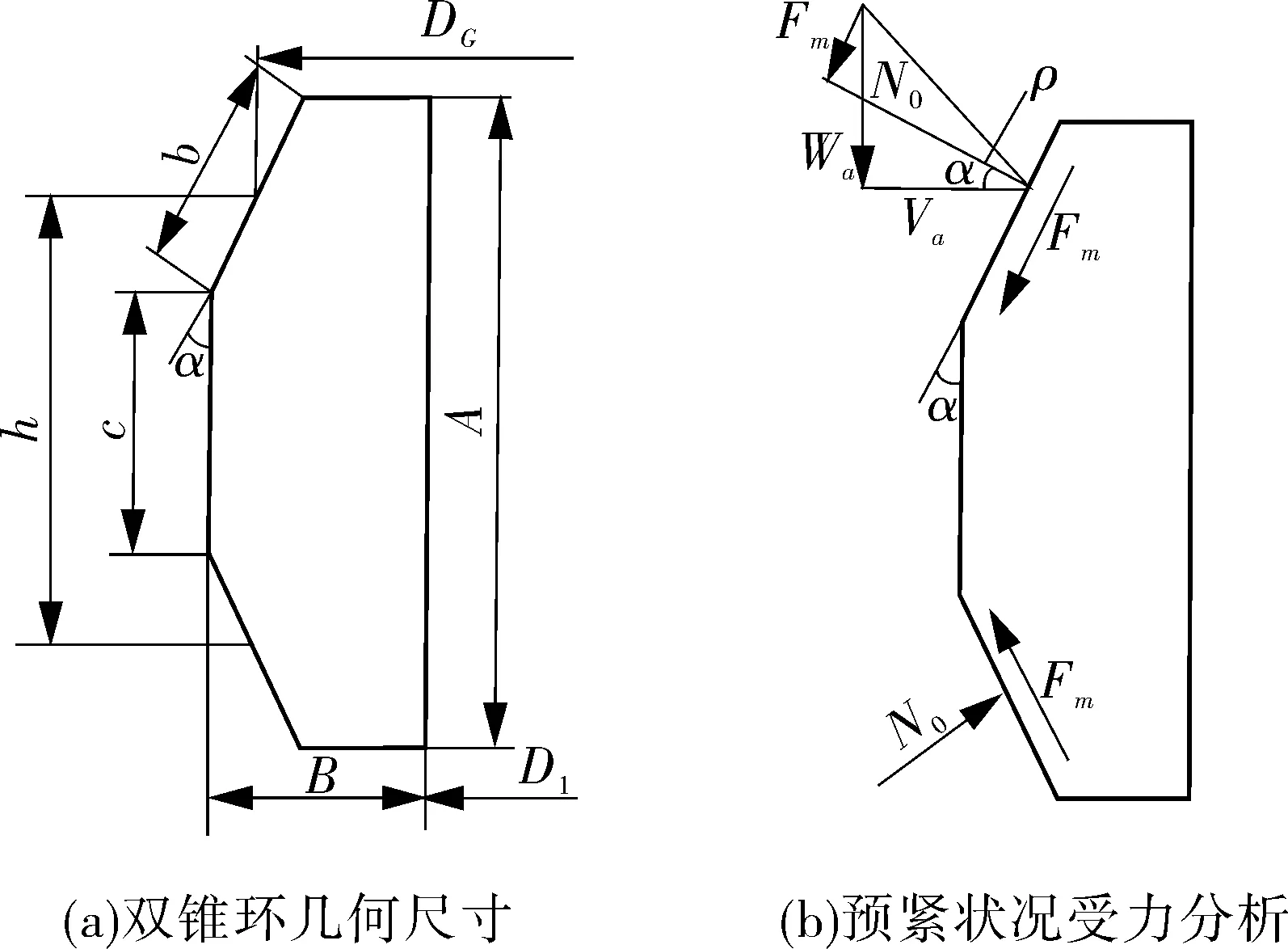


2.2 操作工况下双锥环的受力分析[6-7]


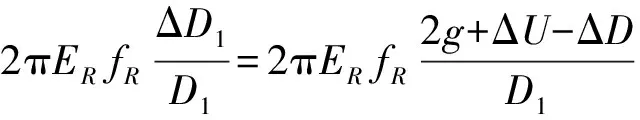





3 考虑ΔU后的操作密封比压q和密封系数mp
3.1 考虑0≤p


3.2 考虑pc≤p<∞,ΔD≥0,Vg=0,即(3)和(4)两种情况


4 拐点压力pc、最小密封比压qc、拐点密封系数mc[1,8]
5 本文方法与现行标准GB/T 150.3方法的对比分析


6 预紧载荷Wa对双锥密封性能的影响分析


7 应用实例[18-19]
7.1 实例基本情况

7.2 改造后的双锥密封
8 结语