基于改进卷积反投影模型的CT成像伪影消除方法*

韩寅奔， 董泉润

(西北工业大学 a. 教务处， b. 动力与能源学院， 西安 710072)

随着现代工业的发展，计算机断层成像(computed tomography，CT)技术被越来越多地运用到无损检测和逆向工程等行业中[1].CT重建是一种无损检测技术，其利用精确准直的X射线在不破坏被测物体的前提下，根据被测物体不同组织结构吸收射线能力的差异性对被测物体进行断层成像，能省时、无损地探测物体内部情况，获取内部结构信息[2-4].

目前，常用的CT重建算法主要有迭代法和解析法两种[5].迭代法能处理不同方式的采样数据，且能获得稀疏采样数据的重建图像，但该种方法需要较大的计算量，重建速度较慢[6-7]；解析法中最具代表性的是卷积反投影法，其通过处理完全等间距的投影数据来获得更好的成像质量和更快的成像速度，但这种方法得到的重建图像容易产生伪影[8-9].

相比于迭代法，卷积反投影法的应用范围更广.许多专家和学者提出了诸多方法来提高卷积反投影法的重建速度与成像质量，消除伪影.在提升重建速度方面，文献[10]基于极坐标的特性，提出了一种PCBP重建算法，但其在坐标转换过程中需要较大的计算量；文献[11]基于正余弦函数的特性，同时重建16幅采样图像，明显提升重建速度；文献[12]则基于三角函数的对称性，使用对称优化算法同时重建64幅图像.而在提升成像质量方面，文献[13]通过分析不同伪影的种类和成因，分别消除各种医学图像的伪影；文献[14]则基于周期性原理，使用正切函数来优化重建图像，但这种方法得到的重建图像仍存在部分伪影.

针对上述问题，本文提出了一种基于卷积反投影算法的CT成像伪影消除方法.首先分析并标定给定模板的测量参数；然后使用Radon和傅里叶变换得到反投影方程，并计算每一点吸收率与投影值的积分关系，从而得到较清晰的重建图像.

1 参数标定

使用CT系统进行无损检测时，保持射线源和探测器不动.CT系统探测模板与着色图及其坐标系示意图如图1所示.为采集不同旋转角度的投影信息，探测物包含椭圆和圆形两个模板.然而，理论上旋转中心与射线源焦点的连线是垂直于探测器的，但是在安装CT系统时，难以实现这一要求，通常存在误差，并导致重建图像存在伪影.因此，需要对安装好的CT系统进行参数标定，即借助模板标定CT系统的参数，并使用这些参数对未知结构的样品进行成像.

本文首先绘制模板投影信号着色图，得到模板旋转轨迹.图1b中用黄色表示投影信号强度为零，并用深浅不同的蓝色表示不同强度的投影信号，强度越高，颜色越深；然后以着色图左下角为原点，横轴表示旋转角度，纵轴表示其探测器端点的距离，建立直角坐标系；最后结合着色图的几何特征，建立其与实际照射情况的对应关系，并在此基础上标定CT系统的旋转中心、探测器单元间距离及探测方向等参数.

图1 探测模板与着色图及其坐标系Fig.1 Detection template，coloring diagram and coordinate system

1.1 探测器单元间距离

当X射线平行于椭圆长轴入射时，光在介质中走过的路径最长，衰减幅度最大，接收到的信号最强.此时，椭圆模板在接收器上的投影长度最短且恰为短轴长，即图1b中A、B两点的纵坐标之差.测得AB之间共有L个单元格，即对应L-1个探测单元间距，故可得探测器单元间距离d=m/(L-1)，其中，m为椭圆模板的短轴长.

1.2 系统照射方向

模板每旋转360°后将恢复为初始状态，着色图上的曲线则完成一个首尾相接的周期.由模板形状可知，其旋转0°～180°所得数据与旋转180°～360°所得数据相同，因此，只需要将探测物转过180°即可获得实验所需的所有数据.

设X射线与旋转中心和模板上小圆圆心连线之间所夹锐角为φ，则小圆圆心在探测器上投影点距起始点的距离l可表示为

l=l0+d0sinφ

(1)

式中：l0为旋转中心投影点到探测器起始点的距离；d0sinφ为旋转中心与圆心连线在探测器上的投影长度.

由式(1)可知，模板与探测器始端的距离可以表示为三角函数形式.而式(1)则为着色图中等宽曲线的数学描述，故可使用傅里叶级数拟合该曲线并求得其跨度q.由CT系统的工作原理可知，系统每次转过的角度相同，故探测器每次转过180°/q.

1.3 旋转中心标定

如图1b所示，C点对应等宽曲线的最高点，设θ1、θ2分别为A、C两点在坐标图上对应的横坐标，A、C两点的横轴间距θm为

θm=θ1-θ2

(2)

在实际情况下，θm与光线转过夹角相等，对应状态几何关系如图2所示.

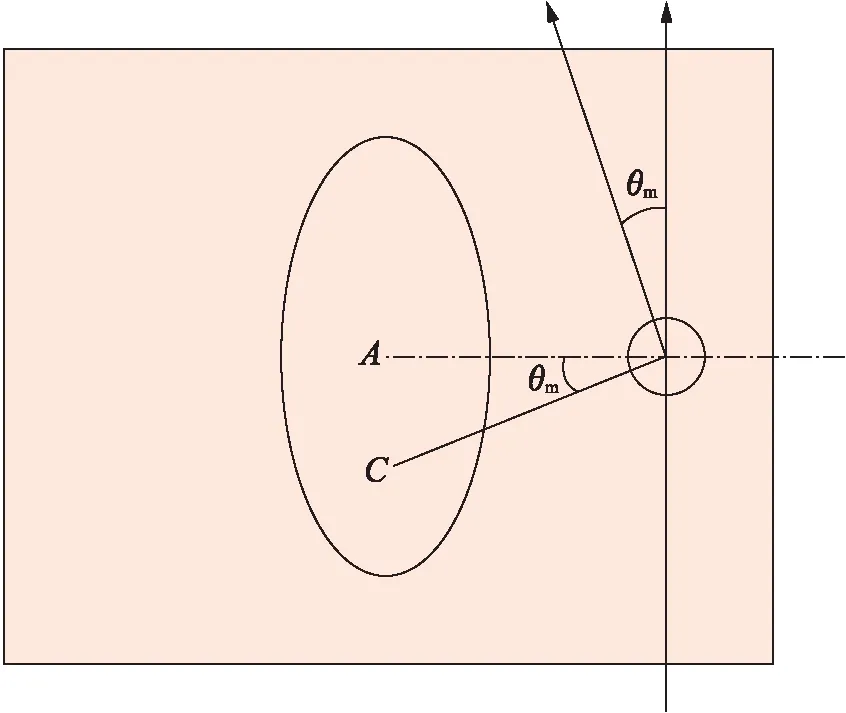
图2 A、C两点对应状态的几何关系Fig.2 Geometric relation of corresponding state between A and C points

由于探测器每次转过180°/q，故通过观察A、C两点之间对应列的列数I，即可求得

θm=I180°/q

(3)

当等宽曲线位于C点时，模板圆心与旋转中心的间距被完全投影到探测器上，表明此时圆心投影点距探测器始端最远；而当位于其对称位置时，距探测器始端最近.故只需计算出图1b中等宽曲线两极值点竖直方向上相差的单元格数目T，即可求出圆心与旋转中心之间的距离D，即

l(T-1)=2D

(4)

若以模板在图2的几何状态为基准，以左下角为原点建立直角坐标系，则旋转中心的坐标值表示为

(5)

2 模型CT成像伪影消除

CT图像断层平面中某一点的密度值可以看作平面内所有经过该点的射线投影值之和的均值.然而观测样品各点的形貌与吸收率各不相同，有些点比较突出，经卷积反投影处理后，这些点依旧突出，并可据此还原断层；但有些原本不为零的地方现在成为了零，即产生伪迹，因此，需要在反投影之前对投影进行滤波处理.

2.1 Radon变换及傅里叶变换

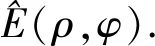
Pφ(ρ)=P(ρ，φ)

(6)

式中：w1、w2为傅里叶变换[15]的特征参量；F为傅里叶变换映射；P为投影函数p的傅里叶变换.可由傅里叶反变换求得待重建图像，即

a(x，y)=F-1[E(w1，w2)]=

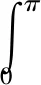
(7)

式中：α为实际某点投影角度；r为弧长.对于式(7)进行积分，可以整理为

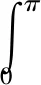
g[rcos(α-φ)，φ]

(8)

故待建图像转化为

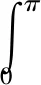
(9)

由前述推导过程可得

(10)

反投影得到托盘上各点的吸收率为

(11)

考虑到实际分析处理问题时需要将介质划分为256×256的微元格点研究，故需对上述连续模型进行离散化处理，则有

(12)

滤波因子采样得到

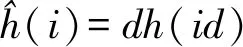
(13)

其取值为

(14)

可将离散条件下的反投影积分转化为级数求和，即

(15)

式中，N为一个微元满足的最小旋转角的最大倍数.将式(15)离散化则有

(16)

式中，Δx、Δy为横纵坐标最小变化量.

2.2 伪影消除

使用2.1节变换操作可确定绝大部分点的介质吸收率，然而，实际操作中发现有少部分点并没有X射线穿过而无法确定其吸收率[16].若使用近邻插值方法求取这些点的吸收率，虽仍能保持样品的形貌特征，但重建图像部分边缘较模糊，并形成伪迹.因此为抑制伪迹出现，一方面要对源数据进行降噪处理；另一方面需要对变换后的数据进行插值赋值，减小数据的偏离幅度.

本文使用3阶样条法对式(16)得到的重建图像进行插值处理.3阶样条法除了要求在两端与给定数据值相等外，还要求样条系统的光滑性，即内部邻接数据点的1阶及2阶导数必须匹配.在外侧端点1阶导数没有变化，2阶导数为零.样条函数定义为

(17)

其导数为

(18)

为满足数据匹配条件，则有

(19)

内部数据点1阶、2阶导数匹配，故在两函数衔接点gn(i2)处有

(20)

在外侧端点1阶导数没有变化，故2阶导数为0，即

(21)

联立式(18)～(21)可解得具体的插值函数，并可将[x1，x3]区间内任一点带入相应坐标求得其值.

3 算例分析

本文使用图1a所示的模板标定CT系统的参数，使用文中提出的方法求得探测器单元间距离l为0.280 4 mm，旋转中心的坐标为(58.633 1 mm，42.395 3 mm)，着色图中等宽曲线在整个数据点区间内跨度大约为180°，探测器每次转过1°，傅里叶变换特征参量w1、w2分别取30和60，滤波因子由式(14)求得.

使用标定后的系统参数进行测试实验，得到如图3所示的反投影结果.从图3可以看出，得到的重建图较为模糊，且轮廓周围泛有过渡白色.使用3阶样条法进行插值处理后得到的结果如图4所示，处理后的图像明显清晰，内部分布有两个彼此分离的椭圆空洞、两个相交的更高吸收率的椭圆形小区域.

图3 未经去噪、插值处理的图像Fig.3 Images without denoising and interpolating processes

图4 降噪、插值后样品最终图像Fig.4 Final image of sample after noise reduction and interpolation

本文也比较了消除伪影前后10个给定位置处的介质吸收率，如表1、2所示.根据表1结果可以看出，部分吸收率为负值，但其值均较小，表明实际吸收率应为0，存在一定的测量误差.比较表1、2的吸收率可知，消除伪影后能测得每个位置的吸收率，并能得到更清晰的重建图像.

表1 伪影消除前给定10个位置处吸收率Tab.1 Absorption rates at given 10 positions before artifact removal

表2 伪影消除后给定10个位置处吸收率Tab.2 Absorption rates at given 10 positions after artifact removal

3.1 算法精度分析

实验中的误差将降低测试精度，这些误差主要包括截断误差、公式化误差、舍入误差和测量误差.在参数标定时，本文讨论不涉及多项式近似，且忽略了次要条件的影响，并不会大幅度影响最终的结果.因此，本文算法的主要误差来源为给定实验数据、计算软件的舍入误差以及数据收集过程中不精确性引入的测量误差.下面以圆形遮光区域为例，推导吸光区尺寸与误差的定量关系.

设k为圆遮挡的X射线数，设z为真实值与测量值之间的偏差，则有

kd+z=2L

(22)

式中，2L为测量值，故相对误差为

(23)

由于一般情况下误差会控制在较小范围内，即kd≈2L，则有

(24)

由式(24)可知，随着物体半径L的增大，误差η在减小，表明增大模板吸光区半径，可有效减小误差.如将半径扩大为原来的二倍，则误差为

可见半径扩大为原来的二倍，误差几乎变为原来的1/2，因此，对于小圆半径相对于整个平板较小的情况，参数的测量精度还有较大的提升空间.但由于偏差z值较小，即使误差减半，也不会对最终结果影响过大，故本文测得的参数精度是可以接受的.

3.2 算法稳定性分析

本文假设X射线与椭圆中心、小圆圆心的连线恰好垂直，如图2所示.但实际上取样是非连续的，只能近似为垂直关系，由于探测器间距较近，这种近似导致的误差虽会随具体情况变化，但其值较小，在一定程度上是可接受的.

本文测试了以旋转中心坐标为例的参数值对系统参数的敏感性.将式(5)中的旋转中心横纵坐标对夹角θm求导，得到

(25)

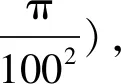
4 结 论

本文提出了一种基于卷积反投影算法的CT成像伪影消除方法.利用实物与投影的对应关系，根据投影方便、快捷地求出探测器间距等待系统参数；使用卷积反投影技术和三次样条插值算法，精确地求出每一点的吸收率并得到较清晰的重建图像.算例仿真测试的精确度、稳定性分析结果表明，提出的算法具有简明易懂、操作方便和精确度高等诸多优点，且其相较于传统方法具有更高的运算效率.