两自由度机械手臂的交叉耦合模糊逻辑控制*
2019-05-31郑伟勇李艳玮
郑伟勇, 李艳玮, 周 兵
(1. 河南工程学院 计算机学院, 郑州 451191; 2. 郑州大学 信息工程学院, 郑州 450052)
两自由度机械手臂在制造业、农业和建筑等领域有着广泛的应用[1-3],但任何一个系统都存在复杂的动力学特征,外部变化的干扰使得其辨识过程要比只存在内部变化的系统复杂得多,而对系统的辨识过程通常是以牺牲可靠性和精确度为代价的.因此,确定系统的动态变化和执行过程的自适应评估在实际应用中是非常有效的[4].控制问题必须考虑结构或非结构的不确定性、非线性以及控制目标,则解析设计域内的自由度必然减少,需要采用一定的适应性方法来解决上述难题.
根据操作人员的经验发展而来的模糊逻辑能够有效地抑制时变特性、噪声测量和建模动态等因素导致的不利影响[5].文献[6]关于模糊控制器的设计无法系统地解决系统鲁棒性不确定问题,存在一定的缺陷,现有的研究成果主要集中于模糊系统的改进;张小娟[7]改进了一种自适应神经模糊推理系统,其结构能够非常有效地提高模糊系统的实际性能,且输出是输入矢量的线性方程;Su等[8]基于Takagi-Sugeno模糊在线性系统模型空间内进行插值,充分利用传统设计方法的主要特征对相应的关键问题进行分析;文献[9]提出了参数化的模糊交集,在聚合规则的前提下提供一个自适应学习的可能性.
1 机械手臂建模
两自由度机械手臂通常采用液压驱动,运动主要为基轴和肩轴的转动,转动的角度直接决定机械手臂运动的轨迹,而该运动的精度则关系到机械手系统设计的性能指标.两自由度机械手的简化结构模型[10]如图1所示.

图1 两自由度机械手臂的简化结构模型Fig.1 Simplified structural model of mechanical arms with 2-DOF
首先需要建立两自由度机械手系统的动力学模型,其数学表达式为
M(θ)θ+C(θ,θ)θ+G(θ)=τ
(1)
(2)
式中:M(θ)、C(θ)、G(θ)和τ分别为状态变化惯量矩阵、哥氏力分量、重力分量和输入扭矩;I为转动惯量;S为动能;θ2为悬臂的旋转角度;m2为悬臂的质量;r1为基轴与立臂的距离.哥氏力可表示为
(3)
(4)
式中:hc1和hc2为势能;l2为悬臂长度;θ1为基轴的旋转角度.重力分量可表示为
(5)
式中:∂为偏微分符号;r2为肩轴转动半径.
考虑到液压缸的运动直接决定肩轴的转角,故需要建立相应的数学模型.根据机械手臂的通用模型可知,液压回路的动力学方程是非线性的,但液压缸和电动机的方程非常相似,通用数学表达式为
(6)
式中:pA和pB分别为两个液压缸内部的压力;AA和BB分别为液压缸活塞的面积;y为液压缸活塞位移;Fc为液压缸推力;Fμ为摩擦力;μ为输入信号的数值.
采用波长为550 nm的光作为入射光,在循环伏安特性曲线测试中即时记录光的透过率曲线,称为时间依赖性曲线(见图6,电解液为1 mol/L LiClO4).在电致变色薄膜中,将着色态/漂白态所表现的光透过率的低/高值标记为Tc/Tb.光的透过率差值ΔTλ=550 nm(Tb-Tc)是描述薄膜电致变色性能的一个重要指标(见图7(a)),随着循环伏安特性曲线测试的进行,ΔTλ=550 nm值有所衰减,这也表明了电致变色性能的衰退.通常,用电致变色效率η来衡量材料的电致变色性能,计算公式如下:
2 交叉耦合FLC控制器的设计
复杂伺服系统的数学模型难以获得的,因此,采用模糊控制器FLC对机械手臂进行控制,可以有效避免冗长的数学建模过程[11-12].此外,考虑到交叉耦合控制器对多自由度系统具有同步性高、稳定性好和收敛速度快等诸多优点,本文采用两个模糊逻辑控制器FLCθ1和FLCθ2分别对机械手的悬臂轴和立臂轴进行交叉耦合控制,并对立臂轴和悬臂轴输出转角的相对误差er进行交叉耦合反馈,控制流程如图2所示.其中,θ1和θ2分别为立臂轴和悬臂轴实际转过的角度,θ1R和θ2R分别为模糊逻辑控制器的输入值.
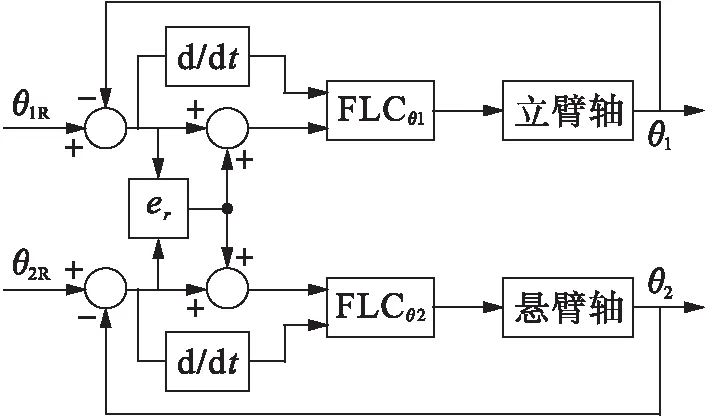
图2 交叉耦合两级模糊逻辑控制器流程图Fig.2 Flow chart of cross-coupled two stage fuzzy logic controller
本文采用一种交叉耦合两级模糊逻辑控制方法,主要特征在于相对误差分量的交叉耦合.对于该交叉耦合两级模糊系统来说,第j轴向子系统的模糊规则包括两个输入和一个输出,可通过“IF-THEN”的形式进行表述,即

第二级:IFUj1是AI3且erj是AI4,THENUj2是Bf2(I3,I4).
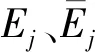
(7)
式中:k为第k个时间间隔;m为时间间隔的总数量.控制器设计的目的在于使误差状态趋近到系统的原点,为了求解性能指标Jj的最小值,推导其相对于erj和uj1的偏导数,即
(8)

(9)
根据最优控制原则,控制输入信号可表示为
(10)
式中,GUj为第二级控制系统的输出放大系数.定义fj2(erj,uj1)=-(|uj1|+uj1+|erj|+erj)/Δ.为了提升模糊系统性能,第二级系统的输出放大系数选择为GUj=cj|Ej|.同时,第二级系统的模糊规则生成函数可表示为
(11)


(12)
其中,round(x)为最接近于x的整数.由式(9)可知,大多数的负梯度-|jj|表明uj1是最大值,本文第一级系统采用uj1的正梯度,即
(13)
采用与上文类似的方法,第一级系统的输出可表示为
(14)
类似于第二级的规则生成方法,第一级系统的规则生成函数可表示为
(15)
交叉耦合模糊控制系统的模糊规则集合如表1、2所示.其中,第一列表示误差,第一行表示误差变化,中间为输出变量.提取方法主要以控制工程知识和成熟的控制经验为基础,以操作人员的实际控制过程为基础进行模型提取.
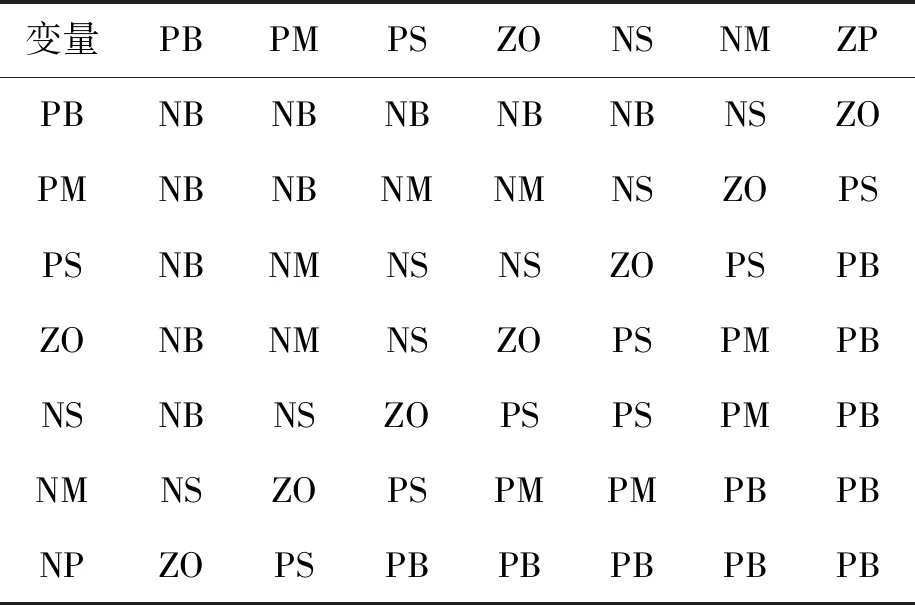
表1 子系统第二级模糊规则集合Tab.1 Fuzzy rule set at second stage of subsystem

表2 子系统第一级模糊规则集合Tab.2 Fuzzy rule set at first stage of subsystem
3 实验结果与分析
为了验证交叉耦合模糊控制器的有效性和可行性,利用MATLAB Simulink对设计的两自由度机械手臂控制器的阶跃响应进行数值模拟,并将其与传统PID控制器、基于遗传算法优化的PID控制器[14]的性能进行比较.
3.1 立臂和悬臂转角阶跃响应
两自由度机器人的基轴转角θ1和肩轴转角θ2分别设定为20°、40°和60°,图1中机械手臂的物理参数设定如表3所示.

表3 两自由度机器人的参数Tab.3 Parameters for robot with 2-DOF
采用传统PID控制器、基于遗传算法优化的PID控制器和交叉耦合模糊逻辑控制器对机械手臂两轴转角θ1和θ2的阶跃响应分别进行数值模拟,不同转动角度对应的阶跃响应特征分别如图3、4所示.
由图3、4可知,对于传统的PID控制器和基于遗传算法优化改进的控制器来说,基轴和肩轴的转角θ1和θ2的阶跃响应均存在明显震荡,且转动震荡的幅值随着预设稳定值的增大而增强,表明传统PID控制器会引起机械手臂运动的不稳定性,从而导致控制性能急剧恶化,并可能对机器人系统本身造成硬件损伤.其中,传统PID控制器对于θ1和θ2的阶跃响应分别存在约5%和12%的超调量,相对应的稳定时间分别约为0.1和0.15 s,这显然难以满足两自由度机械手臂对控制系统的性能要求.另外,基于遗传算法优化的PID控制器相较于传统PID控制器阶跃响应相对较小,同时对应的控制稳定时间相对较短.本文搭建的交叉耦合模糊逻辑控制系统对机械手臂基轴和肩轴转角θ1和θ2的阶跃响应均没有震荡和超调量,表明该控制系统具有优异的控制性能,非常有利于提高机械手臂的运动精度和稳定性.
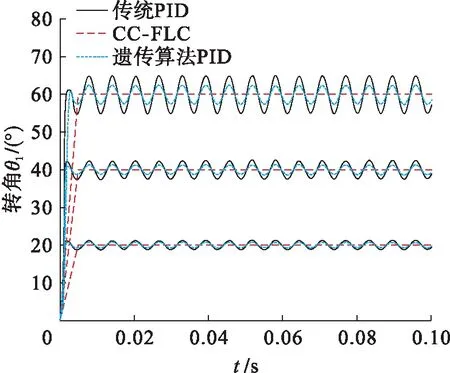
图3 不同控制器对转角θ1的阶跃响应Fig.3 Step response of angle θ1 with different controllers

图4 不同控制器对转角θ2的阶跃响应Fig.4 Step response of angle θ2 with different controllers
3.2 轨迹跟踪误差
根据以上三种控制器对不同大小转角的阶跃响应控制可以看出,转角θ1和θ2越大,相应的控制精度会降低,因此有必要对转角θ1和θ2的轨迹跟踪误差进行分析.选择θ1和θ2均为40°的转角作为分析对象,对比传统PID控制器、基于遗传算法优化的PID控制器以及本文的交叉耦合模糊控制器的转角误差曲线,结果如图5、6所示.
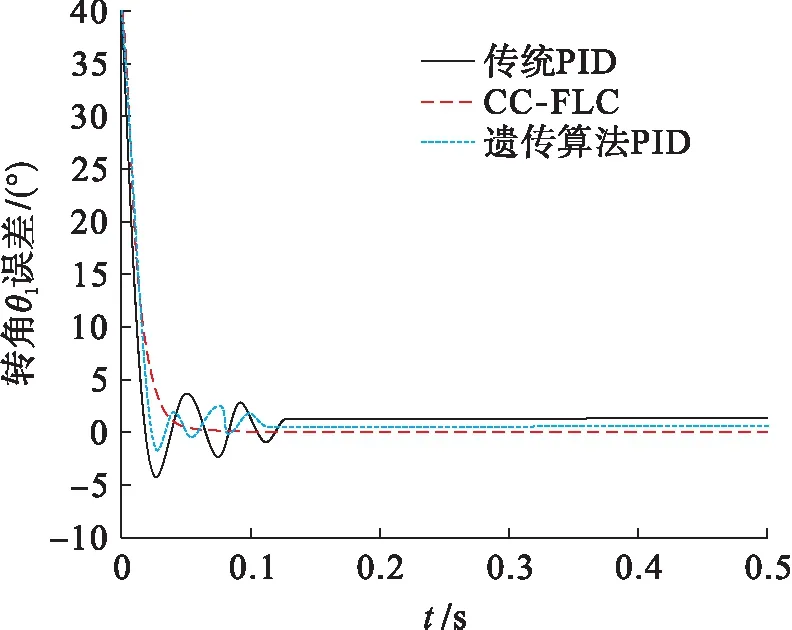
图5 三种控制器对转角θ1的跟踪误差曲线Fig.5 Tracking error curves of angle θ1 with 3 controllers

图6 三种控制器对转角θ2的跟踪误差曲线Fig.6 Tracking error curves of angle θ2 with 3 controllers
由图5、6可知,交叉耦合模糊控制器相较于其他两种控制器具有控制精度高和收敛速度快的特点.交叉耦合模糊逻辑控制系统对立臂转角θ1和悬臂转角θ2阶跃响应的稳定时间分别为0.05和0.12 s,明显优于传统PID控制器和遗传算法优化PID控制器.另外,传统PID控制器和基于遗传算法优化的PID控制器跟踪误差大致稳定在12%和8%,而交叉耦合模糊逻辑控制系统控制精度能够达到5%以下,使其能够完全满足两自由度机械手臂对其控制系统的性能要求.
4 结 论
针对两自由度机械手臂难以建立数学模型的问题,采用模糊逻辑控制方法设计了一种交叉耦合的两级控制系统,从而简化控制系统结构的复杂程度,避免机械手系统的非线性建模过程.利用MATLAB Simulink对设计的两自由度机械手臂控制器的阶跃响应进行数值模拟,并将其与传统PID控制器、基于遗传算法优化的PID控制器的性能进行仿真比较.仿真结果表明,交叉耦合模糊逻辑控制器的控制稳定性、超调量、响应速度和控制鲁棒性等性能均明显优于传统PID控制器以及基于遗传算法优化的PID控制器.
