基于EFDC模型的长江江苏段水流输运时间研究

王 文 才，杜 薇，范 中 亚，姜 龙，许 益 新，李 一 平

(1.河海大学 浅水湖泊综合治理与资源开发教育部重点实验室，江苏 南京 210098； 2.生态环境部 华南环境科学研究所，广东 广州 510655； 3.生态环境部 南京环境科学研究所，江苏 南京 210042)

水流输运的快慢及水体交换速率对于物质输移、水生生物生长、水体自净能力均有重要的意义[1-2]。目前研究水体输运时间尺度的内容主要包括冲刷时间、滞留时间、转化时间、通过时间和水龄等[3];研究手段主要包括水平衡[4]、示踪剂、拉格朗日粒子漂浮、放射性同位素[5]及数值模拟等方法[6-7]。其中水平衡方法虽然简单，但是不能很好地体现出空间上的水体动力情况；通过向水体投加示踪剂或者通过测定水体中放射性同位素的变化来得到水体滞留时间，也存在一定的空间和时间局限性。因此目前更多的是采用数值模拟的方式来研究河流[7]、湖泊水库[8-11]和河口海湾等各种特定地表水体的水流输运及水力滞留[6，12]。长江作为世界第三大河流，全长6 300多km，沿江经济相对发达[13]。下游长江三角洲更是中国经济最发达的地区之一，人口密度和工业化程度也相对较高，沿江大量生活污水和生产废水排放进入长江水体，造成水体中营养物质含量偏高，长江入海口及近海水体富营养化程度较高[14]，同时，沿江的化工厂也存在风险事故，存在危险化学品泄漏进入长江的可能。江苏地区作为下游相对发达的地区，大部分的污废水也都排放进入了长江。因此，研究长江江苏段的水流输运特点对于明确污染物输运及进行河段管理都具有重要的意义。本文基于EFDC模型中水龄和拉格朗日粒子追踪模块，采用设计流量和下边界潮位条件，研究长江江苏段的水流输运和水力滞留特点，在一定程度上阐明了长江江苏段的水流输运规律。

1 研究区域与研究方法

1.1 研究区域

本文以长江江苏段(主要是南京至徐六泾江段)为研究对象(图1)。长江下游大通以下为感潮江段，水位流速等水动力均受到长江入海口潮波向上传播的影响[15]，水动力过程较复杂。大通流量通常作为下游及入海径流量的依据[16-17]，长江南京至徐六泾江段位于长江下游，分布着南京、镇江、扬州、常州、无锡、苏州这6座城市，沿江包括南京、镇江、江阴、天生港和徐六径潮位站。

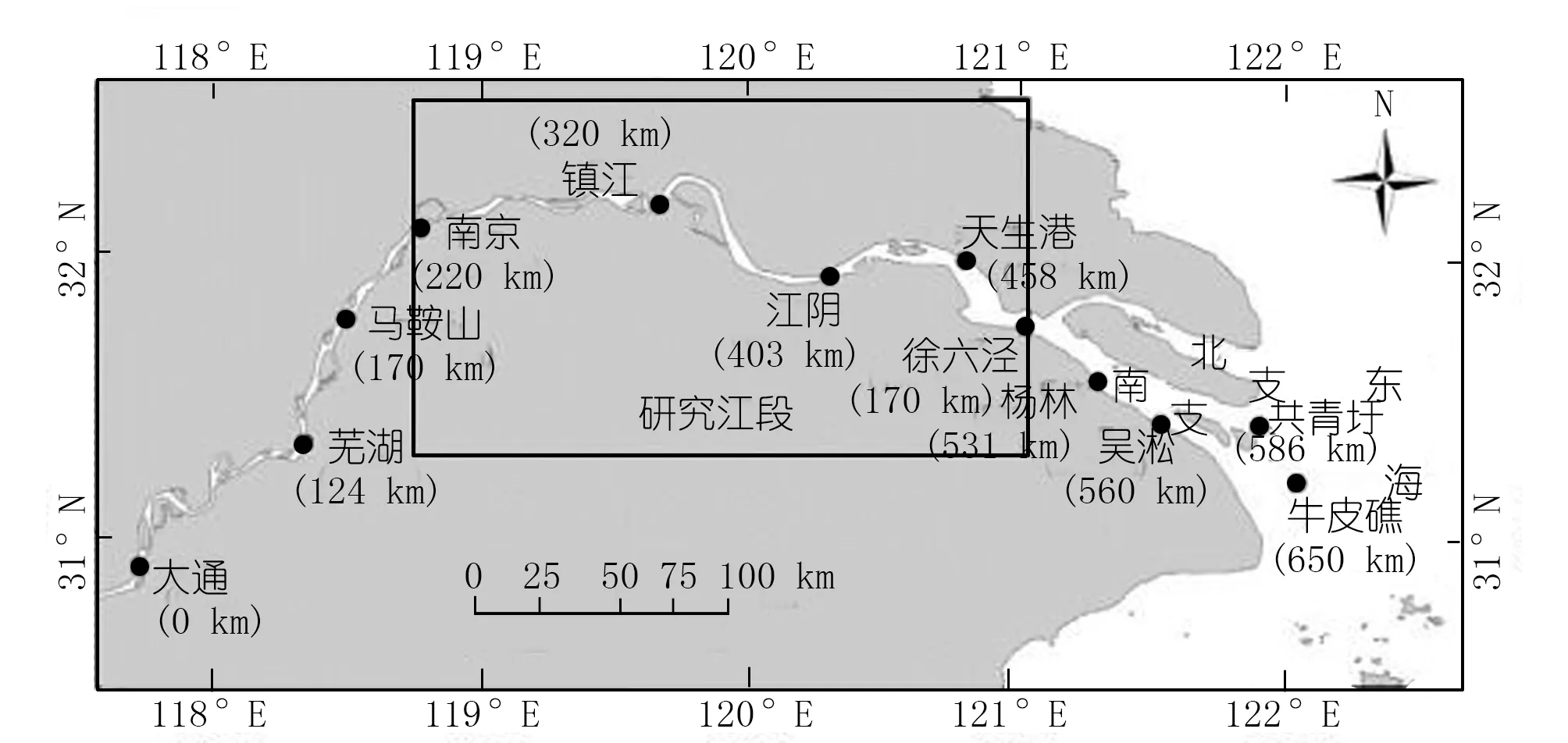
图1 研究区域 Fig.1 Study area

1.2 研究方法

1.2.1 模型建立

本研究选取可以用于模拟包括河流、湖泊、水库、河口、湿地、近岸等地表水体三维水流、物质输运和生物化学过程的模型系统EFDC。在用其构建长江南京至徐六泾江段的水动力模型的基础上，计算设计径流量和下游潮位下的江段水龄变化及拉格朗日粒子输移过程。

1.2.2 水龄计算方法

水龄的概念最早由Zimmerman提出[18]，定义为可溶性物质从入口传输到指定位置所需要的时间(通常将入口处的水龄设置为0)，可以反映水体的交换状况，水龄越大水体交换程度越弱。EFDC模型中水龄根据示踪剂来计算，水龄方程如下：

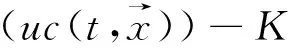
(1)

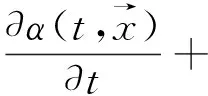
(2)

式中，c是示踪剂浓度，α是初始水龄浓度，u是时空分布的流速，K是扩散张量，t为时间。水龄α的计算如下

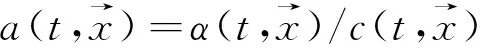
(3)

1.2.3 拉格朗日粒子追踪计算方法

拉格朗日粒子示踪剂模型(LPT)，可以模拟粒子在水体中的输移路径。该模型考虑了质量输运的对流扩散，三维曲线正交坐标系的质量运输对流扩散方程是：

(4)

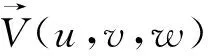
颗粒运动的微分方程与方程(4)一致，如下所示：

(5)

(6)

(7)

式中，dt是时间单元，p是一个由分布相同均值为0.5的随机变量产生的随机值。当转换使用2p-1时，这个随机部分的平均值为0并在-1～1范围内。变化的随机值允许扩散期限到更多颗粒+/-在平流运输方位。

为了判定颗粒的运动轨迹，方程都被纳入EFDC模型中。如上所述，数值求解方法分别被分为平流运输和随机成分。这个方法允许使用者开启和关闭水平或垂直方向的随机游走功能。微分方程可采用显式欧拉、预测校正欧拉和四阶龙格库塔方法来解。

1.3 研究方案

长江江苏段已开展过较多模型模拟应用，能够较好地模拟江段水动力状况。鉴于篇幅有限，此处不再赘述模型率定、验证结果。由于三峡工程的建设，下游大通水文站的极值流量发生了改变，洪峰流量降低，枯水流量变大。考虑三峡工程建设后2003～2013年最小流量和最大流量的范围，本研究江段模型上边界考虑10 000，20 000，30 000，40 000，50 000 m3/s和60 000 m3/s共6种设计流量；下边界徐六泾的潮位过程根据水文年鉴中逐日高、低潮潮位数据，采用cubic插值得到逐时的潮位，之后通过调和分析得到调和常数，最后得到设计潮位过程。采用EFDC模型进行模拟过程中，拉格朗日粒子释放时间设定在模拟开始后的0.5 d，在接近入口处随机释放20个粒子，通过模型计算得到各种设计情景下的江段水龄变化和拉格朗日粒子输移过程。

2 结果分析

2.1 不同径流量下长江江苏段水龄模拟

统一截取水龄达计算基本稳定、计算时间为第20 d的计算结果。不同径流量下模拟结果在空间上基本呈现相同的特征，因此此处只给出径流量为40 000 m3/s的结果(图2)，水龄值从上游向下游逐渐增大，入口处南京站所在位置的水龄为0。流量越大，水龄值的变化范围就越小。上游水龄在空间上分布相对均匀，下游接近出口徐六泾处水龄在空间上存在明显的变化，河道断面中间水龄小，靠近两岸的水龄大；另外，下游出口附近，受到下边界水流反向进入的影响，水龄的结果呈现出随时间波动较大的特征，甚至会存在水龄接近于零的区域。

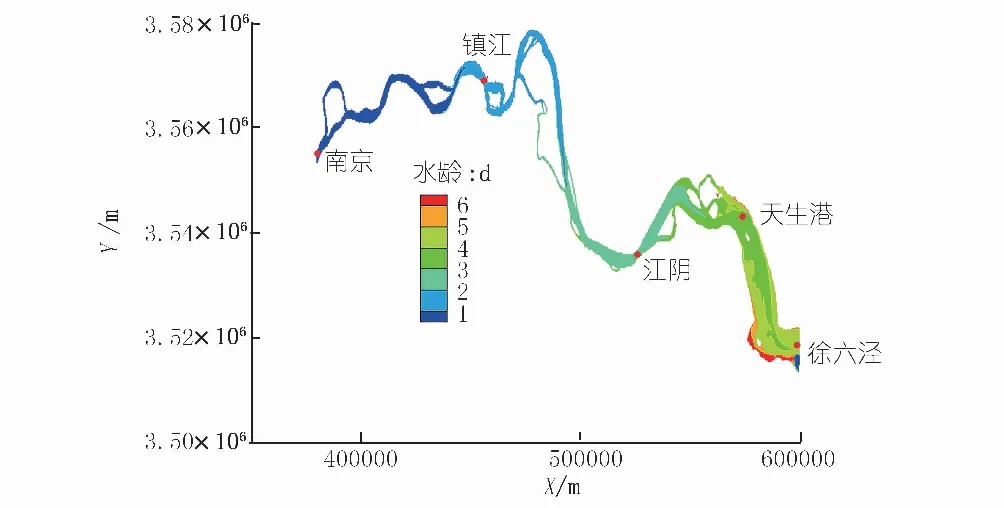
图2 流量为40 000 m3/s情况下江段水龄空间分布 Fig.2 Distribution of water age under the discharge of 40 000 m3/s

根据水龄计算结果，汇总在不同设计径流量下南京、镇江、江阴、天生港、徐六泾这5个代表性站点的水龄计算值见表1。

表1 设计流量下各站点水龄计算值

Tab.1 Water age of each station under designed discharge d

站点入口流量 10000 m3/s20000 m3/s30000 m3/s40000 m3/s50000 m3/s60000 m3/s南京000000镇江4.062.031.431.120.940.82江阴9.634.673.202.442.091.81天生港12.146.184.263.232.702.32徐六泾9.408.165.114.063.302.87

由于徐六泾的水龄值不稳定，以天生港为最下游分析，可以看到流量从10 000 m3/s增加到60 000 m3/s的情况下，天生港的水龄值从12.14 d减小到2.32 d，下降约80%，其它站点水龄值也存在大幅度下降趋势，这也就说明，丰水期和枯水期江段的水流输运时间存在较大的变化。

2.2 拉格朗日粒子输移结果

由于粒子是随机释放的，受河道断面上流速不均匀的影响，拉格朗日粒子的输移速率存在差异。本文中定义10%的粒子到达或通过某点为水流到达，90%的粒子通过或到达某点定义为水流完全通过。结合拉格朗日粒子的计算结果，以粒子到达和完全通过南京站的时间为第0 d，分别提取粒子到达和通过镇江、江阴、天生港及徐六泾的时间(表2)。从结果可以看出，粒子从到达各站点到完全通过需要一定的时间，越往下游所需要的时间就越长。流量从10 000 m3/s增大到60 000 m3/s，粒子从南京输移到镇江、江阴、天生港、徐六泾的时间范围分别为3.97～0.63，8.63～1.54，11.54～2.08 d和14.29～2.83 d。流量越小，输移所需要的时间越长；越往下游，流量的影响越大。粒子完全通过的时间也呈现出相同的特征。与此类似的是，粒子从到达到完全通过某个站点，所需的时间也会随流量的减小和离下游边界距离减小而变大。

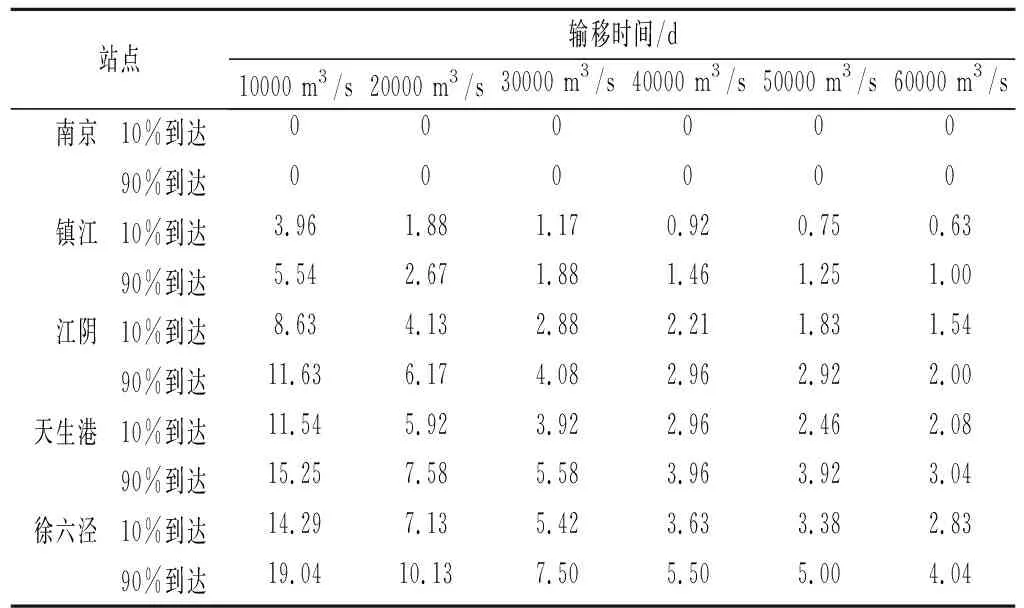
表2 不同流量下拉格朗日粒子从释放至到达相应站点的输移时间Tab.2 Transportation time of particle from relasee to arrival at corresponding site

3 讨 论

为分析水龄的沿程变化，以上游设计流量为40 000 m3/s为例，提取结果相对稳定的南京、镇江、江阴、天生港4个站点的水龄值和相应站点与南京的距离进行二次拟合(图3)，具有较高的拟合度。拟合函数的二次项系数为正，且从图3中也可以看出来，越往下游，相同距离所需要的输运时间也越长。河流中水流和粒子的输移总体上是从上游向下游，因此水龄总是沿河流向下游不断增大的。但是由于潮汐的原因，在长江下游潮流界内水流存在反向的特征，靠近下边界的部分存在开边界水向河段内倒灌的情况。因此越向下游的位置，水的输运速度越慢，相同距离输运所需要的时间也就越长。另外有关于长江口的水流输运时间的研究也表明在多年平均流量条件下，水流从徐六泾输运至河口大约需要24 d，说明下游段受到潮流的影响，水流输运会越来越慢[19]。其它有关感潮河流、河口的研究也都呈现类似的变化规律[6-7]。

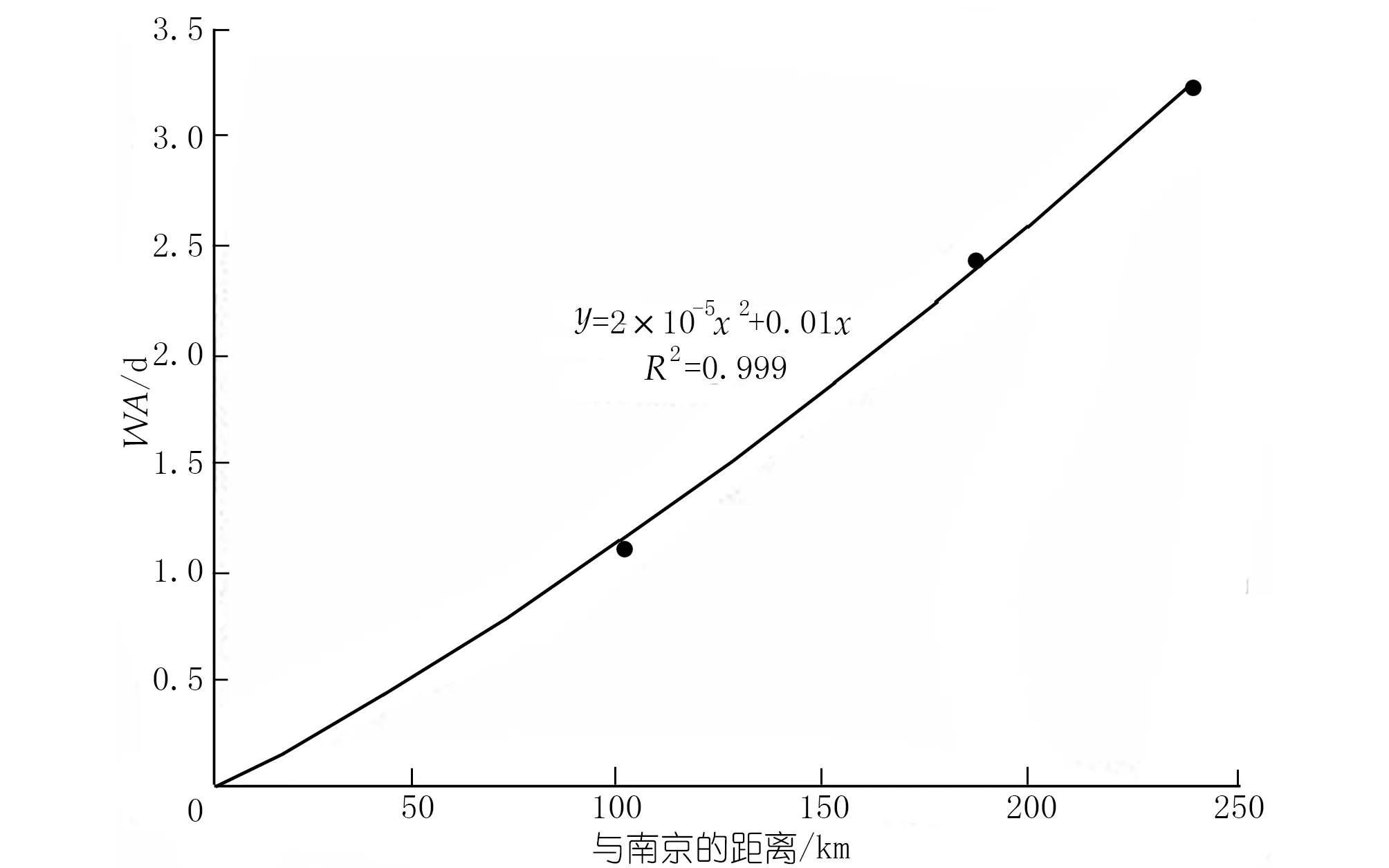
图3 40 000 m3/s径流条件下水龄的沿程变化Fig.3 Water age along the river under discharge of 40 000 m3/s

结合不同流量下各站点的水龄计算结果，采用幂函数对镇江、江阴、天生港3个站点稳定后的水龄和流量进行回归分析(图4)，R2均大于0.99，具有较好的拟合效果。随着流量的增大，水龄逐渐减小，但减小的幅度在下降。这与相关研究中采用指数函数对流量和滞留时间进行回归具有类似的效果[6,20]。在流量接近无穷大时，水龄接近0；而在流量接近0时，水龄接近无穷大，显然采用幂函数进行回归相比指数函数更符合实际。由于徐六泾位于模拟计算区域的下边界，在径流量较大情况下，随着径流量的增大，水龄的趋势与其他几个站点的趋势基本一致；但在径流量较小(Q=10 000m3/s)情况下，受下边界影响较大，与其径流量较大时的趋势并不一致。

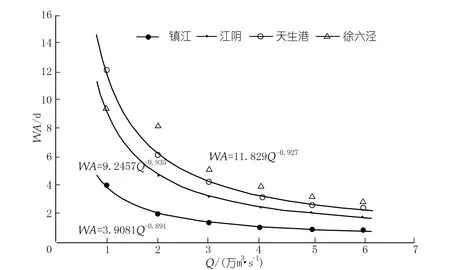
图4 各站点水龄与径流量的关系Fig.4 The relationship between water age and discharge at different stations

另外，拉格朗日粒子输移计算的结果呈现出与水龄类似的分布特征。采用幂函数来对粒子到达或通过各站点的时间与流量进行回归，同样能够表现出较好的拟合效果(见图5)。拉格朗日粒子示踪相比于水龄计算，在靠近下游开边界处更加稳定，不容易受到开边界水倒灌的影响。其中粒子到达站点的时间与水龄计算结果接近，粒子完全通过站点的时间则要相对较大，可以反映出污染物由于河流断面流速不均引起的粒子输移动态变化过程。以粒子完全通过和到达的时间为界，可以反映出类似的污染物经过相关站点所需要的时间。

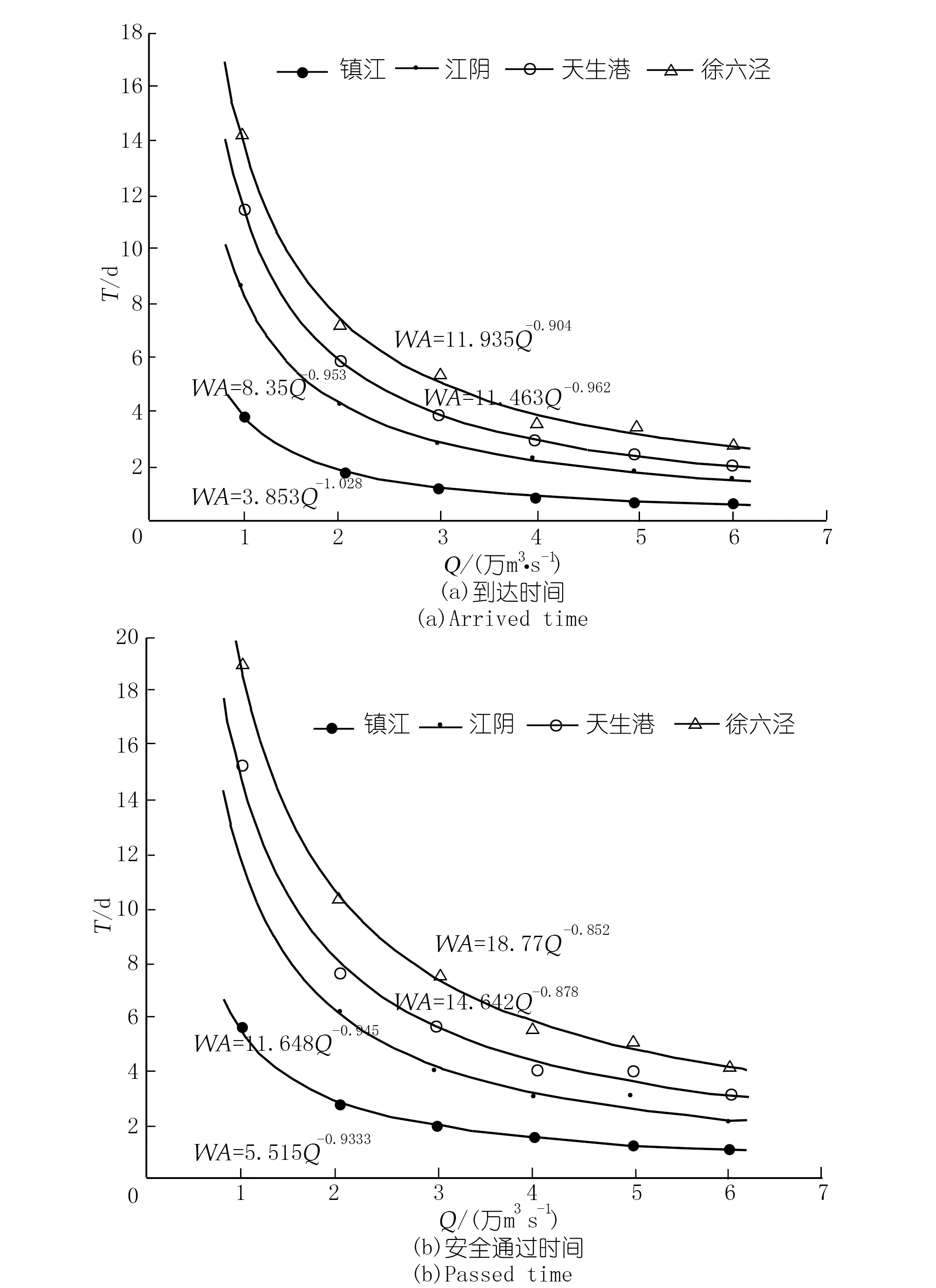
图5 设计流量条件下拉格朗日粒子到达和完全通过各站点的时间Fig.5 Time duration of particle arrived and passed the specific station under the designed discharge

4 结 论

本研究基于EFDC中的水龄和拉格朗日粒子示踪模块，以长江江苏段(南京至徐六泾)为研究对象，模拟了不同设计流量及下边界潮位条件下的江段水龄分布及拉格朗日粒子输移时间的规律，研究结果表明：

(1) 受下游潮汐的影响，越靠近下游水体输运越慢，水流输运相同的距离所需要的时间也相对越长。

(2) 河段整体的水流输运时间与径流量呈现非线性关系，在流量相对较小时水流输运受流量的影响较大。

(3) 拉格朗日粒子示踪的方法相较于水龄计算的方法，在河段下游的水流输运结果的稳定性受开边界水位影响更小。

(4) 水流沿程的输运时间与径流量可以采用二项式进行拟合描述。水流从入口输运到达、完全通过特定站点以及该站点的水龄均可以采用幂函数进行回归计算，均有较好的效果。

本研究可以为突发性污染事故的预警以及河段管理提供支撑。