斯特林机活塞杆帽式组合密封动密封性能分析*

2

(1.兰州理工大学机电工程学院 甘肃兰州 730050; 2.兰州理工大学温州泵阀工程研究院 浙江温州 325000)

斯特林发动机活塞杆的密封性能，是斯特林发动机的关键技术之一。随着密封工作压力和温度的提高，密封件从常规的单件密封(如O形密封圈)发展到滑环式组合密封，并相继出现了对称滑环式组合密封(如格莱圈)、非对称滑环式组合密封(如斯特封)和C形对称滑环式组合密封等。针对斯特林发动机苛刻的运行工况，为了提高斯特林机的密封性能，杨东亚、CHANG等[1-2]针对活塞杆动密封结构的特点，设计了一种新型的使用填充PTFE制成的帽式组合式活塞杆密封结构，使斯特林机的密封性能得以提升。帽式密封环在运动磨损后，O形圈提供的弹力能够使帽式密封环产生足够的弹性变形而始终贴合活塞杆配磨表面，以补偿一定的磨损量，从而延长有效密封时间。因此，帽式密封在无油干摩擦工况下具有普通滑环式组合密封所不具备的动态磨损和动态补偿功能。

目前，研究人员采用有限元模拟方法对组合密封的结构、特点和密封机制进行了深入研究。纪军和阎宏伟[3]利用ANSYS建立FESCO气缸O形密封圈二维轴对称模型，对不同结构参数下密封圈的静态和动态密封特性进行研究，并就O形密封圈进行简单温度场分析。张欢等人[4]利用软件Abaqus进行了DAS组合密封静特性的分析研究。刘清友等[5]运用Abaqus软件建立了C形滑环式组合密封的有限元模型，并从二维轴对称结构上对其密封性能进行分析。张甜等人[6]利用有限元软件ANSYS/LS-DYNA，分析了不同安装条件下活塞杆和密封圈接触面上接触应力的分布情况，并结合实验得到了帽式密封较优的安装使用条件。

以上对组合密封结构、特点以及密封机制的研究，主要集中在静密封特性研究方面，没有对组合密封的动密封进行深入研究，缺少动态温度场模拟分析，尤其是对无油干摩擦下组合密封的热力耦合研究甚少。本文作者运用Abaqus建立帽式密封二维轴对称有限元模型，模拟帽式密封实际工况，从静态和动态2个方面研究了密封工质压力对帽式密封性能的影响；同时从热力耦合角度分析了各因素对动密封性能的影响，为帽式密封结构的设计和优化提供理论基础。

1 密封机制

斯特林机活塞杆无油润滑帽式密封是由帽式密封环、O形圈和挡圈组成的组合式密封结构，如图1所示。该密封结构利用活塞杆与帽式环间过盈配合和O形圈挤压变形产生弹性力，使活塞杆和密封环紧密贴合来实现密封。同时，O形圈变形弹力挤压帽式密封环变形使其紧贴活塞杆，可以补偿活塞杆往复运动与帽式环相互摩擦产生的磨损量，从而延长可靠的密封周期，使密封更加有效。另外，帽式密封环由低摩擦、自润滑的改性材料填充PTFE制成，符合无油润滑干摩擦的特殊工况，合适的配比制成的改性材料使得摩擦力大大降低。此外，其帽式密封环的结构还可消除O形密封圈的拧断和挤出事故，使得帽式动密封工作寿命比普通橡胶密封制品高8～10倍[7]。因此，帽式密封动态补偿的结构，能有效防止工质泄漏，对提高斯特林发动机密封性能具有重要作用。

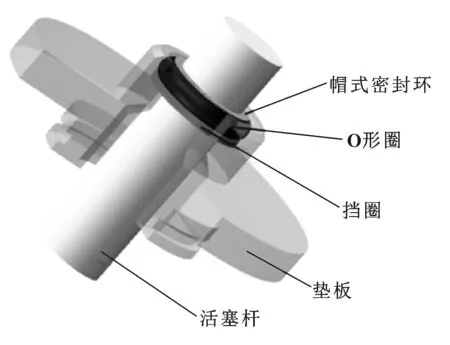
图1 帽式组合密封

2 模型构建

2.1 基本假设

研究所用O形圈是超弹性材料丁腈橡胶，具有几何非线性、材料非线性与接触非线性的特点。在有限元分析过程中，假设[8]：

(1)材料的泊松比和弹性模量是一定的；

(2)蠕变不会造成体积变化，橡胶材料的拉伸与压缩蠕变性质一致；

(3)约束边界的指定位移是造成橡胶密封圈的纵向压缩。

2.2 橡胶材料本构模型

Mooney-Rivlin本构模型通常用于描述变形小于30%的超弹性材料，O形圈是超弹性体，由应变能函数来表示。其函数表达式[9]如下：

W=C10(I1-3)+C01(I2-3)

(1)

式中：W为应变能密度；C10和C01为材料Mooney-Rivlin模型系数；I1和I2为第一、第二应变张量不变量。

O形圈的材料为丁腈橡胶，IRHD硬度为85。由于常数实际测量困难，应用时仅取部分项作近似计算[10-12]。文中使用的常数是通过经验公式(2)和(3)计算而来：

C10=E/(6×1.25)≈1.87(MPa)

(2)

C01=0.25C10≈0.47(MPa)

(3)

2.3 温度场分析理论

活塞杆在无油润滑的系统工况下往复运动时，温度对其密封性能的影响较大，活塞杆工作表面和滑环密封表面之间的相互滑动摩擦而产生热量，且在斯特林机闭式热循环系统中，摩擦生热对帽式密封环的影响大于系统热循环温度对密封环的影响。这些热是以扩散形式分别进入两摩擦副，不失其意义的前提下，为了使问题更易于处理，作出以下假设：

(1)忽略因热辐射导致的热损失，忽略泄漏所带走的摩擦热；

(2)认为各层材料的性质参数皆属各向同性；

(3)与整体摩擦热相比，相互滑动产生的微小磨屑带走的热量很小，可忽略不计；

(4)试样的四周产生对流换热，故试样的空间位置及温度分布与换热系数的选取无关；

(5)温度的变化对摩擦副材料的密度影响较小， 忽略密度随温度的变化。

根据上述假设，基于能量守恒原理，将密封环的传热问题简化为二维问题。瞬态传热[13]可用公式表达为

[C]{Tζ}+[K]{T}={Q}

(4)

式中：[C]为比热容矩阵；{Tξ}为温度对时间的倒数；[K]为传导矩阵，包含导热系数、对流系数以及辐射率和形状系数；{Q}为节点热流率向量，包含热生成；{T}为节点温度向量。

使用热通量密度来表示接触摩擦产生的温度变化。在特定的传热过程中，材料的边界条件和性能等会随温度发生变化，此类问题属于非线性热分析。Abaqus滑动接触热分析中，热通量密度计算公式为

q=kτv

(5)

式中：k为摩擦热的能量转化因子；τ为接触摩擦应力；v为活塞杆的滑动速度。

在获得整个结构场的结果后，利用Abaqus首先提取接触摩擦应力τ，代入已知的活塞杆滑动速度v，导入系数k=0.256，通过式(5)计算出热通量q；同时再利用Abaqus进行摩擦接触属性定义中，设定接触作用方式为切向行为，并使用各向同性的罚单元摩擦公式，采用与温度有关的摩擦因数，生热接触属性中，有摩擦产生的耗能百分比为100%，表面换热率为0.058，对仿真结果分析中提取节点应变。

2.4 基于Abaqus的帽式密封有限元模型

当对帽式组合密封进行有限元分析时，基于组合密封结构的几何形状、材料、边界条件，可将整个帽式密封结构简化为二维轴对称模型，从而在保证计算结果准确性的前提下，提高计算速度，节省分析时间。在数学建模的过程中，密封系统的结构、边界条件、约束条件以及作用载荷都呈轴对称分布，在载荷作用下模型的应力、应变和位移也呈轴对称分布，因此，可将模型的力变形计算简化为轴对称分析问题。轴对称问题的平衡微分方程为

∂σr∂γ+∂τrz∂z+σr-σθr+gr=0

∂τzr∂r+∂σz∂z+τrzr+gz=0

(6)

轴对称问题的物理方程为

{σr=E(1-μ)(1+μ)(1-2μ)[εr+μ1-μ)εθ+εZ)]

σθ=E(1-μ)(1+μ)(1-2μ)[εθ+μ1-μ)εr+εZ)]

σz=E(1-μ)(1+μ)(1-2μ)[εz+μ1-μ)εθ+εr)]

τzr=E2(1+μ)γzr

(7)

式中：σr、σθ、σz和τzr为应力分量；εr、εθ、εz和γrz为应变分量；gr、gz为单位体积的体积力分量；E、μ分别为弹性模量和泊松比。

活塞垫板和活塞杆采用对称且规则的几何单元，材料为18GrMnTi，泊松比为0.3。活塞杆采用四节点轴对称热耦合四边形单元CAX4HT进行网格划分，活塞垫板采用四节点双线性轴对称四边形单元CAX4R进行网格划分。活塞垫板的弹性模量为209 GPa，远高于与其相互作用的丁腈橡胶O形圈，故可将活塞垫板视为刚体。为方便分析，挡圈亦可视为刚体。帽式密封环的材料为改性的PTFE材料[14-15]，采用四节点轴对称热耦合四边形单元CAX4HT进行网格划分。PTFE弹性模量为960 MPa，泊松比为0.4。采用轴对称的方式对模型进行求解，应用自由网格重划分技术建立了如图2所示的有限元模型。

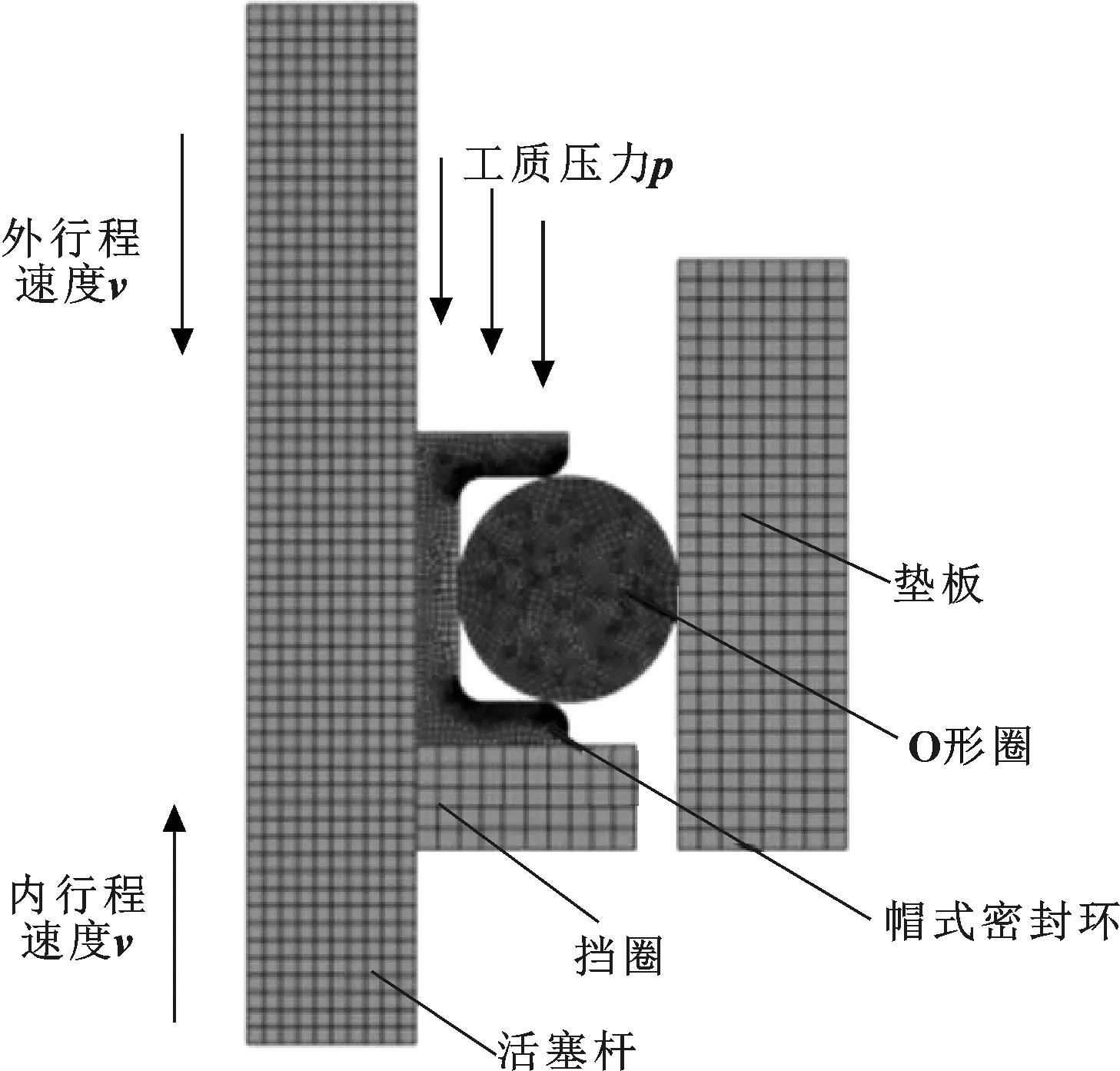
图2 组合密封有限元模型

在模型中定义了3个载荷分析步：

(1) 对帽式组合密封系统中的活塞垫板施加一段位移，产生一个预压缩应力，模拟帽式密封在过盈配合过程中的应力应变情况；

(2) 将工作压力施加到帽式密封环和O形密封圈与工质气体接触的一侧；

(3) 在活塞杆上施加一个按照y=Bsinϖt往复运动的速度载荷，模拟密封环的相对滑动过程，并对帽式密封的温度场进行稳态与瞬态热分析。

在实际接触过程中，定义了密封环和活塞杆、密封环与O形圈以及O形圈与活塞垫板3个接触对。在进行结构-热耦合分析时，首先基于系统最初模型进行结构分析，再在此基础上进行温度场分析。在整个帽式密封环的温度场稳态分析中，固定周围环境温度，不考虑热辐射产生的热流传导。在动态密封分析中，采用热耦合瞬态分析，即当活塞杆以一定速度往复运动时摩擦热随时间变化的过程。

3 工质压力对帽式密封的影响

帽式密封作为防止气体工质泄漏的无油干摩擦密封结构，工质压力是其主要的影响因素。根据密封理论与力的平衡原理，当2个密封摩擦副表面间的接触应力不小于工质压力时，可以保证密封系统的密封效果。下文将以工质压力为变量，结合预压缩量来分析帽式密封的静、动态密封性能。

3.1 工质压力影响的静态分析

在密封的静态分析中，凭借装配过盈量或预加载荷压缩具有弹性的橡胶体来实现初始密封。工作过程中，工质压力作用在密封圈暴露于介质的表面，进一步压缩密封圈，使得密封面间的接触压力增加进而实现“自密封”。在预压缩量为0.4 mm，过盈量为0.1 mm的初始安装下，分析不同压力下O形圈和帽式密封环的Von Mises应力分布，分别如图3和图4所示。

图3 不同压力下O形圈的Von Mises应力分布

图4 不同压力下帽式密封环的Von Mises应力分布

由图3、4可知：O形圈和帽式密封环的Von Mises应力随工质压力的增加而增加；O形圈的最大Von Mises应力位于与帽式密封环下环端接触的部位；帽式密封环的最大Von Mises应力集中在帽式密封环内部上环口，其大小受工质压力的影响很大，因此帽式密封环内部上环口处应做倒角处理。

图5示出了不同压力下活塞杆与帽式密封环间的接触应力分布情况。压力为1 MPa时在0～0.25 mm和1.25～2.5 mm处实现有效密封，这与初始静密封时的预压缩率有关，最大接触应力为7.3 MPa，能保证有效密封。在大于1 MPa的压力工况下，有效密封区域主要集中在1.25～2.5 mm处，其最大接触应力均大于工质压力，能保证有效的密封条件，压力越高，密封有效区越大。

图5 不同压力下活塞杆与帽式密封环间的接触应力分布

3.2 工质压力影响的动态分析

活塞杆做往复运动，可将其运动过程分为外行程和内行程，与气体工质压力方向相同的为外行程，相反的为内行程。基于压力对密封的静态影响分析，在预压缩量为0.4 mm，活塞杆过盈量为0.1 mm，工质压力为5 MPa，活塞杆速度为1 m/s时，某时刻外行程和内行程时的O形圈和帽式密封环Von Mises应力分布分别如图6、7所示。

如图6、7所示，在相同工况条件下，帽式密封环的最大Von Mises应力外行程时大于内行程，而O形圈的最大Von Mises应力变化不大，这与其动密封运行工况和材料特性有关。

图6 不同工况下帽式密封环Von Mises应力云图(t=0.3 s)

图7 不同工况下O形圈Von Mises应力云图

图8示出了工质压力5 MPa下活塞杆与帽式密封环间的接触应力分布。可见，在相同压力下，活塞杆与帽式密封环间的接触应力在外行程时有效密封区域比内行程时大。图9示出了活塞杆与帽式密封环间最大接触应力随工作压力的变化。可见，最大接触应力随工质压力的增大而增大，且内行程接触应力略小于外行程时的接触应力。因此，为保证更有效的密封性能，应保证内行程时的有效接触应力大于相应的工质压力。

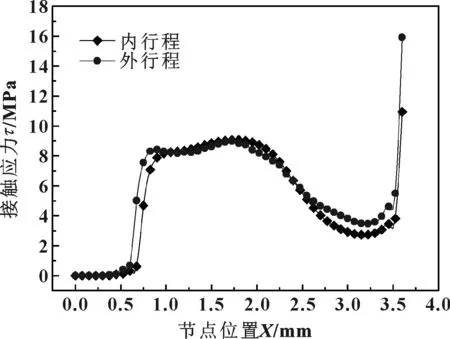
图8 工质压力5 MPa下活塞杆与帽式密封环间的接触 应力分布

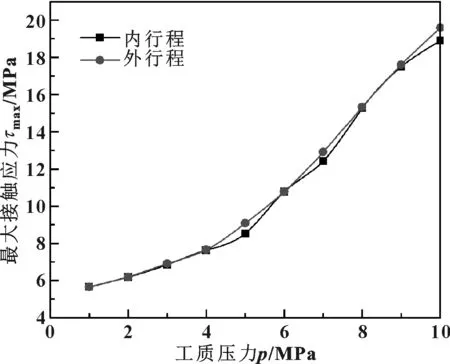
图9 活塞杆与帽式密封环间最大接触应力随工作压力的变化

4 基于摩擦热的影响因素分析

根据摩擦热计算公式Q=μFv，摩擦热Q与摩擦因数μ、正压力F以及摩擦运动速度v有关。

4.1 环境温度影响力分析

根据工程实践中斯特林发动机实际运行工况，在初始温度为20 ℃，密封与压缩量为0.4 mm，活塞杆滑动速度为1 m/s，摩擦因数为0.2，工质压力为5 MPa下，模拟斯特林发动机冷启动、热运行、热停止运行过程的温度场分布。图10示出了在不同环境温度下稳定运行2.5 min的温度场分布。

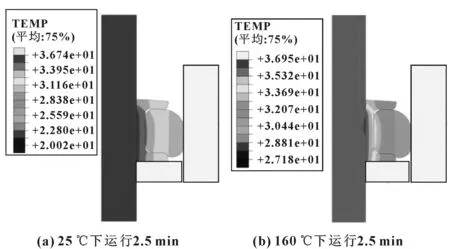
图10 不同环境温度下稳定运行2.5 min的温度场分布

通过图10(a)和(b)的对比分析，再结合斯特林发动机实际运行工况，可知在相同工况条件下，不同环境温度对帽式密封温度场分布的影响不明显，而活塞杆往复运动摩擦生热引起的温升较快，对其热机效率和热平衡影响也较大。因此，在相同工况下活塞杆摩擦生热对帽式密封温度场分布的影响较大，而环境温度对其温度场分布影响不大。下文选择斯特林机正常运行的温度160 ℃来对帽式组合密封的温度场做进一步分析。

4.2 温度场瞬态分析

针对斯特林发动机使用工况，在往复运动速度为1 m/s，摩擦因数为0.2，工质压力为5 MPa，初始温度为20 ℃，环境温度为160 ℃时，分析不同时刻帽式密封的瞬态温度场分布，如图11所示。在此工况下，不同时刻帽式密封环与活塞杆间的接触应力分布如图12所示。

图11 不同时刻帽式密封瞬态温度场分布

图12 不同时刻帽式密封环与活塞杆间的接触应力分布

如图11所示，在初始温度为20 ℃，环境温度为160 ℃时，活塞杆运行15 min后完全达到热平衡状态，活塞杆与帽式密封环实现热平衡稳定磨损。如图12所示，在5 MPa的压力下，随着活塞杆运动时间的增加，有效接触密封区域减小，最大接触应力相差不大，为探究最极端的密封条件，应考虑15 min或者更长运行时间下，热力耦合因素对动密封性能的影响。

4.3 摩擦因数的影响力分析

基于斯特林发动机实际运行的工况条件，在预压缩量为0.4 mm，活塞杆运动速度为1 m/s，环境温度为160 ℃，运行时间为15 min时，分析不同摩擦因数对帽式密封性能的影响，结果如图13和图14所示。

图13 不同压力下帽式密封环最大Von Mises应力随摩擦 因数的变化

图14 不同压力下活塞杆与帽式密封环间最大接触应力随摩擦 因数的变化

从图13中可以看出：不同压力下帽式密封环的最大Von Mises应力变化规律相似，其外行程时最大Von Mises应力随着摩擦因数的增大而增大，内行程时最大Von Mises应力随着摩擦因数的增大而略有减小，且工质压力越高变化趋势越明显。

从图14可以看出：活塞杆与帽式密封环间外行程最大接触应力随摩擦因数的增大而增大，内行程最大接触应力随着摩擦因数的增大而减小，且内行程最大接触应力小于外行程最大接触应力；不同工质压力下的变化趋势类似，压力越大变化越明显。根据力平衡条件，为了保证可靠的密封，最大接触应力的最小值应始终大于工质压力，因而应主要考虑不同摩擦因数下内行程的最大接触应力。由于内行程中的最大接触应力随摩擦因数的增大而减小，为了获得内行程相对较大的最大接触应力，摩擦因数越小越好。同时摩擦因数越小，对帽式密封环的磨损相对较少，最大Von Mises应力较小，有益于在可靠密封的条件下延长其使用寿命。

4.4 速度的影响力分析

在温度场热力耦合分析中，活塞杆往复运动速度直接影响着摩擦热的产生。在预压缩量为0.4 mm，摩擦因数为0.2时，在不同压力和活塞杆运动速度下对帽式密封性能进行分析。图15所示为不同压力下帽式密封环最大Von Mises应力随活塞杆运动速度的变化，图16所示为不同压力下活塞杆与帽式密封环间最大接触应力随活塞杆运动速度的变化。

从图15、16可知，活塞杆往复运动速度在0.5～2.5 m/s变化时，最大接触应力和最大Von Mises应力整体变化较小，且总体外行程时的变化幅度比内行程时大，这是由于流体压力方向波动变化引起的。外行程接触应力明显大于内行程，说明密封性能良好，不会发生泄漏。

图15 不同压力下帽式密封环最大Von Mises应力随活 塞杆运动速度的变化

图16 不同压力下活塞杆与帽式密封环间最大接触应力随活 塞杆运动速度的变化

图15、16的结果表明，运动速度对帽式密封环接触应力影响不大，但运动速度越快，摩擦力作用下的摩擦生热会加快，导致密封件的磨损加剧，使用寿命缩短。因此，活塞杆运动速度也是设计密封时要着重考虑的因素。

5 结论

(1)密封静态分析结果表明，工质压力对密封性能的影响较大，帽式密封环的最大Von Mises应力和最大接触应力随工质压力增大而增大，有效密封区域主要集中在帽式密封环1.25～2.5 mm处，压力越高，密封有效接触区越大。

(2)密封动态分析结果表明，帽式密封环间的最大接触应力随着工质压力的增大而增大，且外行程的接触应力略大于内行程。因此，为保证更好的密封性能，应首先使内行程的有效接触应力大于工质压力。

(3)环境温度对帽式密封温度场分布影响不大，帽式密封的热源主要来自摩擦热，在活塞杆运行15 min后达到稳定热平衡态。随着活塞杆运行时间的增加，有效接触密封区减小，这是由于磨损引起的，但最大接触应力变化不大，在一定动态自补偿范围内可以保证有效密封。

(4)针对摩擦因数的热力耦合分析表明，外行程时最大Von Mises应力和最大接触应力都随摩擦因数的增大而增大，内行程时随摩擦因数的增大而略有减小，且内行程最大接触应力小于外行程，因此，要着重考虑内行程的最大接触应力。为了得到相对较大的内行程最大接触应力，摩擦因数越小越好，这样Von Mises应力相对较小，磨损和摩擦生热也较少，有益于在可靠密封的条件下延长使用寿命。

(5)针对运动速度的热力耦合表明，运动速度对帽式密封环的接触应力影响不大。但运动速度越大，在摩擦力作用下，摩擦热加剧，密封磨损加快，使用寿命缩短。因此，活塞杆无油润滑下的运动速度也是密封设计要考虑的重要因素之一。