问渠那得清如许 为有源头活水来——核心素养在教学中的体现

☉湖北省武穴市教育科学研究院 刘全丰

☉湖北省武穴市育才高中 吴加兴

随着2016年“中国学生发展核心素养”的正式诞生，高中数学课程标准修订组还将“核心素养”与数学课程相结合，“核心素养”在数学教学及研究中迅速走红，它包括：数学抽象、逻辑推理、数学建模、直观想象、数学运算和数据分析这六大素养.在2019年的高考大纲中又增添了“新生思想道德素质”“促进学生德智体美劳全面发展”等表述，这实际上反映了教育要回归到教育的本源问题：培养人的活动.在近几年，数学核心素养就渗透到了数学教学的方方面面.现在就概率统计中的某些问题来谈谈核心素养是如何体现的.

例1某地区对垃圾进行无害化处理，从2008年至2014年的处理量（单位：亿吨）的折线图如图1：

图1

（Ⅰ）由折线图看出，y与t的关系可以用线性回归模型拟合，请用相关系数加以证明；

（Ⅱ）（略）

参考数据

参考公式：相关系数

回归方程yˆ=aˆ+bˆt中斜率和截距的最小二乘估计公式分别为：

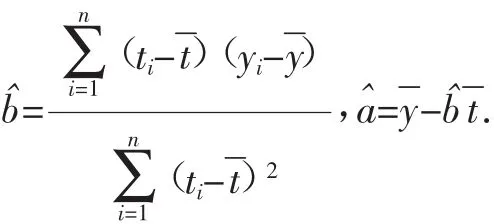
分析：这道题目是一道统计题目，它首先通过对某地区2008年至2014年垃圾无害化处理量的数据进行收集，画出其散点图，然后通过数学直观，抽象出它有可能是一个线性回归模型，但是它是否符合线性回归模型？我们通过计算相关系数r（数学运算），得到r≈0.99，r＞0.75，r→1，通过对数据的分析，我们知道可以用回归直线来模拟，从而达到建模的目的，它实际上是数学六个核心素养的一个整体应用.

在计算线性相关系数时，虽然是阅读材料，但是它告诉了我们线性相关系数的公式，只需要把数据直接代入即可求解，所以这应该是一道简单的计算题.

但是，现实情况却出人意料，很多学生看到这道题目时却傻眼了，大部分学生无从入手.他们发现：题目中的参考数据中并没有现成的数据可以直接代入，结果只能让这些分数白白丢失.究其原因，无非就是不能用条件中的参考数据来表示.即使是能够得分的部分同学有的也是死记结论来得到的，所以是极不可靠的.这道题的命题意图实际上是要求学生能够通过数学运算和逻辑推理来得到这两组公式间的相互转换：

这个问题在很大程度上反映了我们教学中存在的问题：忽视了每个概念、定义、公式、性质等内容的推导过程，在课堂上迅速地把这些内容摆出来，讲例题，套公式，然后通过大量的习题，使学生达到掌握的程度.但是这种学习非常的费时、费力，而且学生不懂得变通，对于平时没有见过的问题就会束手无策.同时在近几年高考中增加了概率统计的难度和地位：从过去的“送分”题，到现在的中等及偏难题；从过去的直接套用公式，到现在通过收集的数据、直观图形来抽象出数学模型，然后通过数学计算，分析模型，构造函数，得到最优解，这些问题无一不是数学核心素养在高考中的体现.

例2某公司为了能够进行更好的发展，需要对公司进行宣传，为了确定下一年度宣传费的投入，对近8年的宣传费xi和年销售量yi（i=1，2，3，…，8）数据作了初步处理，得到下面的散点图及一些统计量的值，模拟年销售量y（单位：t）和年利润z（单位：千元）对年宣传费x（单位：千元）的影响.

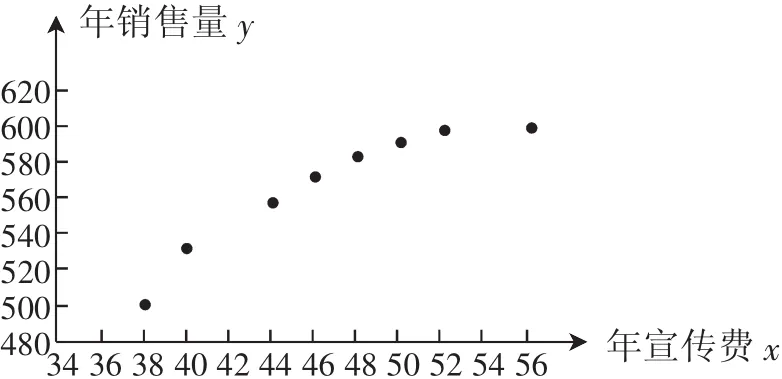
图2

∑（xi-x）2 n x y w i=1 46.6 563 6.8 289.8∑（wi-w）2 n∑（xin∑（win i=1 i=1 x）（yi-y）i=1 w）（yi-y）1.6 1469 108.8

（2）根据（1）的判断结果及表中数据，建立y关于x的回归方程；

（3）已知这种产品的年利率z与x、y的关系为z=0.2yx.根据（2）的结果回答下列问题：①年宣传费x=49时，年利润及年销售量的预报值是多少？②年宣传费x为何值时，年利润的预报值最大？

分析：根据散点图，通过直观想象，本题应该不是线性回归问题，通过排除法或者图形的特点，得到适宜作为年销售量y关于年宣传费x的回归方程.然后通过整体代换令即通过数据运算及逻辑推理把不熟悉的问题变为熟悉的问题，先建立y关于w的线性回归方程，根据公式可以计算得到：

所以y关于w的线性回归方程为yˆ=100.6+68w.

根据模型，通过数据运算、分析，然后预测结果.

由（2）知，当x=49时，年销售量y的预报值

年利润z的预报值zˆ=576.6×0.2-49=66.32.

在第三问中，①是一种特殊的情况，然后从特殊到一般得到一个无理函数，再根据逻辑推理对无理函数进行整体代换，把无理函数转化为二次函数，根据二次函数的图像和性质得到最值，从而为我们的日常生活生产服务.

根据（2）的结果知，年利润z的预报值

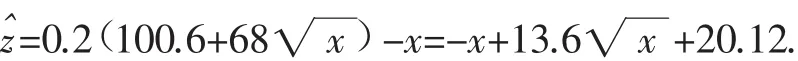
所以当，即x=46.24时取得最大值.

故年宣传费为46.24千元时，年利润的预报值最大.

如果平时在学习中只靠刷题来提高数学成绩的同学，可能大多数在高考时对于本题只能是望洋兴叹了，平时只是做过线性回归的直线方程问题，而这道题很显然换了一身新的“马甲”——非线性关系.这也从侧面反映了我们在教学过程中轻过程重结果，忽视了知识生成的思维过程，只注重机械的练习，这不符合现在新课改的要求.同时在第（2）（3）问中，使我们理解到数学不只是为了学习数学而学习数学，而是通过对数学的学习来分析世界并服务世界，这些都符合现在课改的精神.现在的大纲提出来的六大核心素养，把新的问题转化为我们所熟悉的问题，将复杂的问题简单化，都需要我们注重过程教学，培养学生的思维，注重核心素养在课堂教学中的渗透.

例3从区间［0，1］随机抽取2n个数xi，yi（i=1，2，3，…，n）构成n个数对（xi，yi）（i=1，2，3，…，n），其中两数的平方和小于1的数对共有m个，则用随机模拟的方法得到的圆周率π的近似值为______.

分析：这道题目是必修三几何概率中估算圆周率π的一个“撒黄豆”实验，但是在这道题中，命题人把黄豆改为随机数，很多学生就不知所云.

（1）由几何概率可知：记“两数的平方和小于1”为事件A，记“在区间［0，1］任取两个实数”为事件B，如图3，

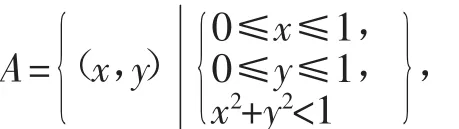
即

图3

本题是一道关于圆周率π的值的估算问题，我们实际上可以通过几何概型和随机模拟实验的方法来解决圆周率π和曲边图形的面积问题，要学会用数学的眼光来解决我们现实生活中遇到的问题，然后还可以进一步升华：我们古人是如何来估算圆周率π呢？这样既可以活跃学生的思维，也可以渗透微积分等思想，还可以在教学中加入爱国主义教育等内容，这也符合我们新课程改革的精神.

上面的这些题目学生的得分率普遍不高，从学生的角度来看：一方面，这反映了很多学生学习的方法只是习惯性听，然后做笔记，做作业时，只是习惯性的模仿，记忆一些结论和性质，在考试时，碰到熟悉的问题，就得心应手，但是碰到新的问题，就束手无策；另一方面也表现出学生在面对困难时的态度还不够积极，遇到困难容易放弃.从教师的角度来看：教师在教学过程中，只注重概念、公式等的最终结果，而忽视了学生学的过程；只重视学生对一些结论的记忆，而忽视了这些结论的推导过程；只注重教师的讲，而忽视了学生的学.

这些问题我们应该如何来解决呢？现在的“流行语”——数学六大核心素养（直观想象、逻辑推理、数学建模、数学运算和数据分析及数学抽象），它能够很好的把“不会的问题”转化为我们“会的问题”，在解决问题时，这六大素养既相互独立，又相互交汇.

如何在数学教学中渗透数学的六大核心素养呢？

然后由两种方法计算出的概率相等，从而可以估算出圆周率π的值为

（1）要让民主“走进”课堂.我们现在很多课堂还停留在教师满堂讲，学生只需要安静的在台下听，记笔记就可以了，这样的课堂注定是一种高投入，低产出的低效课堂，因为学生只是被动的接受，没有形成自己的思维，学习的主动性、分析问题和解决问题的能力也没有得到很好的提高.

我们只有让学生在课堂中“开口说话”，才能使学生积极参与到课堂教学中，进而引发他们的积极思考，只有这样，学生们的想法才能得到充分的展示，在讲解时，思维过程才能更贴近学生的实际认知水平，更能让学生接受.从另一个方面来讲不同的方法自由的发挥，让学生把各种想法都展示出来，再与学生一一分享、探讨，这样也能实现师生之间的教学相长.

（2）教学过程要符合学生的认知规律.笔者曾有幸聆听了陶维林老师的两节课，课堂对概念的讲解，让人感觉非常的自然、入理.他讲解时往往是从特殊（特殊的实例，及数据）到一般（归纳总结结论、性质）、从个别到总体，个体和特殊能够给学生直观形象，整体和一般就是引导学生通过数学直观抽象出概念和性质，然后从一般到特殊，可以让学生加深概念和性质的理解及运用，这样既做到了分析过程，又做到了知识的拓广及思维的训练，这个过程实际上就是数学的六大核心素养在教学中的综合体现，也只有这样，我们的学生才能拥有自己的思维，才能在考试中做到举一反三.

（3）不要忽视学生在学习过程中遇到的问题.只要是学习，那么就总有犯错的时候，有些教师对待学生在课堂中出现的问题，可能为了教学进度，采取不予理睬的态度，但是实际上学生出现的问题何尝不是我们教学中很好的素材，对于这些素材我们可以让学生积极的分析、讨论，既可以活跃学生的思维，也可以使课堂不再单调，还可以鼓励学生积极的参与到课堂中.

高考数学考试大纲在近几年增加了基础性、综合性、应用性、创新性以及数学文化、思想道德素质等内容，这些内容所反映出来的问题，就是以后想通过“题海战术”在高考中获得高分将越来越不现实，因为通过反复练习得到的知识，只是条件反射式的技能，解题时只能照葫芦画瓢、生搬硬套，稍有变化，就会出现各种各样的疏漏，有时甚至会束手无策.因此，我们教师在教学过程中一定要注意知识的生成性教学，把数学学科的六大核心素养贯穿于整个课堂教学，只有六大核心素养在教学中得到全面的体现，我们的学生才能在高考中以不变应万变，才会由过去的学会变成一个会学的学生.F