浅谈巧解多变量取值范围的特殊策略

☉浙江省武义第一中学 龚超群

对于各个变量，首先要仔细观察，利用题目所给的条件和形式将多个变量变为单一变量，简称消元.常用的消元法有代入消元、加减消元、三角换元等，本文便不作例举了.特殊的方法有整体代换消元、搁置无关元、确定主次变量、分离双变量、齐次式转化、巧用不等式、利用判别式等，希望能在通性通法之外有一些其他思路.

一、整体代换消元

例1（2008·江苏，11）设x，y，z为正实数，满足x-2y+3z=0，则的最小值是______.

解：由x-2y+3z=0，得

因为x，y，z是正实数，

评注：本题利用x-2y+3z=0，将整体代入所求的中，同时结合齐次式转化的思想，综合运用基本不等式，最后得到最值.

二、搁置无关元

通过观察和分析，发现有些变量在解题过程中没有直接影响，可以暂时搁置.

例2已知实数x，y，z满足x2+2y2+3z2=1，求x+2y的最大值.

解：由x2+2y2+3z2=1变形得：x2+2y2=1-3z2≤1，不妨设r2=1-3z2，0≤r≤1.

评注：本题利用变形发现变量z在解题过程中无关紧要，所以可以搁置，直接求关于x，y的双变量最值问题，当然也可以用不等式，如果把题目由x+2y变成ax+by的形式可以采用三角代换或者柯西不等式来解答.

三、确定主次变量

例3若存在实数y∈［1，2］，使得关于x的方程|x|（x2-y）=（y2+y）t有四个不相等的实数根，求实数t的取值范围.

解：将方程变形为关于x的函数，其中y为参数，不妨设

易知g（x）为偶函数，当x≥0时和是g（x）的两个零点.

因为y∈［1，2］，对g（x）求导得：

所以g（x）在上单调递减，在上单调递增.

所以g（x）在（0，+∞）上的最小值为

又因为存在y∈［1，2］，g（x）为偶函数，

所以由函数g（x）的图像可知：

当h（y）min＜t＜0，关于x的函数与直线f（x）=t有四个不同的交点，

即可知：关于x的方程|x|（x2-y）=（y2+y）t有四个不相等的实数根.

所以

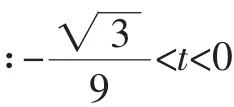
即当时，关于x的方程|x（|x2-y）=（y2+y）t有四个不相等的实数根.

评注：看似比较牵强，本题把变量y看成了一个存在性的参数，先分析并讨论了主变量x的函数变化情况，消去x之后又将y看成一个次变量，利用存在性最终得到参数t的取值范围.在分析多变量函数的恒成立问题时，经常可以采用这样的思路，分析题目中的主次变量，然后按顺序分析变量来解决问题，有时候也被称为变更主元.

如果观察到两个变量关系式可以分离为互相独立的两个函数f（x），g（y），那么分离双变量x，y，可以利用两个变量所对应的函数的值域来解决恒成立或者存在性问题.

四、齐次式转化

如果题中所给的条件是多个变量的齐次等式（或齐次不等式），可先将式子两边同时除以某个含变量的式子，然后用整体换元来减少变量；若是多个变量的齐次分式，则先将分子和分母同时除以某个变量的相同次幂，再用整体换元来减少变量.

例4若实数x，y满足xy＞0，求的最大值.

解：因为实数x，y满足xy＞0，可以将所求式子的分子分母同时除以xy，

评注：本题将分子和分母的齐次分式同时除以xy，将xy视为一个整体，达到转化为单一变量的目的，然后运用基本不等式来解答.

五、巧用不等式

很多文章都论述了运用基本不等式和柯西不等式来解决双变量问题的思想方法，不等式运用过程中最大的特点是“凑”和“巧”，很多双变量问题都可以运用不等式来解决.

例5设单位向量a，b的夹角为锐角，若对任意的实数（x，y）∈（{x，y）||xa+yb|=1，xy≥0}，都有成立，求a·b的最小值.

解：设单位向量a，b的夹角为θ，由（x，y）∈{（x，y）||xa+yb|=1，xy≥0}，

得：x2+y2+2xycosθ=1. ①

因为对任意的实数（x，y）都有成立，

由①代入“1”得：15x2+60xy+60y2≤64（x2+y2+2xycosθ）.若对任意的实数（x，y）恒成立，则60-128cosθ≤恒成立，由基本不等式得，即a·b的最小值为

评注：本题先由向量的模得到一个含有参数θ的等式，然后对恒成立问题简化出来的“64”和等式中的“1”进行灵活代换，并采用将参数θ分离的策略，最后运用基本不等式解决比较巧妙.

六、利用二次方程的判别式

以上几种方法都可以利用已知条件将多变量变为单一变量，但是有的时候根据题目所给的条件，运用消元法比较困难或者无法消元，此时可以采用二次方程的判别式进行求解.

例6（2011·浙江理，16）设x，y为实数，若4x2+y2+xy=1，求2x+y的最大值.

答：设2x+y=t，则y=t-2x，代入4x2+y2+xy=1得：

4x2+（t-2x）2+x（t-2x）=1⇒6x2-3tx+t2-1=0，

则关于x的方程必定有解，由判别式Δ≥0恒成立可解得所以2x+y的最大值为

评注：本题的解题方法比较多，也比较灵活，但是综合判断还是运用判别式的方法比较简洁.F