雨后静观“题”意思
——对一道高考题的再研究
2019-05-29山东省昌邑市教研室付世安
☉山东省昌邑市教研室 付世安
☉山东省单县第一中学 卫小国
一、试题呈现
(2017年全国Ⅰ卷理科第20题,下文简称第20题)已知椭圆,四点P(11,1),P(20,1),中恰有三点在椭圆C上.
(1)求C的方程;
(2)设直线l不经过P2点且与C相交于A,B两点.若直线P2A与直线P2B的斜率的和为-1,证明:l过定点.
第20题内涵丰富、背景深邃,文[1]进行“一题多解、一题多变”,推广得出一般性质;文[2]改“斜率之和”为“斜率之积”略作论证.笔者研读,收获颇丰,却顿生疑惑:“斜率之积为定值”与“直线过定点”等价吗?性质是否为圆锥曲线的统一性质?笔者以斜率之积不为零且取圆锥曲线的右顶点为例,深入探究,终有所获,现成文以供研讨.
二、拓展研究
“斜率之积为定值”与“直线过定点”的充要条件的探究.
1.充要论证
命题1:设椭圆为椭圆的右顶点,直线l与椭圆相交于C,D两点,且kAC、kAD分别为直线AC、AD的斜率,则直线l过定点的充要条件是kAC·kAD为定值.
证明:假设斜率之积为定值λ,易知直线l斜率为0时不符合.设与椭圆联立,化简得(b2+
另一方面,设直线过x轴定点(n,0),即l:y=k(x-n),与椭圆联立,化简得:
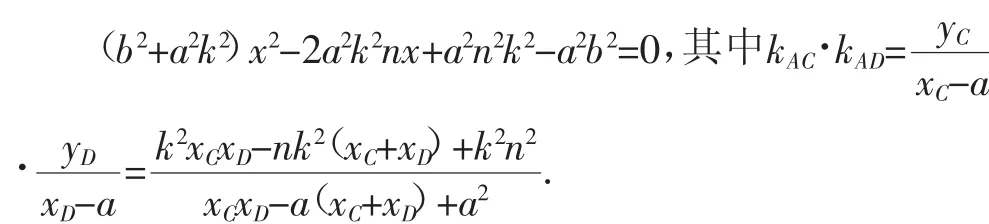
综上所述,直线l过定点的充要条件是kAC·kAD为定值.
特别指出,若直线l与x轴交点的横坐标为时,可得于是有如下结论:
定理1:设椭圆为椭圆的右顶点,直线l与椭圆相交于C,D两点,且kAC、kAD分别为直线AC、AD的斜率,则直线l过x轴上定点的充要条件是为定值λ.
2.问题变式
斜率之积为定值与直线过定点的等价,在一般椭圆中是成立的.下面猜想在双曲线、抛物线中的情形,并论证.
命题2:设双曲线为双曲线的右顶点,直线l与双曲线相交于C,D两点,且kAC、kAD分别为直线AC、AD的斜率,则直线l过x轴上定点的充要条件是为定值λ.
证明:假设斜率之积为定值λ,易知设直线l斜率为0时不符合.设与双曲线联立,化简得
另一方面,设直线过x轴定点(n,0),即l:y=k(x-n),此时类比椭圆同理可证.
于是在圆锥曲线中可以推广至双曲线,而在抛物线中的结论略有不同,更显简洁.
命题3:抛物线y2=2px(p>0),O为抛物线的顶点,直线l与抛物线相交于C,D两点,且kOC、kOD分别为直线OC、OD的斜率,则直线l过定点的充要条件是kOC·kOD为定值λ.
证明:假设斜率之积为定值λ,易知直线l斜率为0时不符合.设l:y=kx+m,与抛物线y2=2px(p>0)联立可得:k2x2+(2km-2p)x+m2=0.
另一方面,设直线过x轴定点(n,0),即l:y=k(x-n)与抛物线y2=2px(p>0)联立可得k2x2-(2k2n+2p)x+k2n2=0,
于是有如下结论:
定理2:设抛物线y2=2px(p>0),O为抛物线的顶点,直线l与抛物线相交于C,D两点,且kOC、kOD分别为直线OC、OD的斜率,则直线l过定点的充要条件是为定值λ.
三、命题应用
上述结论揭示了圆锥曲线内“斜率定积,线过定点”的优美性质,阐释了“化动为静,以静制动”的思想方法.而且借助变式,不难解答以下问题.
题1(人教B版选修2-1第73页教材习题)过抛物线的顶点O作互相垂直的弦OA和OB.
求证:弦AB与抛物线的对称轴相交于定点.
简解:设抛物线方程为y2=2px(p>0),根据kOA·kOB=-1,根据定理2,容易求得定点为(2p,0).
题2(2013年卓越联盟自主招生考试)设椭圆的离心率为,斜率为k的直线l过点E(0,1)且与椭圆交于C,D两点.
(2)设A为椭圆的下顶点,kAC、kAD分别为直线AC、AD的斜率,证明:对任意的k,恒有kAC·kAD=-2.
简解:(2)类比椭圆命题定理1,当A为椭圆的下顶点时,直线l恒过y轴定点
把a2=6,b=2,yE=1代入得,λ=-2.命题得证.
题3(2018年浙江教育评价联盟)设椭圆=1(a>b>0)的左、右焦点分别为F1,F2,焦距为2,长轴长为4.
(1)略.
(2)设过点F1的直线l与椭圆交于C,D两点,试问是否存在x轴上定点M,使得MC,MD的斜率之积为定值?若存在,求出定值与定点;若不存在,说明理由.
简解:椭圆直线CD交x轴于定点(-1,0).
当M为椭圆右顶点(2,0)时,有
此时,定点为(-2,0),MC,MD的斜率之积为
