对一道高考题的多解探究

☉浙江省玉环市玉城中学 张夏飞

我国南宋时期杰出的数学家杨辉曾说：“夫学算者，题从法取，法将题验，凡欲明一法，必设一题.”其实，在教材中所选用的例题、练习题都是经过专家们再三选取、提炼而来的，能帮助我们有效地明晰概念、掌握方法.充分感受教材中所选用的例题、练习题中丰富的内涵，从而达到举一反三的目的，并提高分析问题和解决问题的能力.

一、高考真题

（2018·全国Ⅲ卷文、理·22）在平面直角坐标系xOy中，⊙O的参数方程为θ为参数），过点（0，且倾斜角为α的直线l与⊙O交于A，B两点.

（1）求α的取值范围；

（2）求AB中点P的轨迹的参数方程.

本题以参数方程与普通方程的互化为问题背景，通过直线与圆的位置关系、中点弦问题来考查化归与转化思想、运算求解能力以及数学运算与直观想象等数学核心素养.

二、官方标答

解：（1）⊙O的直角坐标方程为x2+y2=1.

（2）方法1：l的参数方程为（t为参数

设A，B，P对应的参数分别为则，且满足

又点P的坐标（x，y）满足

所以点P的轨迹的参数方程是（α为参数

点评：第（2）小题求解AB中点P的轨迹的参数方程，借助直线l的参数方程与普通方程的转化，采用韦达定理，并结合中点坐标公式，通过三角恒等变换的转化来确定点P的轨迹的参数方程.其实，解决第（2）小题中AB中点P的轨迹的参数方程问题，切入点各异，方法众多.

三、巧思妙想

1.解几思维

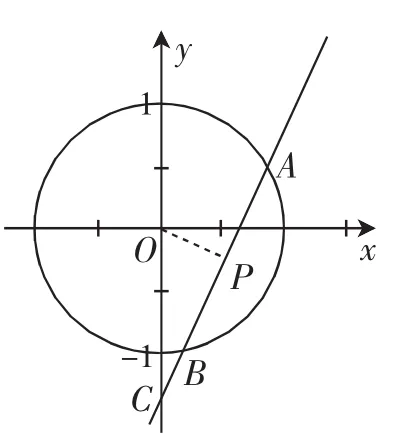
图1

（2）方法2：由题知⊙O的直角坐标方程为x2+y2=1，设点C的坐标为连接OP，由于P是AB的中点，则有OP⊥AB.

设P（x，y），当P不为O点时，设OP的直线方程为y=kx，则CP的直线方程为

而点P在⊙O内，所以AB中点P的轨迹方程是x2+y2+其对应的参数方程为β为参数，0＜β＜π）.

点评：通过平面几何中的垂径定理，利用解几法中的交轨法，结合相应的直线方程来确定对应的P（x，y）的轨迹方程，并结合两圆相交弦所在的直线方程以及图形直观来确定参数y的取值范围，进而把普通方程转化为对应的参数方程即可得以解决.

2.设而不求思维

（2）方法3：由题知⊙O的直角坐标方程为x2+y2=1.

设P（x，y），A（x1，y1），B（x2，y2），则x12+y12=1，x22+y22=1.

两式相减可得x12-x22+y12-y22=0，即（x1+x2）（x1-x2）+（y1+y2）（y1-y2）=0.又

而点P在⊙O内，所以AB中点P的轨迹方程是x2+y2+其对应的参数方程为β为参数，0＜β＜π）.

点评：通过设出相应点的坐标，利用设而不求的思维，通过中点弦中的点差法建立关系式，并结合中点坐标公式与直线的斜率公式加以转化来确定对应的点P（x，y）的轨迹方程，结合两圆相交弦所在的直线方程以及图形直观来确定参数y的取值范围，进而把普通方程转化为对应的参数方程即可得以解决.

3.函数方程思维

4（1+k2）＞0，即k2＞1，从而即，代入，可得

所以将其代入，整理可得x2+y2+

又因为k2＞1，所以＜0，即所以AB中点P的轨迹方程是

所以AB中点P的轨迹方程是其对应的参数方程为β为参数，0＜β＜π）.

其实，在日常解题过程中，应不满足于一种解法，多思则多解，这样在遇到具体问题时才能真正做到随机应变，从而达到快速求解的目的.充分运用一题多解，可以从多角度、多途径寻求解决问题的不同方法.同时，从多种解法的对比中选取最佳解法、通性通法、特殊解法等，总结解题规律，提高分析问题、解决问题的能力，真正达到思维的发散性和创新性，培养数学核心素养.F