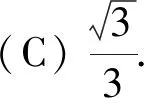利用摩擦角巧解平衡态
2019-05-29席明珍
席明珍
(白银市教育科学研究所,甘肃 白银 730900)
1 物体在μ
图1
例1.(2018年山东省师大附中高三上学期第3次模拟)倾角为θ=37°的斜面上有一重物G的物体A,A与斜面间的动摩擦因数μ=0.5.现给A施加一个水平力F,如图1所示.最大静摩擦力等于滑动摩擦力,物体A在斜面上静止,则水平力F与G的比值可能是
(A) 2. (B) 1. (C) 0.5. (D) 0.1.

(1) 如图2所示,水平外力F取最小值时,物体A将沿斜面向下刚好滑动β取得最小值,有βmin=θ-α,对等式两边取正切得
(2) 如图3所示,水平外力F取最大值时,物体A将沿斜面向上刚好滑动β取得最大值,有βmax=θ+α,对等式两边取正切得

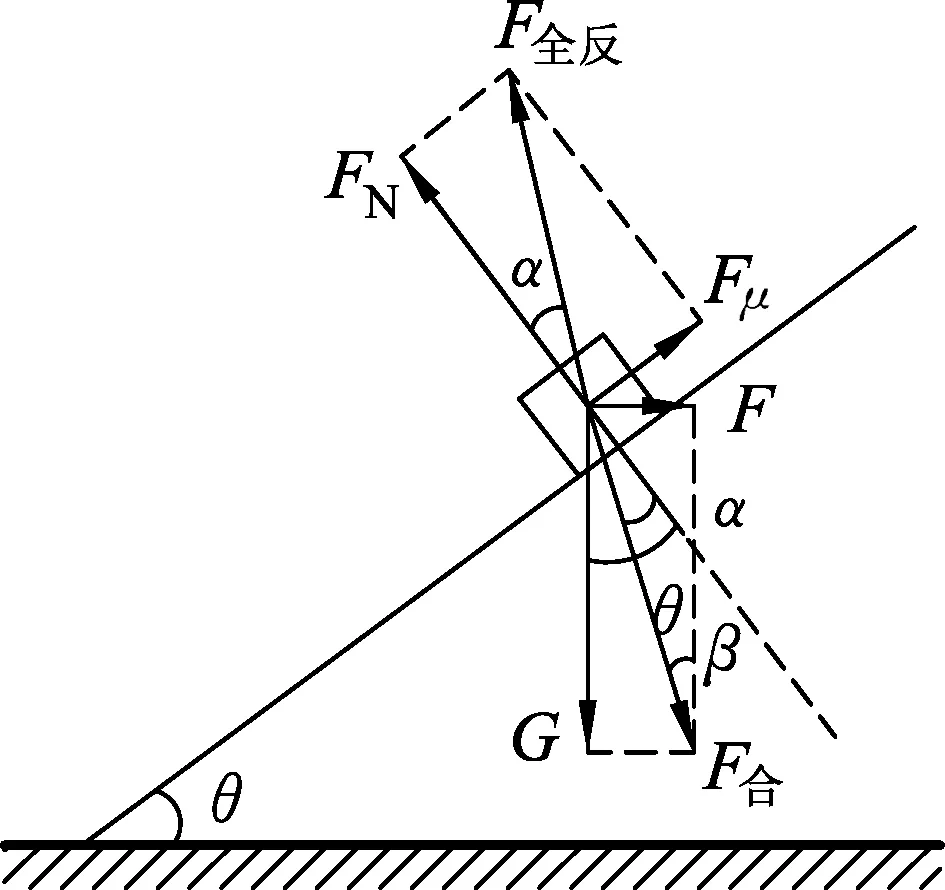
图2

图3
析评:因为物体处于静止状态,斜面施加给物体的支持力和静摩擦力的合力与外力和重力的合力是一对平衡力,随外力增大,这一对合力将逆时针旋转,合力垂直斜面方向时静摩擦力为0.静摩擦力取得最大时,静摩擦力将变为滑动摩擦力,合力与垂直斜面方向的夹角为摩擦角.合力与竖直方向的夹角最小为斜面倾角和摩擦角之差,最大为斜面倾角和摩擦角之和,由这一夹角的范围直接确定了外力的范围,这是应用摩擦角的闪光之处.
2 受斜面向上方向恒定外力约束的物体将要沿斜面向下滑动时,斜面倾角等于摩擦角的2倍
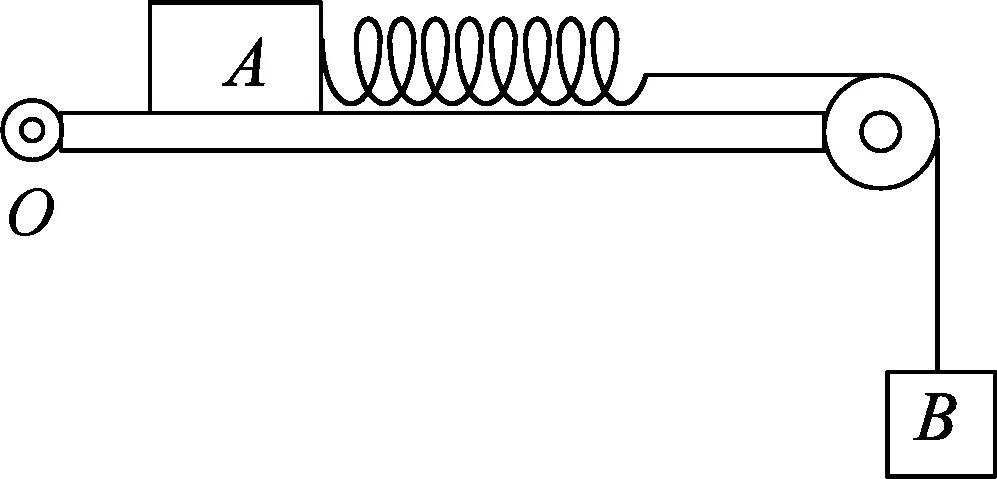
图4
例2.如图4所示,粗糙木板的一端固定在转轴上,另一端固定有定滑轮,物块A置于木板上,通过轻弹簧与细绳跨过定滑轮与物块B相连.物块A的质量为M,物块B的质量为m,且M=2m,已知物块A与木板间的动摩擦因数μ=0.5,且最大静摩擦力与滑动摩擦力相等,最初木板水平,在木板绕轴逆时针缓慢转动到物块A恰好不下滑的过程中,下列说法正确的是
(A) 弹簧长度逐渐增大.
(B) 物块A与木板间的摩擦力逐渐增大.
(C) 物块A对木板的压力先减小后增大.
(D) 当物块A恰好不下滑时,木板与水平面间的夹角为53°.
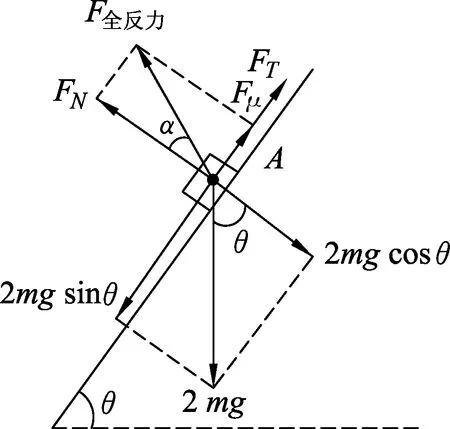
图5

图6
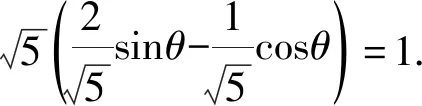
3 斜面倾角大于摩擦角时,物体沿斜面加速下滑
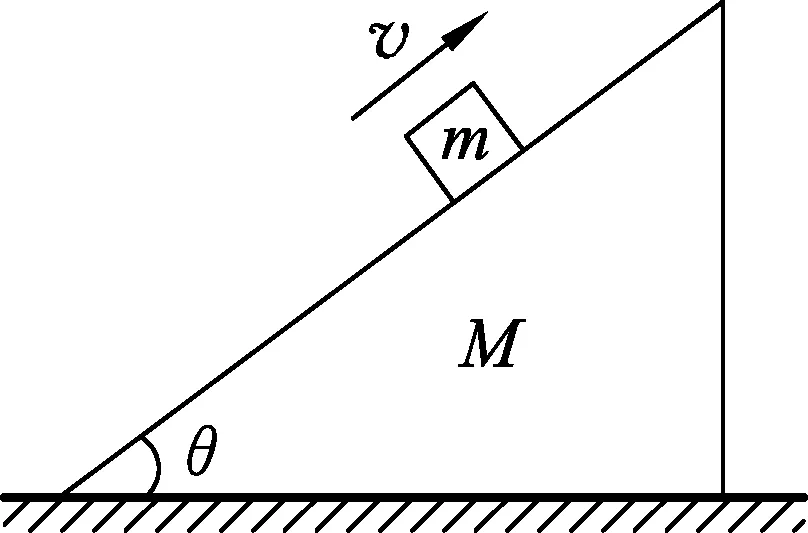
图7
例3.如图7所示,质量为M的斜劈形物体放在水平地面上,质量为m的粗糙物块以某一初速度沿斜劈的粗糙斜面向上滑,至速度为0后又加速返回,而斜劈M始终保持静止,则
(A) 地面对斜劈M的摩擦力大小相同.
(B) 地面对斜劈M的支持力总小于(M+m)g.
(C) 地面对斜劈M的摩擦力先向右后向左.
(D) 地面对斜劈M的摩擦力先向左后向右.


图8

图9
析评:动摩擦因数μ4 在两次大小相同、方向不同的外力作用下物体沿水平面均做匀速直线运动,则这两次大小相同的外力关于最小外力对称
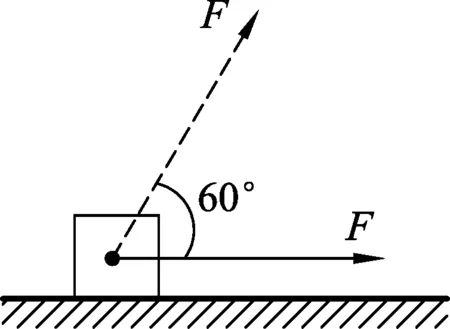
图10
例4.(2017年全国卷Ⅱ)如图10所示,物块在水平拉力F的作用下沿水平桌面做匀速直线运动.若保持F的的大小不变,而方向与水平面成60°角,物块也恰好做匀速直线运动.物块与桌面的动摩擦因数为

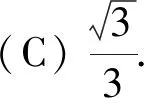


图11
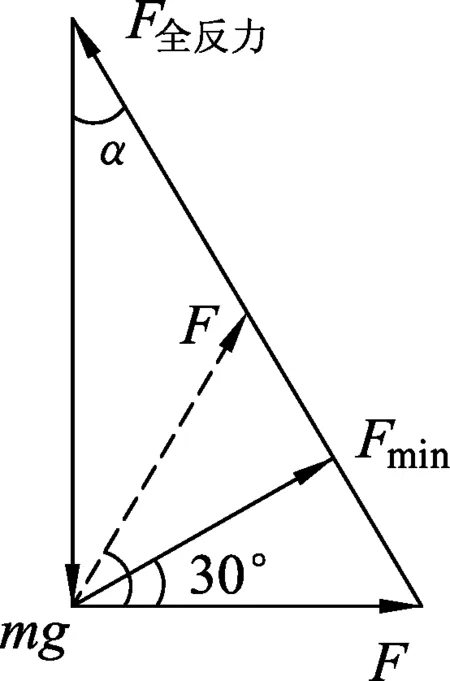
图12
析评:在顶角为摩擦角的力的矢量三角形中,由两次外力的对称性和夹角,在三角形的边角关系中,直接读出摩擦角α的大小,操作显而易见,是快速求出动摩擦因数μ的首选方法.

图1
例1.(2018年山东省师大附中高三上学期第3次模拟)倾角为θ=37°的斜面上有一重物G的物体A,A与斜面间的动摩擦因数μ=0.5.现给A施加一个水平力F,如图1所示.最大静摩擦力等于滑动摩擦力,物体A在斜面上静止,则水平力F与G的比值可能是
(A) 2. (B) 1. (C) 0.5. (D) 0.1.

(1) 如图2所示,水平外力F取最小值时,物体A将沿斜面向下刚好滑动β取得最小值,有βmin=θ-α,对等式两边取正切得
(2) 如图3所示,水平外力F取最大值时,物体A将沿斜面向上刚好滑动β取得最大值,有βmax=θ+α,对等式两边取正切得


图2

图3
析评:因为物体处于静止状态,斜面施加给物体的支持力和静摩擦力的合力与外力和重力的合力是一对平衡力,随外力增大,这一对合力将逆时针旋转,合力垂直斜面方向时静摩擦力为0.静摩擦力取得最大时,静摩擦力将变为滑动摩擦力,合力与垂直斜面方向的夹角为摩擦角.合力与竖直方向的夹角最小为斜面倾角和摩擦角之差,最大为斜面倾角和摩擦角之和,由这一夹角的范围直接确定了外力的范围,这是应用摩擦角的闪光之处.
2 受斜面向上方向恒定外力约束的物体将要沿斜面向下滑动时,斜面倾角等于摩擦角的2倍

图4
例2.如图4所示,粗糙木板的一端固定在转轴上,另一端固定有定滑轮,物块A置于木板上,通过轻弹簧与细绳跨过定滑轮与物块B相连.物块A的质量为M,物块B的质量为m,且M=2m,已知物块A与木板间的动摩擦因数μ=0.5,且最大静摩擦力与滑动摩擦力相等,最初木板水平,在木板绕轴逆时针缓慢转动到物块A恰好不下滑的过程中,下列说法正确的是
(A) 弹簧长度逐渐增大.
(B) 物块A与木板间的摩擦力逐渐增大.
(C) 物块A对木板的压力先减小后增大.
(D) 当物块A恰好不下滑时,木板与水平面间的夹角为53°.

图5

图6
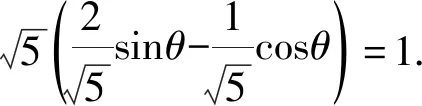
3 斜面倾角大于摩擦角时,物体沿斜面加速下滑

图7
例3.如图7所示,质量为M的斜劈形物体放在水平地面上,质量为m的粗糙物块以某一初速度沿斜劈的粗糙斜面向上滑,至速度为0后又加速返回,而斜劈M始终保持静止,则
(A) 地面对斜劈M的摩擦力大小相同.
(B) 地面对斜劈M的支持力总小于(M+m)g.
(C) 地面对斜劈M的摩擦力先向右后向左.
(D) 地面对斜劈M的摩擦力先向左后向右.


图8

图9
析评:动摩擦因数μ 图10 例4.(2017年全国卷Ⅱ)如图10所示,物块在水平拉力F的作用下沿水平桌面做匀速直线运动.若保持F的的大小不变,而方向与水平面成60°角,物块也恰好做匀速直线运动.物块与桌面的动摩擦因数为 图11 图12 析评:在顶角为摩擦角的力的矢量三角形中,由两次外力的对称性和夹角,在三角形的边角关系中,直接读出摩擦角α的大小,操作显而易见,是快速求出动摩擦因数μ的首选方法.4 在两次大小相同、方向不同的外力作用下物体沿水平面均做匀速直线运动,则这两次大小相同的外力关于最小外力对称