对一道力学竞赛题解析的商榷

朱 挺

(江苏省启东中学,江苏 启东 226200)

中国科技大学出版社出版的《加拿大物理奥林匹克》一书中,有这样一道题:多伦多物理奥林匹克竞赛团队为去年在POPTOR周末表现优秀的学生铺设了一张红地毯．比赛结束后他们决定把地毯卷起来放在储藏室．在卷地毯的过程中,他们注意到了一个完美的物理问题．

假设有一条很长的地毯,厚度t非常小,已知其宽度W、长度L和密度ρ,有一部分已经卷成半径为r的圆柱体．由于厚度很小,已经卷起的地毯可以看作完美的圆柱体．我们希望只通过踢一下圆柱部分的地毯,使它获得大小为v的初始速度,就可以把整个地毯卷起来如图1所示．求所需要的最小初始速度v．

图1

书中给出如下解析.地毯的动能为

(1)

其中M1=πr2Wρ是已经卷起来部分的地毯的质量．而全部地毯的质量为M,在卷地毯的过程中地毯势能增加,其重心将不断地升高．当地毯全部卷起后,半径将变为

重心升高了 Δh=rf-r.

势能改变量为

ΔEp=Uf-Ui=Mgrf-M1gr=

(2)

动能全部转化为地毯重心上升而增加的势能,联立两式可求得速度

(3)

对于上述解析,笔者认为存在不完善的地方．若原题解析认为已卷起部分,在踢一下之后立即作纯滚动,则原解析思路是正确的．但是在计算初动能时缺少了转动动能．

正确解析是这样的:由纯滚动条件,v=ωr,故初动能

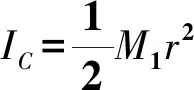
由机械能守恒得

若已卷起部分地毯做初速度v的平动,必然经历一个连滚带滑的过程.这个过程由于摩擦力做功,因而机械能不守恒，故原解析存在一个原则性的错误．

具体分析如下:通过踢一下圆柱体,给它一个平动的初速度,使该圆柱体滑动,同时,地面对圆柱体的摩擦力使平动减速,同时对圆柱体中心轴的力矩,使圆柱体具有顺时针方向角加速度．角速度从0开始增加,经过一段时间,转化为纯滚动．而在这个过程中,圆柱体将会损失部分的机械能,故整个过程机械能是不守恒的．原题的解析忽视了连滚带滑这一环节．

正确的解答如下:

全过程分成两个阶段.

第一阶段,圆柱体由连滚带滑转化为纯滚动的过程中,圆柱体和地平面相切的切线pp′为轴,角动量守恒．

M1vr=ICω+M1v1r.

ωr=v1式中ω是圆柱体做滚动时绕中心轴转动的角速度,v1是圆柱体做纯滚动时中心的平动速度.可得

第二阶段,纯滚动过程,满足机械能守恒:

势能的变化量同原题.

由Ek=ΔEp可得

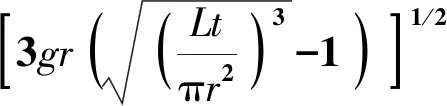
综上所述,原题对初始状态描述不清晰,原解析没有对地毯的运动过程进行充分地讨论,最终导致了原解析的不完善．