SF6分子最高占据轨道对称性的判断*

武瑞琪 郭迎春† 王兵兵

1) (华东师范大学物理与材料科学学院,上海 200241)

2) (中国科学院物理研究所,凝聚态物理国家研究中心,光物理实验室,北京 100190)

量化计算是理论研究分子的重要手段,对于具有高对称群的分子,采用子群计算是常用的方法.分子的电子态或分子轨道等的对称性在子群的表示中会出现重迭,从而不能从子群的结果直接给出电子态或分子轨道对称性的归属.本文以如何判断SF6基态 1 A1g 的电子组态中最高占据轨道的对称性为例来解决这个问题.针对某些文献中的SF6基态 1 A1g 的电子组态中,最高占据轨道对称性是T1g却写成T2g的问题,采用Molpro量化计算软件,对SF6基态的平衡结构,进行了HF/6-311G*计算,得到了能量三重简并的最高占据轨道的函数表达式,进而运用Oh群的对称操作作用在三个轨道函数上,得到各操作的矩阵表示,于是得到特征标,最后确定了最高占据轨道为T1g 对称性.

1 引言

多原子分子的电子结构及能级的准确计算是研究复杂分子的电离、解离和光辐射等动力学过程的基础.准确掌握复杂分子的能级结构和电子空间分布已经成为物理化学领域的重要研究方向.量化计算是理论研究分子的重要手段,电子组态的确定是确定分子结构的重要一环,电子组态离不开电子轨道对称性的准确描述.对于具有高对称群的分子,采用子群计算是常用的方法.然而分子的电子态或分子轨道等的对称性在子群的表示中会出现重迭,因此不能从子群的结果直接给出电子态或分子轨道对称性的归属.如何由子群的结果获得分子轨道对称性的归属是本文关心的问题,本文将以探讨属于 Oh群的SF6分子的最高占据轨道的对称性为例来说明.

SF6是一种惰性气体分子,是很好的绝缘介质,常被用于断路器、开关设备及传输线等材料中[1-3].因为SF6分子对低能电子具有较大的吸收截面[4,5],它被广泛应用于电子捕获材料.在高分子领域,SF6更是重要的聚合物掺杂剂,由于SF6可以从高分子聚合物中吸收一个电子而在聚合物链上形成空穴,所以带有SF6掺杂的聚合物呈现明显的导电性.此外,S F6也是一种重要的温室气体,温室效应远大于 C O2[6],所以SF6的排放链被严格控制,其形成和解离过程也成为研究热点.

近年来,对于SF6分子电子结构、电子组态及以S-F原子距离为函数的势能曲线等已开展了大量的研究工作.文献[7—11]给出了SF6基电子态1A1g的电子组态为(core)22(4a1g)2(3t1u)6(2eg)4(5a1g)2(4t1u)6(1t2g)6(3eg)4(1t2u)6(5t1u)6(1t1g)6,最高占据轨道的对称性为T1g; 实验上文献[12—15]给出了关于电子动量谱学 T1g等轨道的信息.文献[5,16,17]则认为最高占据轨道的对称性为 T2g.产生这种分歧的原因在于：对SF6的量化计算中采用的是Oh群的对称阿贝尔子群D2h群,从而波函数的对称性由D2h群的对称性进行描述,S F6最高占据的三条简并轨道的对称性分别表达为D2h中的B1g,B2g和B3g,而 Oh中的不可约表示与D2h中的不可约表示不是一一对应的,Oh中的不可约表示T1g和T2g在D2h中都约化成B1g,B2g和B3g的和,所以不能从量化计算的结果直接区分开T1g和T2g.轨道对称性的正确认识会影响选择定则的确定,更会决定光谱的正确指认.本文通过具体分析最高占据轨道的波函数,结合群论的理论,验证了SF6基态的最高占据轨道的对称性为T1g而不是T2g,通过SF6这个例子,本文为高对称分子的轨道对称性的判断提供了方法.本文的安排如下,第2 节采用HF/6-311G*给出最高占据轨道的波函数,第3节通过Oh群的对称操作作用在波函数上,给出最高占据轨道对称性,最后给出结论.

2 SF6最高占据轨道的计算

SF6分子具有 Oh群对称性,所以分子中轨道的对称性用 Oh群的不可约表示来描述.Oh群具有A1g,A2g,Eg,T1g,T2g,A1u,A2u,Eu,T1u和T2u10种不可约表示,S F6的轨道函数对称性属于哪个不可约表示,则它就是该不可约表示的基函数[18].所以本文将首先给出SF6的最高占据轨道波函数,然后再确定它是哪个不可约表示的基函数.本文全篇采用原子单位.

采用Molpro软件[19],运用HF方法[20],利用6-311G*基组[21],对SF6的基电子态1A1g态进行计算,得到的电子组态中分子轨道的排序与引言中的排序相同,因此得到的电子组态是正确的.计算得到的平衡位置的核间距为2.923 a.u.,与实验值2.957 a.u.基本相符.所以计算的结果是可靠的.计算得到3条最高占据轨道能量简并,对称性分别属于D2h群的B1g,B2g和B3g,对应的波函数用ΨB1g,ΨB2g和ΨB3g表示.具体如下：

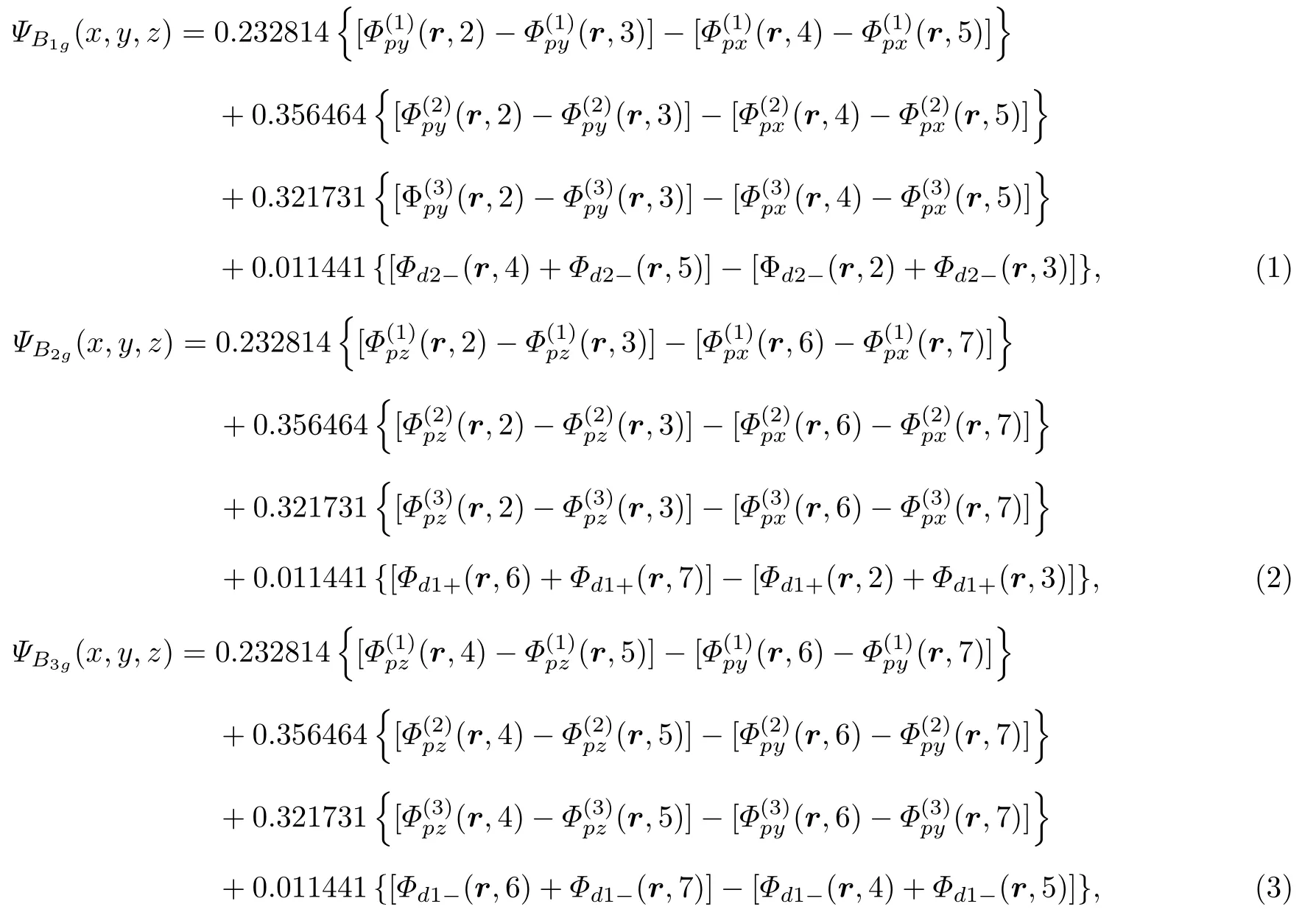
这里 w 代表电子坐标 r 的任一分量 x,y 或 z ; k=1—7对应1个S原子及6个F原子; xk,yk,zk为1个S原子以及6 个F原子的核坐标,取值如表1所列; rk是电子到第k个原子核的距离; ci表示组成原子轨道的高斯函数的系数,αi是高斯函数参数,ci与αi取值如表2所列.

为更好地理解上面的三个轨道函数以及方便后面的分析,图1给出了函数 ΨB1g,ΨB2g和ΨB3g的空间分布,颜色代表函数的取值.ΨB1g在xy截面内为中心对称的八个花瓣形状的分布(图1(c)),有四条节线,另两个截面没有节线(图1(a),(b)).ΨB2g和 ΨB3g相似,分别对应 xz 截面 (图1(d))和 yz 截面(图1(e))内的八个花瓣形状分布,在另外的两个截面内没有节线.

表1 SF6的分子结构Table 1. Molecular structure of SF6.

表2 6-311G*基组中高斯函数的参数表Table 2. Parameters of Gaussian functions of 6-311G* basis.

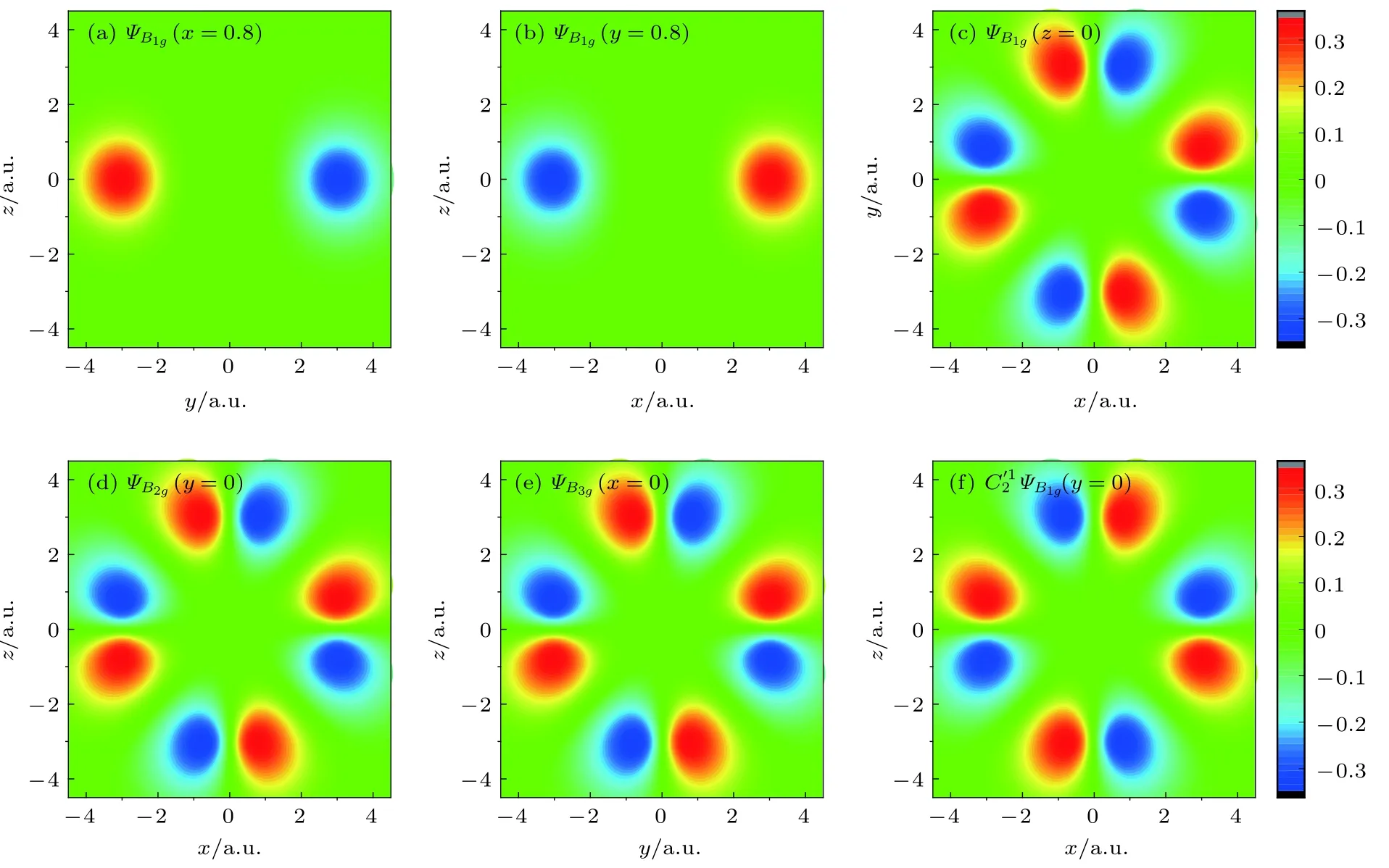
图1 ΨB1g,ΨB2g 和 ΨB3g 波函数截面图 (a) ΨB1g 在 x=0.8 a.u.处的 yz截面图; (b) ΨB1g在 y=0.8 a.u.处的 xz截面图;(c) ΨB1g 在 z=0 a.u.处的 xy 截面图；(d) ΨB2g 在 y=0 a.u.处的 xz截面图; (e) ΨB3g在 x=0 a.u.处的 yz截面图; (f) 作用在ΨB1g后取y=0 a.u.处的xz截面图Fig.1.Functions of ΨB1g,ΨB2gand ΨB3g ： (a) ΨB1g in the yz plane for x=0.8 a.u.; (b) ΨB1g in the xz plane for y=0.8 a.u.;(c) ΨB1g in the xy plane for z=0 a.u.; (d) ΨB2g in the xz plane for y=0 a.u.; (e) ΨB3g in the yz plane for x=0 a.u.; (f) the function obtained by acting on ΨB1g in the xz plane for y=0 a.u..

3 SF6最高占据轨道对称性的确定

确定SF6的三条最高占据轨道的对称性需要以下步骤： 1)以这三个函数为基函数,将 Oh的各个操作(见表3)用矩阵表示出来; 2)计算各个矩阵的迹,对比特征标表(表3给出了T1g和T2g的特征标),确定最高占据轨道的对称性.下面以操作为例具体说明.

根据计算中坐标轴的选取,如图2所示,S原子核处在正方体的重心,6个F原子核处在六个面心上,与表1中7个核的核坐标是一致的.6个的二重对称轴为图2中正方体平行且不相邻的两条棱中点的连线,共6条,采用6) 来表示6个操作.图2给出了其中的一个的对称轴,同时还给出了一个 C3轴、一个 C4轴和一个C2轴(C4轴和C2轴重合).

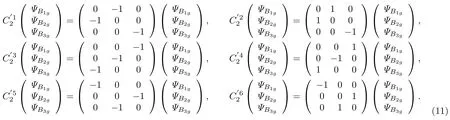
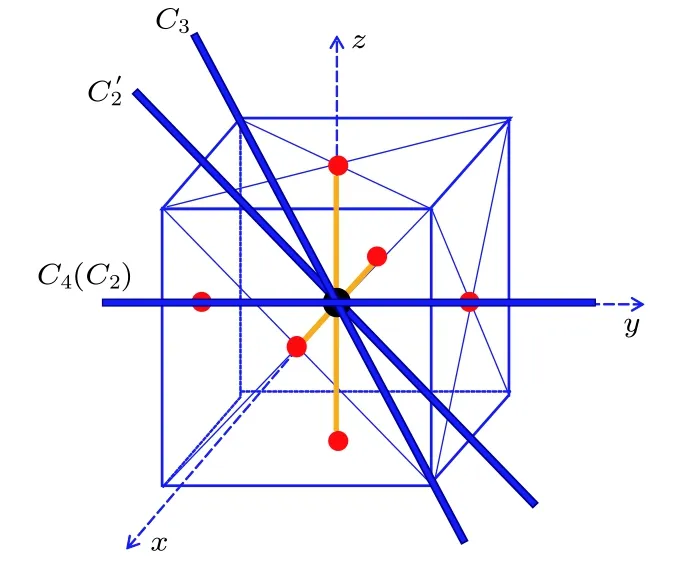
图2 SF6对称操作,C3,C4和C2的对称轴Fig.2.Symmetric axes of symmetric operators ,C3,C4and C2on SF6.

表3 Oh 群的部分特征标表Table 3. Part of character table of Oh group.

4 结 论

本文采用Molpro软件、HF方法和6-311G*基组,基于D2h对称群,计算了SF6基态1A1g态平衡结构处的波函数,得到了能量三重简并的最高占据轨道,写出了轨道的函数表达.本文进一步运用Oh群的对称操作作用在三条轨道上,确定了最高占据轨道是Oh对称群的T1g不可约表示的基函数,从而验证了SF6的基态1A1g态的最高占据轨道的对称性为T1g.本文的工作为如何判断高对称分子的分子轨道对称性的归属提供了可借鉴的方法.