以理驭法，理法融合——以《蚂蚁做操》的教学为例

浙江省义乌市香山小学教育集团 陶国强

计算教学是数学教学的重要组成部分，也是小学生学习数学知识的基础。在计算教学中如何处理算法、算理和算律的关系值得我们思考与研究。北师大的数学教材中，我们发现在计算教学编排中有主讲算理的课，如三上乘法《需要多少钱》；理法融合的课，如三下乘法单元的《队列表演（二）》；主讲算法的课，如四上乘法单元的《卫星运行时间》。另外，在有些计算教学单元学习的安排上也存在这种现象。

《蚂蚁做操》就是一节典型的理法融合的课。在本课的学习之前，学生已较熟练地学会了表内乘法，并掌握了整十、整百数及两位数乘一位数的口算方法。并且两位数乘一位数的算理在本册教材第四单元中的《需要多少钱》这一课中已经学习了。本节课是在学生学习了两、三位数乘一位数的笔算乘法的基础上，以算理驾驭算法，达到算理算法相互融合的一节课，也是今后学生进一步学习乘、除法的基础。下面就以这节课为例，谈谈如何开展理法融合的计算课教学。

一、适时呈现，解释疑惑

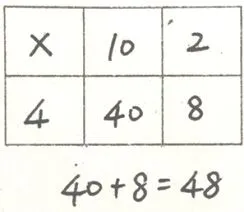
教材中经常借助点子图和列表来帮助学生理解计算的算理和意义。但是如果面对计算马上就提示使用直观模型不一定会达到良好的学习效果。有时“给”得早不如给得“巧”。如《蚂蚁做操》课中提出数学问题，列出算式12×4=之后，让学生回顾口算方法。 学生开始用了横式计算：10×4=40，2×4=8，40+8=48，教师引导：还有其他的方法吗？ 然后再汇报。

生1：我用的是列表法，把12 分成10 和2，把10 和2 分别写在表格中，乘号也写上，4×10=40，40 就 写 在10 下 面，2×4=8，8写在2 下面这一行中，最后40+8=48。

生2：我是用画点子图的方法，把点子图上下分成相同的两部分，上面部分有2 行，每行12 个，就是12×2=24，下面的也一样，24+24=48。

生3：我也是用画点子图的方法，我是把点子图分成左右两部分，左边部分是每行10个，有4 行，10×4=40；右边部分每行2 个，有这样的4 行，2×4=8；再把两部分加起来，40+8=48。

师：观察这两种方法，你更喜欢哪种？

生∶第二种看上去更容易理解，我更喜欢这种。

……

从上面环节可以看出，有时先让学生面对一个算式，不急着提供支撑算理理解的点子图或表格，让学生联系自己以前的数学学习经验来尝试解决问题，然后再适时呈现或点拨，这时学生意识到重要性后主动借助图表学到的和教师现成提供的效果是有区别的。

二、沟通联系，建立联结

数学知识本身相互之间存在着一定的联系，相同的知识呈现的形式也各有不同。数学学习就是让学生把不同形式的相同的知识给“联结”起来，建立健全知识体系。《蚂蚁做操》是学生第一次接触乘法竖式计算，运用竖式的计算过程对学生来说是比较抽象的，尤其是不容易理解竖式中每一步计算的实际含义。通过板书（线段的连接），将点子图、列表和竖式计算中的每一步相互对应起来，沟通列表数据、直观点子图、抽象竖式三者之间的内在联系，清晰地呈现出两位数乘一位数的乘法竖式的计算过程，建立有效联结。

（课件出示小组合作任务及要求）让学生说一说竖式计算每一步的意思。 合作要求：先自己独立思考，可以在作业纸上画一画，写一写。然后组长再组织组员进行交流，并选派一名组员汇报。

全班交流，展示成果。

生1：我们小组是结合圈点子图的过程来说竖式每一步意思的。点子图的每行2 个，共4 行的这一部分（2×4=8）就是竖式中第一步2×4=8，点子图中每行10 个，共4 行的这一部分（10×4=40）就是竖式中第二步10×4=40，最后再计算40+8=48。

生2：我们小组是结合列表法理解竖式每一步意思的。列表法中的2×4=8 就是竖式中第一步2×4=8，列表法中的10×4=40 就是竖式第二步10×4=40，最后把40+8=48。

生3：我们是结合横式来理解竖式每一步的意思的。竖式的第一步2×4=8 就是横式中的2×4=8，第二步10×4=40 就是横式中的10×4=40，竖式把40 和8 相加就是横式中的40+8=48。

学生点评，教师小结。

师：你们的回答都很棒，我们再来回忆一下他们的发言，竖式中的2×4=8 这一步，就是点子图中的每行2 个，共4 行的这一部分（2×4=8），就是列表法中第二行右边的2×4=8，也是横式计算中的2×4=8，计算结果都是8，我们就把8 写在个位上。

竖式中再算10×4=40 这一步，就是点子图中每行10 个，共4行的这部分（10×4=40），就是列表法中第二行左边的10×4=40，也是横式中10×4=40，计算结果是40，写在第二层，我们就把4 写在十位上，0 写在个位上。

竖式最后算的40+8=48 这步，在点子图中就是两部分之和，就是列表法中40+8=48，也是横式中的40+8=48。（教师边板书，边连线，边讲解）

师：我们会发现原来以前学习的几种方法和今天学习的竖式方法道理都是一样的，只不过形式发生了变化，从以前的“横”变成“竖”。

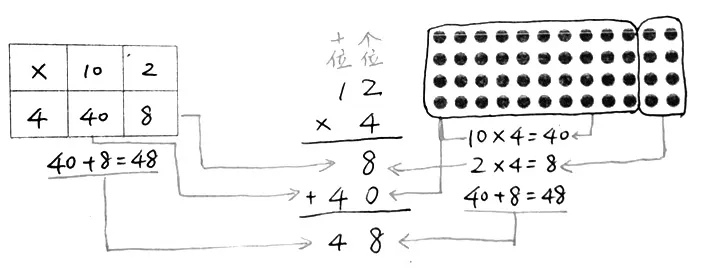
把横式、列表、点子图和竖式之间有机联系起来，让学生理解它们之间的关系，这样的联系触及了竖式计算知识各部分之间的联系，使学生对竖式计算的认识与算理思维融会贯通，对学生学习竖式计算有很大的帮助。

三、变化对比，凸显结构

在数学教学和学习中，变化对比是一种常用的方法，在对比中能让学生深刻理解和掌握相关知识，对于让学生建立正确的知识体系有重要的意义。本课教学中，让学生通过观察不同，进行对比，加深了对竖式计算的理解和明确了写法，促进了学生建构清晰的知识体系。

师：以前的这些算法和竖式计算有什么不同？（出示思考问题）

生1：以前的方法是先算10×4=40，再算2×4=8，最后算40+8=48；竖式计算是先算2×4=8，再算10×4=40，最后算40+8=48。

师：你观察得真仔细。

生2：我发现竖式计算比横式计算更简单，它用竖式把三个计算步骤都结合起来。

师：竖式是计算乘法的一种方法。不过我们用乘法竖式进行计算通常不是像我们刚才那样写的，而是这样写的（教师板书）。你能看懂吗？

生1：爸爸以前教我的时候就是这样写的。

生2：这样写就是把10 乘4 等于40 直接和8 相加了，最后等于48。

师：这种写法就是把原来的加法这一步省略掉了，直接计算写出了相加后的答案，这个算式看上去更加紧凑。

理法融合，抓住了“法”与“理”之间的联系，用直观的“理”来表达计算的“法”，有利于学生理解每一步的具体含义，有效促进对算理的理解。经历把直观形象到抽象思考的有效融合过程。在计算教学中做到在学习算法中渗透算理的教学，以理驭法，理法融合是一种行之有效的方法。