以学为中心，让学生真正成为课堂的主人

2019-05-28浙江省丽水市缙云县实验中学吴雪丽

数学大世界 2019年7期

浙江省丽水市缙云县实验中学吴雪丽

如何让学生成为课堂的主人？学生的学习积极性直接影响自己掌握数学知识，因此，教师应该构建一个和谐的课堂氛围，在课堂上给学生提供一些既与知识点有关学生也对此有兴趣的素材，让学生能够主动参加到课堂中，自觉接受知识，做到以学为中心进行数学知识的学习。

一、结合生活实践培养学生的数学化思想

和很多学科一样，数学也是从生活中不断的总结和发现出来的一门学问。在初中数学的教学过程中可以多多应用身边的具体实例、生活经历，让学生感同身受地学习数学知识，从而将数学知识联系到我们实际的生活应用中去。例如，在学习《一元一次方程》时，就是把我们生活中的实际问题与数学方程结合起来，参照教材举例如下：

问题：A 校初中二年级338 名师生乘车郊游，已有两辆车可乘坐74 人，还需租借44 个座位的校车几辆？

回忆小学课本里已经学过了列方程的解法，我们来回顾一下：

设租借需用客车x 辆，可供乘坐44x 人，再加上校车上的74 人，就是一共的338 人，最后可得：44x+74=338。

通过解这个方程，就可以算出最后的结果。在教学中多多结合生活中的数学问题，会使学生更容易进入以学为中心的学习氛围中。

二、学生在数学课堂中学会积极思考与表达

培养学生在数学课堂中学会积极思考与表达，让学生真正参与课堂的活动中来，真正成为课堂的主人，对学生的学习起到很大的促进作用。

例如：在完成直角三角形的判定定理的学习后，遇到一道练习题：在△ABC 中，∠ABC=2 ∠A，AB=2BC。求证：是直角三角形。

师问：到目前为止判定一个三角形是直角三角形的方法有几种？哪几种？

学生：到目前为止，判定一个三角形是直角三角形的方法有两种，一种是有一个角是直角的三角形是直角三角形；第二种两个角互余的三角形是直角三角形。

师问：那这个题目中有具体已知的角的度数吗？

学生：没有。

师问：那可以从哪个条件去构造？

学生：书上有学过一边上的中线等于该边的一半，这个三角形是直角三角形，结合题中有条件AB=2BC，添AB 边上的中线试试。

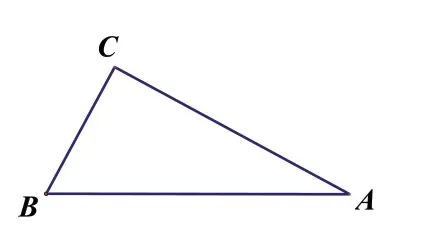
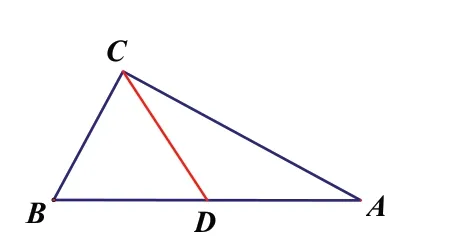
师：那我们添上BA 边上的中线CD 试试，如图。那怎么说明△ABC 是直角三角形？

生：因为CD 是BA 边上的中线，所以AB=2BD。又因为AB=2BC，所以BD=BC=CD。所以△DBC 是等边三角形。所以∠B=60°。又因为∠ABC=2 ∠A，所以∠A=30°。所以∠BCA=90°，所以△ABC 是直角三角形。

师问：为什么CD 也会等于BD？依据的是什么？

生答不上来，有学生说这个思路不行了。

师问：那谁还有其他的方法？

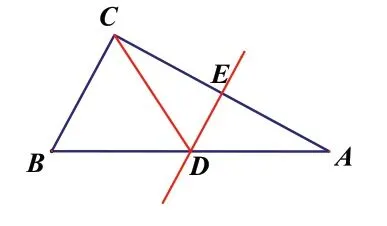
有学生说添AC 边上的垂直平分线DE，那么AD=CD 了，∠ACD=∠CAB，所以∠CDB=2 ∠A。又因为∠ABC=2 ∠A，所以∠CDB=∠CBD，所以BC=DC。所以BC=DC=DA。又因为AB=2BC，所以AB=2AD。就得到点D 是AB 的中点，所以AB 边上的中线CD 就等于AB 的一半，接下来与书上的例题证明方法一样就可以得到△ABC 是直角三角形了。

学生热烈地为他鼓掌。

还有学生叫起来：老师老师，还有方法，还有方法！

师：好，那你来说说思路。

生：题中有条件∠ABC=2 ∠A，在边AB 上取一点D 使∠DCA=∠A，就有∠CDB=2 ∠A，后面一样了。学生也热烈地为他鼓掌。

师：同学们的表现非常好，思维很不错，能从不同角度去取解决问题。那同学们还有不同的方法吗?

生：老师还有。

师：那请你来说说看。

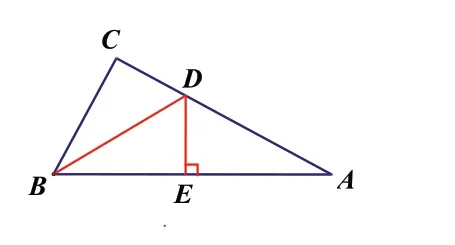
生：题中有条件∠ABC=2 ∠A，我作∠ABC 的平分线交AC于点D，就有∠DBA=∠A，所以BD=AD。再过点D 作DE 垂直于AB 于点E。所以点E 为AB 的中点，AB=2BE=2AE。又因为AB=2BC，所以BC=BE=EA。再根据SAS 证明△DBC ≌△DBE，所以∠C=∠DEB=90°。学生再次响起热烈的掌声，为他们精彩的思路而喝彩。