新课标下提高数学课堂效率初探

山东省滨州市沾化区第一中学 苏新春

新课标指出：“学生数学学习活动不应该只限于接受、记忆、模仿和练习，高中数学还应当倡导主动探索、动手实践、合作交流、阅读自学等学习方式”。这些学习方式有助于发挥学生学习的主动性，使学生学习过程成为教师引导下的“再创造”过程。所以要求我们放弃“填鸭式”的教学，构建能体现学生的主人翁地位的高效课堂是现代教育发展的必然要求。那么在新课标下如何打造高效的数学课堂就成为老师们面临的挑战。

一、在课堂上，师生营造平等和谐的气氛

首先，要尊重学生，师生平等。课堂上一定不要出现“你怎么回事？这么简单都不会，真笨”这样的话，要换用鼓励与肯定的语言“我相信你们的做法会比我的更好”。要把自己和学生置于同一地位上，“我们大家一起来讨论下这个问题”，这样学生才会以平和的心态去对待老师和课堂。

其次，老师要多鼓励学生，让每位学生都感受到肯定。课堂上多给他们微笑，挖掘每一位学生身上的闪光点，鼓励学生，不要轻易否定，这样才可以让学生充分体会老师的肯定，发现他们自身的优点。

最后，老师要充当学生互动的组织者和参与者。老师的参与，可以发现自己教学的问题，重要的是可以增加师生的感情，更会成为学生的益友。这样一堂课在师生共同的互动下就会变得轻松愉快。

二、适当的调节课堂气氛，提高学生的求知欲

课堂效率的提高，都离不开良好的课堂环境，对于内容比较抽象、枯燥的数学课来说，一个生动有趣的事例是必不可少的。让学生觉得数学来源于生活又用于生活，能够真正体验数学之奇，领悟数学之妙，从而激发学生学习数学的激情。

另外，创设情境可以使学生在探究数学问题的过程中体验和感受数学，使自己能够发现问题、分析问题、解决问题。

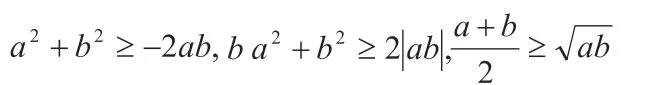
（2）试判断：

（3）在此基础上进一步理解、分析基本不等式应用的基本要求：一正、二定、三相等。构建一个阶梯性的问题情境就可以把一个较复杂的问题分成若干个相互联系且较易的子问题，这样学生就会感觉有层次，入手相对容易，也使得学生会产生“有梯可上，步步登高”的成就感，慢慢地学生就会形成自己有层次的思维空间，自己去分析理解问题。

三、课堂上尽量使题目开放化，提高学生思维能力

数学教学中把开放性题目引入课堂是对素质教育的一种探索，也是当前教育发展的一种潮流。开放性题目的教学能让学生从多方面、多层次探究、分析问题，提出新的见解，培养学生的创新意识和思维能力。

1.开放性题目的直接引入

例：直线y=2x+m 与抛物线交于A，B 两点，求直线AB 的方程。（要求补充恰当的条件，使直线方程得以确定）此题一出，学生的思维就活跃起来，学生补充的条件很多，例如：已知|AB|=m；若O 为原点，∠AOB=90；AB 中点的纵坐标为6；AB 过抛物线的焦点为F 等。

2.把应试题目开放化，多层变式，让学生从多个角度去思考问题

例如：已知函数f（x）=x3-3mx+1（a 不为0）。（1）求f（x）的单调区间；（2）若f（x）在x=1 处取得极值，直线y=ax 与y=f（x）的图像有三个不同的交点，求a 的取值范围。

在这第（2）问中，我们可以根据函数和方程的关系，把两个函数的交点转化为多个角度去思考,让学生展开想象的空间：

如果变形为一个方程，那么就是方程有几个根的问题，即：若f（x）在x=1 处取得极值，方程ax-f（x）=0 有三个不同的根，求a 的取值范围。

如果变为一个函数，那么就是函数零点的问题，即：若f（x）在x=1 处取得极值，函数y=ax-f（x）的图像有三个不同的零点，求a的取值范围。

如果转化为两个函数，那么就是函数交点的问题，也就是题目的问法：若f（x）在x=1 处取得极值，直线y=ax 与y=f（x）的图像有三个不同的交点，求a 的取值范围。

当遇到类似的问题时，学生可以灵活变通，试试哪种方法是最简单的，然后选取即可。

总之，提高课堂效率是每一位老师的教学任务，也是坚持研究的课题，更是一种价值追求，要构建高效的数学教学，切实提高教学效率，我们必须以先进的教学理论作指导，组织好课堂教学，充分调动学生学习的积极性和主动性，让学生学会自主学习、乐于探究，充分发挥他们的主体作用，最终使每位学生都能得到全面发展，能用他们独特的数学视角去观察世界，能用敏捷的数学思维去衡量社会，更能以充满希望的眼光去展望他们美好的未来！