三角函数综合演练B 卷
2019-05-28王能文
■王能文
一、选择题
1.一段圆弧的长度等于其圆内接正三角形的边长,则其圆心角的弧度数为( )。


4.点 P 从(1,0)出发,沿单位圆x2+y2=1逆时针方向运动弧长到达Q点,则Q点的坐标为( )。
6.由函数y=2cosx(0≤x≤2π)与函数y=2形成的封闭图形的面积大概是( )。
A.2 B.4
C.2π D.4π
7.已知函数f(x)=2sin(ωx+φ),x∈R,其中ω>0,-π<φ≤π。若f(x)的最小正周期为6π,且当时,f(x)取得最大值,则( )。
A.f(x)在区间[-2π,0]上是增函数
B.f(x)在区间[-3π,-π]上是增函数
C.f(x)在区间[3π,5π]上是减函数
D.f(x)在区间[4π,6π]上是减函数
8.已知函数y=2sin(ωx+φ)(ω>0,0<φ<π)的部分图像如图1所示,则φ=( )。
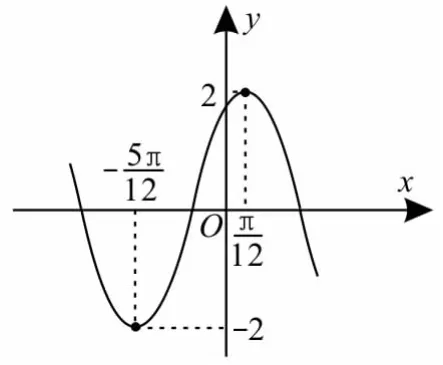
图1

9.已知f(cosx)=cos3x,则f(sin30°)的值为( )。

10.设f(x)=asin(πx+α)+bcos(πx+β),其中a,b,α,β都是非零实数,若f(2012)=-1,则f(2013)等于( )。
A.-1 B.0
C.1 D.2
11.下列函数中,最小正周期为π的偶函数是( )。
C.y=sin2x+cos2x
D.y=sinx+cosx
13.若函数fx()与gx()的图像有一条相同的对称轴,则称这两个函数互为同轴函数。下列四个函数中,与互为同轴函数的是( )。
A.gx()=cos(2x-1)
B.gx()=sinπx
D.gx()=cosπx


A.1 B.2
C.3 D.4
A.fx()的一个周期为-π
A.是奇函数
B.是偶函数
C.既不是奇函数也不是偶函数
D.既是奇函数又是偶函数
18.已知函数y=2sin(ωx+θ)为偶函数(0<θ<π),其图像与直线y=2的某两个交点的横坐标为x1,x2,且|x2-x1|的最小值为π,则( )。
19.若函数f(x)=3sin(2x+θ)(0<θ<π)是偶函数,则f(x)在[0,π]上的递增区间是( )。
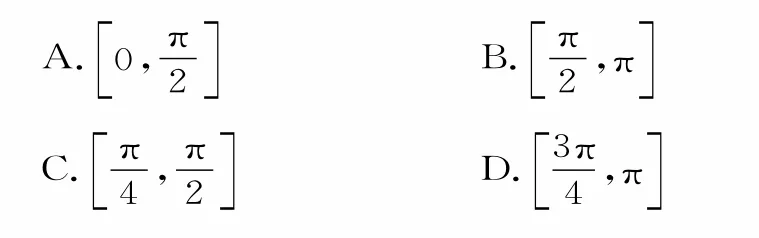
20.函数f(x)=Acos(ωx+φ)(A>0,ω>0,-π<φ<0)的部分图像如图2所示,为了得到g(x)=Asinωx的图像,只需将函数y=f(x)的图像( )。
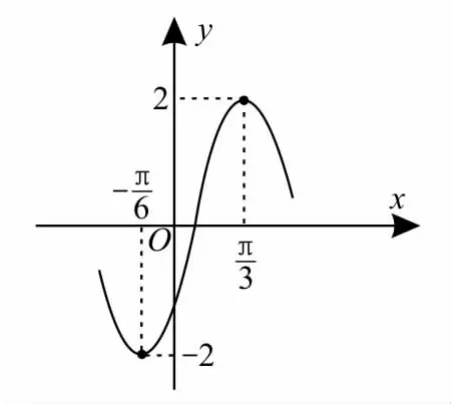
图2
①函数f(x)是偶函数;②函数f(x)的最小正周期为π;③函数f(x)在区间上是增函数;④函数f(x)的图像关于直线对称。
A.①② B.①②④
C.②③④ D.①②③
二、填空题
23.已知函数y=sin(ωx+φ)(ω>0,-π≤φ<π)的部分图像如图3所示,则φ=__________。
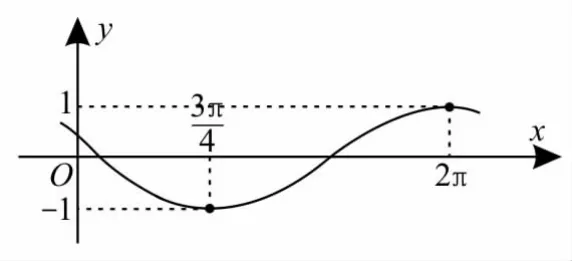
图3
25.函数f(x)=1+4cosx-4sin2x,x∈则f(x)的最小值为_______。
30.已知函数fx()=sin(ωx+φ)ω>0,0<φ<π()的周期为4,将函数f(x)的图像向右平移个单位后,所得图像关于原点对称,则函数y=f(x)在[0,1]上的值域为________。
三、解答题
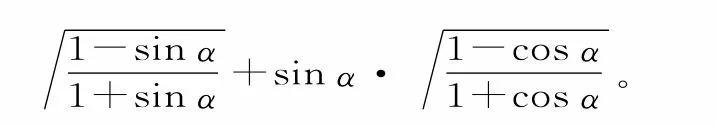
(1)化简f(α)。
(1)求函数f(x)的解析式。
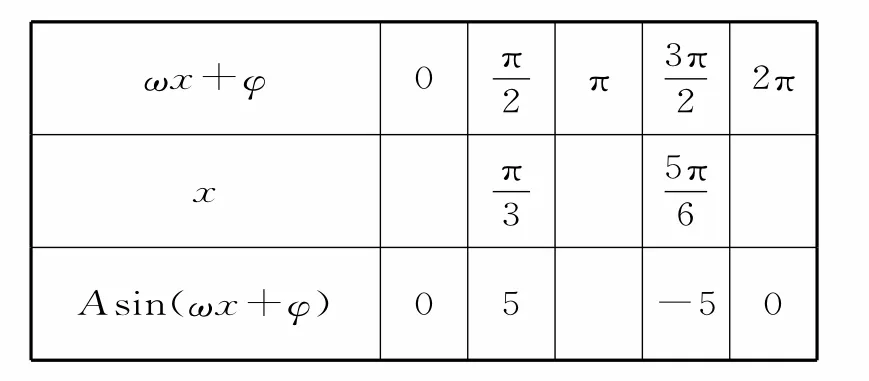
表1
(1)请将表中数据补充完整,并直接写出函数f(x)的解析式。
(2)将y=f(x)图像上所有点向左平行移动θ(θ>0)个单位长度,得到y=g(x)的图像。若y=g(x)图像的一个对称中心为求θ的最小值。
(1)求常数a,b的值。
(1)求fx()的值域和最小正周期。
37.已知函数f(x)=2sinωx,其中常数ω>0。
38.已知函数f(x)=sin2x+acosx+a,a∈R。
(1)当a=1时,求函数f(x)的最大值。
(1)求函数f(x)的解析式。
(2)将函数f(x)的图像向左平移1个单位后,纵坐标不变,横坐标伸长为原来的倍,得到函数g(x)的图像,求函数g(x)的单调递减区间。
