探究三角函数的图像与性质的重难点

■陈和改

三角函数的图像与性质的相关试题是近几年高考命题的热点，主要考查三角函数的定义域、最值、单调性、奇偶性和周期性等内容。下面分别介绍，以供大家参考。

一、三角函数的定义域问题

三角函数的定义域是研究三角函数的其他性质的前提，求三角函数的定义域，事实上就是求最简单的三角不等式，通常可用三角函数的图像来求解，体现了数形结合思想的应用。

例1求函数的定义域。

解：因为2sinx-1≥0，所以在同一坐标系内作出y=sinx，x∈[0，2π]和的图像（如图1所示），解方程sinx=得结合图像可以看出，满足的x的范围是故函数y 的定义域为

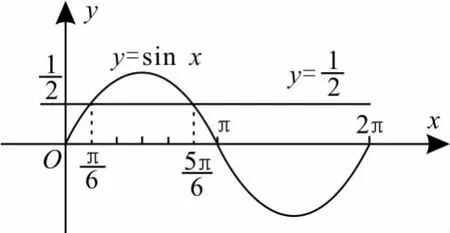
图1

对于三角不等式的求解，用常规方法求解有困难时，可以通过构造函数图像，使问题得以顺利解决。

跟踪练习1：求函数tanx）的定义域。

提示：因为所以故函数y的定义域为

二、三角函数的最值问题

求三角函数的最值主要有两种类型：一是将函数化为y=Asin（ωx+φ）+b的形式，利用三角函数的有界性，转化为不等式求最值问题；二是将函数化为y=psin2x+qsinx+r（p≠0）的形式，利用二次函数在给定区间上的特征求最值问题，此时应注意自变量的取值范围。

例2已知k＜-4，求函数y=cos2xsin2x+k（cosx-1）的最小值。

解：由题意得y=2cos2x+kcosx-k-因为k＜-4，所以所以当cosx=1时，函数y有最小值为ymin=1。

通过转化将三角函数问题转化为熟悉的二次函数在闭区间上的最值问题，使问题得以顺利解答。但用sinx或cosx表示函数时，一定要注意sinx，cosx的有界性。

跟踪练习2：求函数的最值。

提示：因为所以0≤2x+所以所以当时函数y有最大值为ymax=2；当时函数y有最小值为ymin=0。

三、三角函数的单调性问题

求函数y=Asin（ωx+φ）（A＞0，ω＞0）的单调区间的基本思路是把ωx+φ看成一个整体，求此函数的递增区间，就是解不等式Z）得到x的范围。若函数y=Asin（ωx+φ）（A＞0，ω＜0），可利用诱导公式将函数转化为则函数y=Asin（-ωx-φ）的单调递增区间为原函数的单调递减区间，单调递减区间为原函数的单调递增区间。

例3求函数的单调递减区间。

解：将函数转化为欲求该函数的单调递减区间，只需求函数y=的单调递增区间即可。由2kπ-解得kπ-故函数y的单调递减区间为

解决三角函数的单调性问题，关键是先利用诱导公式把x的系数化为正值，再求单调区间。

跟踪练习3：函数的单调递增区间为（ ）。

B.kπ，（k+1）π（），k∈Z

提示：函数的单调递增区间满足k∈Z，所以函数f（x）的单调递增区间为应选C。

四、三角函数的奇偶性问题

判断函数的奇偶性的主要方法是定义法，先看定义域是否关于原点对称，再看f（x）与f（-x）的关系。

例4判断函数fx（）=的奇偶性。

解：因为函数f（x）的定义域为R，且f（x）+f（-x）=lg1=0，所以f（-x）=-f（x）。所以函数f（x）为奇函数。

判断函数的奇偶性时，一般根据奇偶性的定义进行判断，在判断过程中有时也可由判断f（x）+f（-x）=0或f（x）-f（-x）=0得到结论。

跟踪练习4：判断函数fx（）=的奇偶性。

提示：因为函数f（x）的定义域关于原点对称，且f（-x）=f（x），所以函数f（x）为偶函数。

五、三角函数的周期性问题

函数的周期性的定义是对定义域中的每一个x值来说，都有f（x+T）=f（x）（T≠0），那么f（x）是以T为周期的函数。

例5下列函数中，周期为的是____。

解：由三角函数周期的定义可知，y=的周期为4π，y=tan2x的周期为的周期为8π，y=cos4x的周期为故答案为②④。

函数y=sinx的周期不止一个，如2π，4π，6π，…，事实上，任何一个非零常数2kπ（k∈Z）都是正弦函数的周期，2π只是y=sinx的最小正周期。

跟踪练习5：设点P 是函数f（x）=sinωx的图像C的一个对称中心，若点P到图像C的对称轴上的距离的最小值为则f（x）的最小正周期是（ ）。

提示：因为点P是函数f（x）=sinωx的图像C的一个对称中心，点P到图像C的对称轴上的距离的最小值为所以函数f（x）的最小正周期为应选B。

六、三角函数的对称性问题

正弦、余弦函数的图像都是轴对称与中心对称图形，其对称轴为过最值点且与x轴垂直的直线，分别为与x=kπ（k∈Z）；对称中心即为函数的零点，分别为（kπ，0）与正切函数的图像是中心对称图形，不是轴对称图形，其对称中心为函数的零点，即对称中心为

例6函数的图像的一条对称轴方程是（ ）。

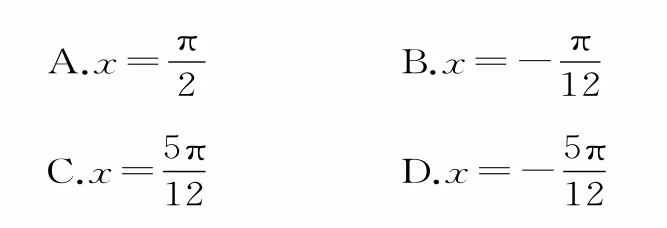
解：因为函数y=sinx的对称轴方程为所以由（k∈Z），得当k=-1时应选D。

跟踪练习6：函数的图像的一个对称中心是（ ）。

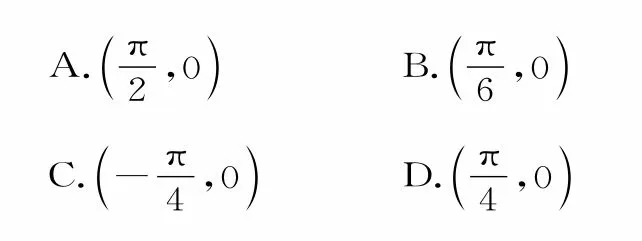
提示：因为函数y=cosx的对称中心是所以由得当k=0时应选D。

（纵坐标不变）

提示：先将函数y=2sinx，x∈R的图像上所有的点向左平移个单位长度，得到函数的图像。再把所得图像上各点的横坐标伸长到原来的3倍（纵坐标不变），得到函数x∈R的图像。应选C。