盘点三角函数最值问题的求法

■柯定尊

三角函数最值问题是近几年高考考查的一个重点，三角函数最值是函数最值的一个重要组成部分，与二次函数、不等式等内容紧密相关，由于其题型的变化多样，常常让同学们感到无从下手。下面介绍几种常见的求三角函数最值的方法，供同学们参考。

一、利用配方法求三角函数的最值

若函数表达式中只含正弦函数或余弦函数，且它们的次数是2时，一般需要通过配方或换元将给定的函数化归为二次函数的最值问题来处理。

例1求函数y=-2sin2x+2sinx+1的最值。

解：函数y=-2sin2x+2sinx+1=因为-1≤sinx≤1，所以当sinx=-1，即时当即时，ymax=-2×0+

解答本题的关键是先将函数式进行配方，再转化为二次函数求最值问题。

跟踪练习1：函数y=cos2x-3cosx+2的最小值为（ ）。

提示：函数y=cos2x-3cosx+2=因为-1≤cosx≤1，所以当cosx=1，即x=2kπ，k∈Z时，ymin=应选B。

二、利用归一法求三角函数的最值

若函数表达式中同时含有正弦函数和余弦函数，一般需要通过三角恒等变换将所给的函数式化为只含有一个函数名的形式。

例2求函数y=cos2x+5sinx-sin2x的最值。

解：函数y=1-sin2x+5sinx-sin2x=因为-1≤sinx≤1，所以当sinx=-1，即x=2kπ-k∈Z时，当sinx=1，即x=时

本题是利用三角函数的基本关系把函数的表达式转化为一个角的同名三角函数的形式进行求解的。

跟踪练习2：求函数y=sin2x+2cosx的最值。

提示：函数y=sin2x+2cosx=1-cos2x+2cosx=-（cosx-1）2+2。因为-1≤cosx≤1，所以当cosx=1，即x=2kπ，k∈Z时，ymax=2；当cosx=-1，即x=时，ymin=-4+2=-2。

三、利用有界性求三角函数的最值

在三角函数中，正弦函数和余弦函数具有一个最基本也是最重要的特征——有界性，利用正弦函数和余弦函数的有界性是求解三角函数最值的最基本的方法。

例3求函数的最值。

解：原函数变形为因为|sinx|≤1，所以所以-1≤y≤故函数y的最大值为最小值为-1。

跟踪练习3：求函数的值域。

提示：原函数变形为因为|cosx|≤1，所以所以y≥3或故函数y的值域为

四、利用单调性求三角函数的最值

如果一个三角函数通过换元后的函数在它的定义域上具有单调性，则可利用函数的单调性求最值。

例4已知x∈（0，π），求函数y=的最小值。

解：设sinx=t，因为x∈（0，π），所以0＜t≤1。所以在（0，1）上是减函数，所以当t=1时，函数y有最小值为3。

跟踪练习4：求函数 y=的值域。

提示：函数设sinx+2=t，因为sinx∈[-1，1]，所以1≤t≤3，所以y=t-在[1，3]上单调递增[图像类似对数函数，当x→0时，y→-∞，当x→+∞时，以y=x为渐 近线，且过点 （1，0）]。当t=1，即sinx=-1时，ymin=0；当t=3，即sinx=1时故函数y的值域为

五、利用数形结合法求三角函数的最值

由于sin2x+cos2x=1，所以从图形考虑，点（cosx，sinx）在单位圆上，这样对既含有正弦函数又含有余弦函数的三角函数的最值问题，可考虑用数形结合法求解。

例5求函数的最小值。

解：将函数表达式改写成y 可看成连接点A（2，0）与点（cosx，sinx）的直线的斜率。由于点（cosx，sinx）的轨迹是单位圆的上半圆，所以求y的最小值就是在这个半圆上求一点，使得相应的直线斜率最小。设过点A的切线与半圆相切于点B，则kAB≤y＜0，可求得所以函数y的最小值为

跟踪练习5：求函数的最大值。

提示：由函数设点P 为（sinx，cosx），点Q 为（-2，0），则可看成是单位圆上的动点P与点Q连线的斜率，如图1所示。设过点Q的切线与圆相切于点P1时，直线的斜率最大。可求得所以可得y=1。所以函数y的最大值为1

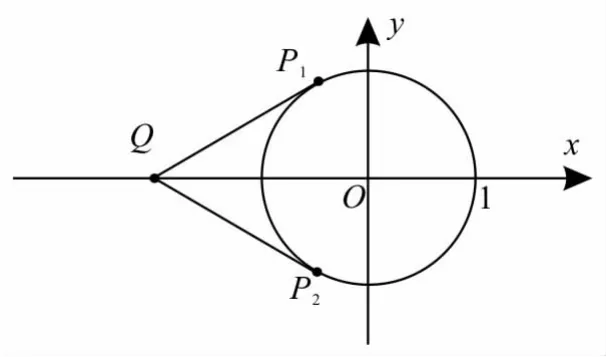
图1

六、利用分类讨论法求三角函数的最值

对于含参数的三角函数的最值问题的解答，往往需要对参数进行分类讨论。

例6 设函数f（x）=cos2x+asinx-用a表示f（x）的最大值 M（a）。

解：函数f（x）=-sin2x+asinx-令sinx=t，则0≤t≤1，故g（t）=

本题主要利用换元法将原函数转化为关于sinx的二次函数，根据sinx的取值范围[-1，1]，利用对称轴进行分类讨论求出最大值。

跟踪练习6：求关于x的函数y=-sin2x-2asinx+1-a的最大值。

提示：函数y=-sin2x-2asinx+1-a=-（sinx+a）2+a2-a+1。令sinx=t，则|t|≤1，故y=-（t+a）2+a2-a+1。

（1）若-1≤-a≤1，即-1≤a≤1，则t=-a时，函数y有最大值为ymax=a2-a+1（如图2所示）。

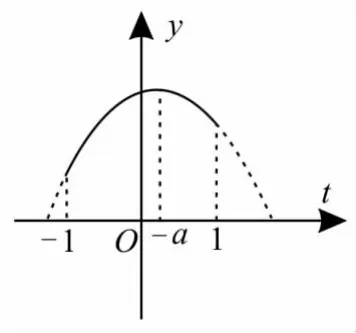
图2

（2）若-a＜-1，即a＞1，则t=-1时，函数y有最大值为ymax=a（如图3所示）。

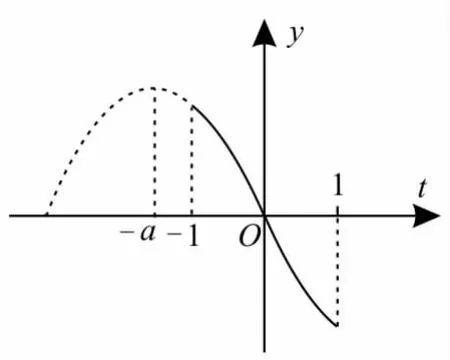
图3

（3）若-a＞1，即a＜-1，则t=1时，函数y有最大值为ymax=-3a（如图4所示）。

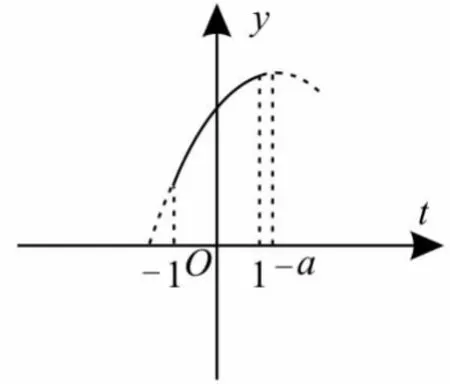
图4