揭秘三角函数的图像与应

■周湘林

作三角函数的图像一般有两种方法，一是五点作图法，二是图像变换法。利用三角函数的图像变换，不仅方便画出三角函数的图像，而且还可以进一步研究三角函数的性质。下面就让我们一起来揭秘三角函数的图像及其应用吧！

一、五点法作简图

用五点法作正弦、余弦型函数图像的步骤：①将原函数化为y=Asin（ωx+φ）（A＞0，ω＞0）的形式；②确定周期；③确定一个周期内函数图像的最高点和最低点；④选出一个周期内与x轴的三个交点；⑤列表；⑥描点画图。

例1用五点法画出函数y=的图像，并指出这个函数的周期与单调区间。

解：令则按五个关键点列表，如表1所示。

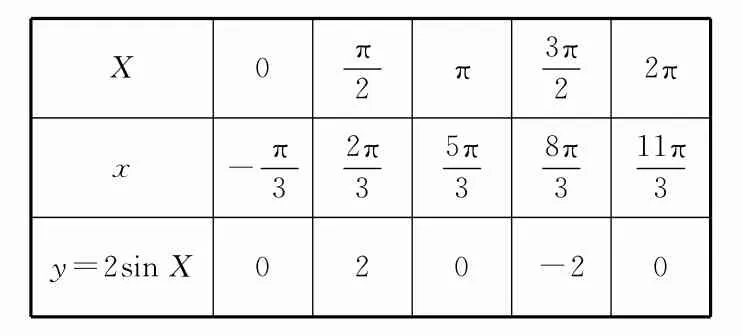
表1

先在坐标系中描出相应的五点，再用光滑的曲线连接起来，如图1所示，最后向两端伸展一下。

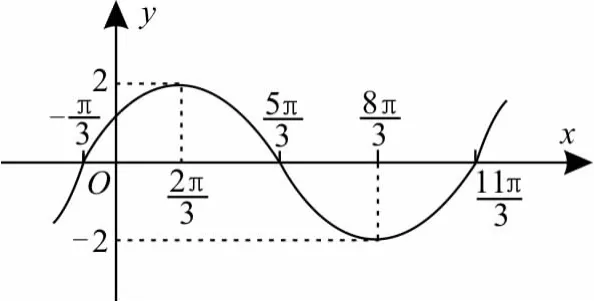
图1

运用五点法作函数y=Asin（ωx+φ）（A＞0，ω＞0）的简图时，通常把ωx+φ看成一个整体，按五个关键点列表（如表2所示）。在坐标系中描出五个关键点并将它们用光滑的曲线连接起来，要注意曲线的凹凸方向，从而可以画出函数在一个周期内的简图。

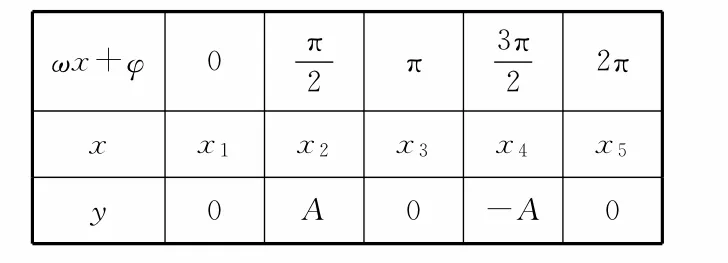
表2

跟踪练习1：用五点法作出函数y=在一个周期内的图像。

提示：令解得令解得解得令解得令解得按五个关键点列表，如表3所示。

表3

描点并将它们用光滑的曲线连接起来，得到函数的图像，如图2所示。

图2

二、三角函数的图像变换问题

由函数y=sinx的图像经过变换得到函数y=sin（ωx+φ）的图像，有两种主要途径：一是先左右平移后伸缩横坐标，即y=sinx→y=sin（x+φ）→y=sin（ωx+φ）；二是先伸缩横坐标后左右平移，即y=sinx→y=sin（ωx）→y=sin（ωx+φ）。大家要注意的是，第一种途径平移|φ|个单位长度，第二种途径平移个单位长度。

例2为了得到函数的图像，只需把函数y=sin2x的图像（ ）。

解决平移问题，要遵循“只对x，y 进行运算”的原则，因此，对于将函数y=sin（ωx）（ω≠1）的图像平移得到函数y=sin（ωx+φ）（ω≠1）的图像问题，先要把函数y=sin（ωx+φ）（ω≠1）的解析式写成的形式，再进行平移变换，才能使问题得以顺利解答。

跟踪练习2：为了得到函数y=的图像，只需把函数y=的图像（ ）。

提示：函数函 数所以将函数的图像向右平移个长度单位，即可得到函数的图像。应选B。

例3为了得到函数的图像，只需把函数y=cos2x的图像（ ）。

解答函数图像的平移问题时，要注意平移前后两个函数的解析式的函数名是否相同。如果函数名不同，应先化为同名函数，再进行平移变换。

跟踪练习3：将函数的图像向左平移个单位长度后，所得图像对应的函数是偶函数，则φ=________。

提示：将函数的图像向左平移φ个单位长度后，得到函数y=的图像。因为函数y=是偶函数，所以解得又因为所以

三、求三角函数的解析式

确定函数y=Asin（ωx+φ）的解析式，就是确定其中的参数A，ω，φ的值。从图像的特征寻找答案，A由最值确定；ω由周期确定，周期一般通过特殊点观察求得，如相邻的最高点、最低点的横坐标相差半个周期；φ可由点在函数图像上列方程求得，确定φ值时，注意它的不唯一性，一般求|φ|中最小的φ值。

例4图3所示的是函数y=Asin（ωx+φ）的图像，请确定 A，ω，φ 的值，并确定函数的解析式。

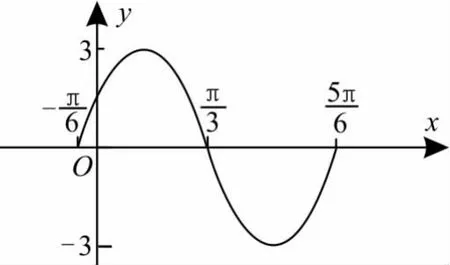
图3

解法1：（代入法）由图像知A=3，由T=可得因为图像过点令得所以此函数的解析式为

解法2：（五点法）由图像知A=3，且图像过点根据五点作图法的原理，可得

通过将若干个特殊点代入函数式，可以求得相关参数A，ω，φ的值。这里需要注意的是，所选择的点属于五点法中的哪一个点，并要正确代入列出等式。

跟踪练习4：如图4所示，函数y=Asin（ωx+φ）（A＞0，ω＞0）的图像上相邻的最高点与最低点的坐标分别为和求该函数的解析式。

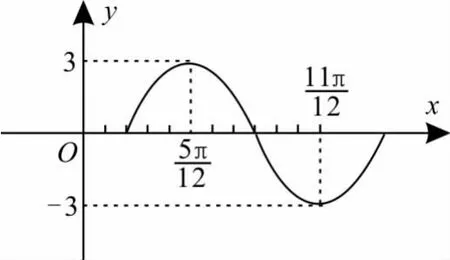
图4

提示：依题意知，A=3。因为所以T=π。又因为所以ω=2。这时函数的解析式为y=3sin（2x+φ）。由图像过点和根据五点作图法的原理，可得解得ω=所以此函数的解析式为y=