小议三角函数问题中的求参数的方法

■税建华

求解三角函数中的参数问题，需要熟练掌握三角函数的性质，这类问题可利用方程思想与待定系数法相结合求解。

一、根据三角函数的奇偶性求参数

解：先求出f（x+φ）的解析式，然后求φ的值。由可得f（x因为函数f（x+φ）为偶函数，所以即

评析：函数y=Acos（ωx+φ）+B（A≠0）为奇函数且B=0。函数y=Acos（ωx+φ）+B（A≠0）为偶函数⇔φ=kπ（k∈Z）。

例2函数sin（3x-θ）是奇函数，则tanθ=__________。

解：根据f（0）=0可求得tanθ的值。因为函数f（x）的定义域为R，且f（x）为奇函数，所以f（0）=0，即=0（使cosθ=0的θ值不满足题设条件，故cosθ≠0），可得

评析：若函数f（x）是R上的奇函数，则f（0）=0。

二、根据三角函数的单调性求参数

例3已知函数f（x）=-2sin（2x+φ）（|φ|＜π），若是f（x）的一个单调递增区间，则φ的取值范围为（ ）。

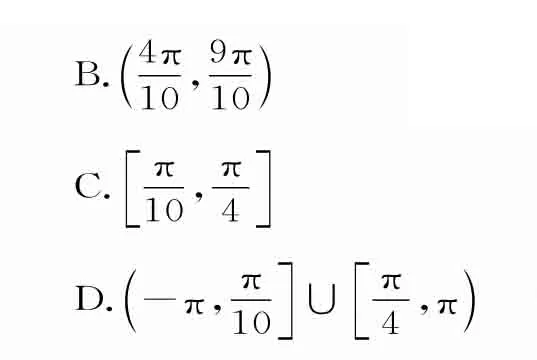
解：先求出已知函数的单调递增区间，使为其子区间即可求得φ的取值范围。因为Z，所以Z。因为是f（x）的一个单调递增区间，且|φ|＜π，所以解得同理由可得由上可得应选C。

评析：此类问题要注意单调区间给出的方 式，如 “函 数 f （x）在上单调递增”与“函数f（x）的单调递增区间为Z）”这两者是不相同的。

例4将函数0）的图像向左平移个单位，得到函数y=g（x）的图像，若y=g（x）在上为增函数，则ω的最大值为__________。

解：利用平移变换求出函数g（x）的解析式是解题的关键。由题意可得g（x）=可知g（x）的增区间为即又x∈所以ω≤2。故ω的最大值为2。

评析：把函数f（x）=sinx的图像向右平移φ（φ＞0）个单位长度，只需用x-φ代替f（x）=sinx 中的x 即可；把函数f（x）=sinx的图像向左平移φ（φ＞0）个单位长度，只需用x+φ代替f（x）=sinx中的x即可。

三、根据三角函数的周期性求参数

例5函数f（x）=sinωx（ω＞0）图像的相邻两条对称轴之间的距离为2，则ω=__________。

解：因为f（x）图像的相邻两条对称轴之间的距离为2，所以T=4，可得即

评析：在解决由三角函数图像确定函数解析式的问题时，要注意充分利用函数图像显示出来的函数性质。

四、根据三角函数的图像平移求参数

例6函数y=cos（2x+φ）（-π≤φ＜π）的图像向右平移个单位长度后，与函数的图像重合，则φ=__________。

解：将y=cos（2x+φ）的图像向右平移个单位长度后得到函数y=的图像。

评析：解答本题的关键是平移后两个函数的名称要一致，即平移后两个函数为同名三角函数。

五、根据三角函数的零点求参数

例7已知函数y=Asin（ωx+φ）（A＞的图像的一部分如图1所示，则f（x）的表达式为___________。

图1

解：由图像可知A=2。因为点（0，1）在图像上，所以1=2sin（ω·0+φ），即sinφ=又所以

评析：解决这类问题，一般是先根据图像的最高点与最低点确定A的值，由函数的周期确定ω的值，再根据函数图像上的一个特殊点确定φ的值。

六、根据三角函数的最值求参数

评析：解答本题的关键是辅助角公式的灵活应用。