含隧道边坡水平屈服加速度的上限分析

江学良，牛家永，杨 慧，王飞飞

(1.中南林业科技大学 土木工程与力学学院，长沙 410004；2.中南林业科技大学 岩土工程研究所，长沙 410004)

下伏隧道的边坡结构形式[1]频繁地出现在我国地震频发的西南山区中，尤其在2017年8月8日四川九寨沟县发生7.0级地震后，含隧道边坡的地震稳定性问题逐渐成为岩土工程中的研究热点[2]。

在含隧道边坡的地震动力稳定性分析中，确定其屈服加速度是一个重要研究内容。近年来，大量学者基于拟静力法对地震作用下边坡的屈服加速度进行了极限分析[3-4]。文畅平[5]采用塑性极限分析上限定理和正交试验法，对多级支护边坡屈服加速度及因素敏感性进行分析，给出了地震作用下基覆边坡水平屈服加速度系数影响因素的敏感性顺序。王桂林等[6]将挡土墙和填土看成一个系统，推导了重力式挡土墙在旋转位移下的水平屈服加速度系数理论计算公式。罗渝等[7]根据极限分析上限定理并结合多块体速度场理论，建立地震作用下边坡地震屈服加速度的多元函数，提出了一种计算重力式挡墙加固边坡动力稳定性的新方法。肖世国等[8]基于极限分析上限定理，推导了边坡地震屈服加速度计算公式，并结合 Newmark滑块位移法推导了坡体地震永久位移的详细计算公式。年廷凯等[9]结合拟静力法和极限分析法，推导了多排锚加固复杂边坡的稳定性安全系数和屈服加速度系数解析式，提出了锚固土质边坡地震稳定性的通用极限分析上限方法。陈春舒等[10]基于极限分析原理，考虑了滑坡体下滑转角和边坡几何参数的影响，推导了边坡实时屈服加速度系数、实时角加速度以及震后水平位移的计算表达式。

上述成果仅针对不含隧道的支护结构与边坡系统[11]，目前很少有学者针对含有隧道的边坡进行极限分析[12]，关于含隧道边坡的屈服加速度研究更是未见文献报道，有关其地震稳定性及结构计算方面的理论远没有跟上工程建设的步伐[13]，基于此，本文结合拟静力法[14]，强度折减法和极限分析上限定理，构建含隧道边坡的破坏模式，以期推导其水平屈服加速度的计算公式。在此基础上，对主要影响因素进行敏感性分析。

1 极限分析上限法

极限分析上限法是常用的稳定性极限分析方法，在边坡稳定性问题中应用广泛，可以叙述为在所有机动容许的塑性变形位移速度场相对应的荷载中，极限荷载最小。其特点是需要构造合适的破坏模式和速度场，破坏模式一般由刚塑性体体系构成，刚塑性体间由滑动面(速度间断线)隔开，整个刚塑性体体系的运动方式需满足上限定理要求的塑性流动和速度相容条件。对于任意机动容许的破坏机制，其外力功率不大于内能耗散功率。外力功率一般包括由岩土体重力、孔隙水压力、边坡超载以及地震荷载所做的功率。内能耗散功率则包括破坏面内能耗散功率和支护结构抗力所做的功率。

1.1 基本假定

在参考相关研究成果的基础上，为了便于分析作出如下基本假定：

①该岩质边坡为各向同性的均质软岩边坡；②隧道围岩视为理想弹塑性体，且服从Mohr-Coulomb屈服准则的c-φ材料；③破坏面为对数螺旋线破坏面，通过坡趾并穿过隧道；④将含隧道边坡稳定性分析简化为平面应变问题；⑤将隧道简化成圆形截面进行计算，作用在隧道拱顶的竖向围岩压力简化为线性均布荷载q，作用在边墙处的水平围岩压力简化为线性均布荷载e；⑥岩土体材料的抗剪强度参数不随地震作用而产生变化，并用拟静力法分析地震效应。

1.2 破坏机构

构建合理的破坏模式是极限分析上限法的前提和关键。运用MIDAS GTS/NX的强度折减法分析模块模拟含隧道边坡的破坏模式，图1为含隧道边坡的等效应变云图。由图1可知滑移面由坡脚穿过隧道的左边墙和右拱肩，向上延伸至接近坡顶处。这与文献[15]所给出的空区在边坡内的最不利位置相同，当空区在滑动带上时，边坡的稳定性相比于空区完全处于滑动带内和空区完全处于滑动带外时最弱。参考相关文献[16]，对数螺旋线破坏面与实际破坏面相一致，其满足运动许可速度场的破坏模式与实际破坏模式较为接近，所以本文采用对数螺旋线破坏机构。

图1 含隧道边坡等效应变云图Fig.1 Equivalent effective strain nephogram of slope with tunnel

本文采用如图1所示的对数螺旋线破坏机构，其破坏面穿过隧道的左边墙C点和右拱肩B点，隧道半径为R，O′点至坡脚D点的水平和竖直距离分别为d1和d2。将ABCDA′A区域视为刚塑性体，以角速度Ω绕旋转中心O(尚未确定)相对对数螺旋面AD以下的静止材料作刚体旋转，因此AD面为本文研究的破坏机制的速度间断面。基准线OA、OD的长度和倾角分别为r0、θ0和rh、θh，直线OB、OC的长度和倾角分别为rB、θB和rC、θC。整体破坏机构的高度为H，坡顶距离隧道右拱肩B点的垂直高度为α3H，B点和C点的垂直高度为α2H，隧道左边墙C点距离坡脚D点的垂直高度为α1H，其中α1，α2和α3为高度系数，可由方程组(3)确定，A′A长度为L。破坏机构由θ0，θh和β确定。

对数螺旋曲线方程可表示为[17]

r(θ)=r0·exp[(θ-θ0)·tanφ]

(1)

式中：φ为滑动面上任一点处的应变速度矢量V与该点处的滑动线所成的夹角，即围岩的内摩擦角(°)。r，θ分别为滑动面上任一点与O点连线的长度和倾角。则基准线OD的长度为

rh=r0·exp[(θh-θ0)·tanφ]

(2)

(3)

根据图2中的几何关系可得

H=rhsinθh-r0sinθ0

(4)

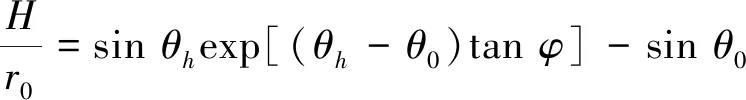
(5)

L=r0cosθ0-rhcosθh-Hcotβ

(6)

(7)

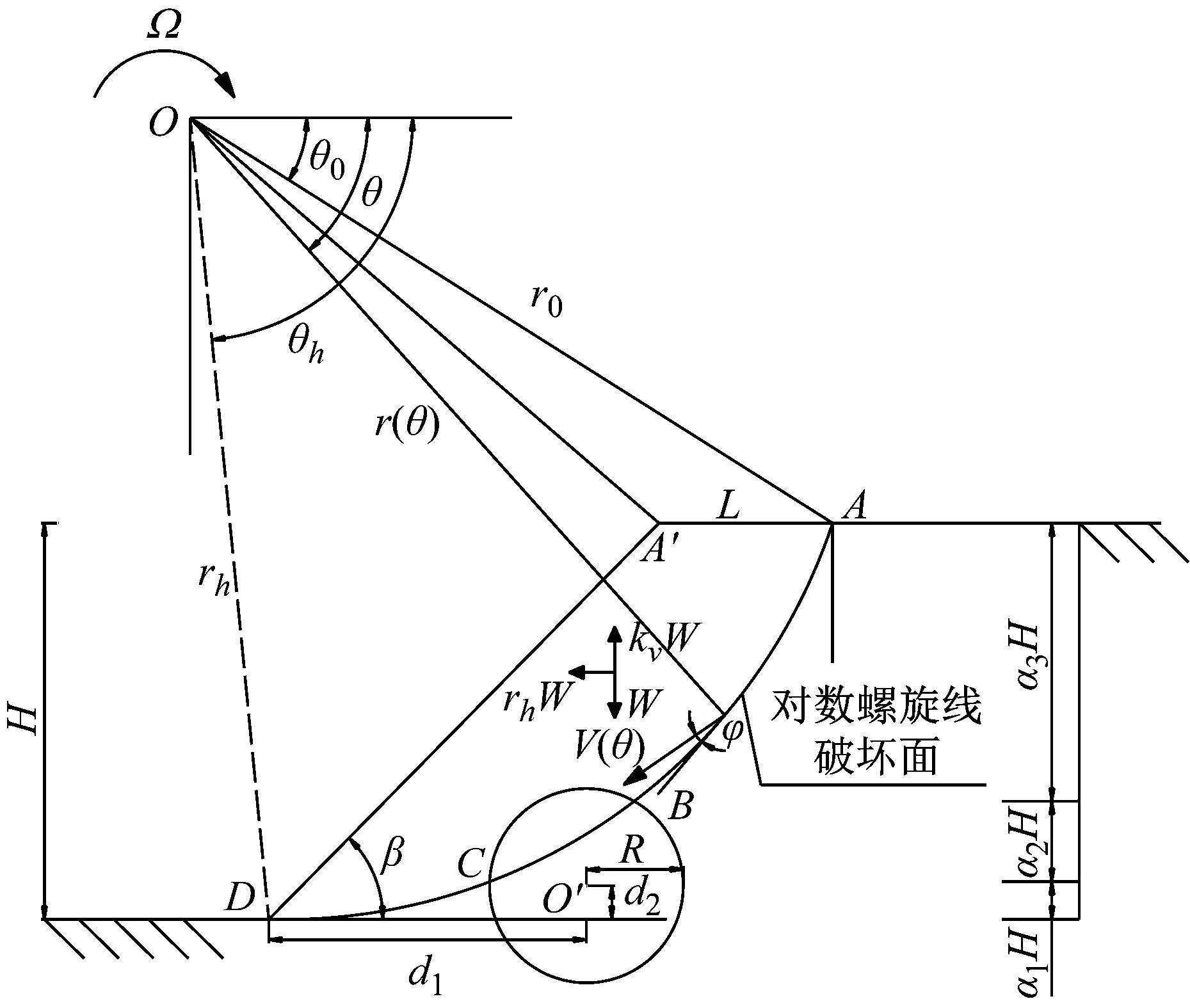
图2 含隧道边坡对数螺旋线破坏机构Fig.2 Log-spiral failure mechanisms of slope with tunnel

2 上限分析能耗计算

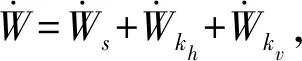
2.1 外力功率

2.1.1 岩土体重力做功功率

(8)

式中：γ为土的重度(kN·m-3)。f1～f4为关于(θh，θ0)的函数，见式(9)～(12)。

图3为各对数螺旋线BCC′区域的计算详图。因为其岩土体区域相对于整体旋转区域较小，故将BCC′区域简化为梯形求解该区域岩土体的重力做功功率。

exp[3(θh-θ0)tanφ]-3tanφcosθ0-sinθ0}

(9)

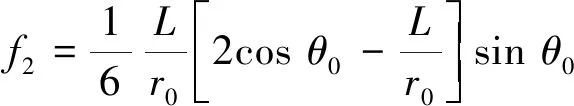
(10)

(11)

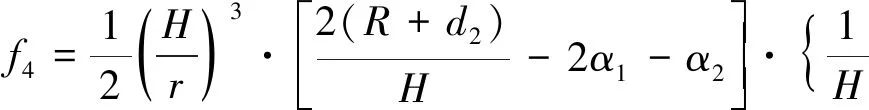
exp[(θh-θ0)tanφ]·cosθh-

(12)

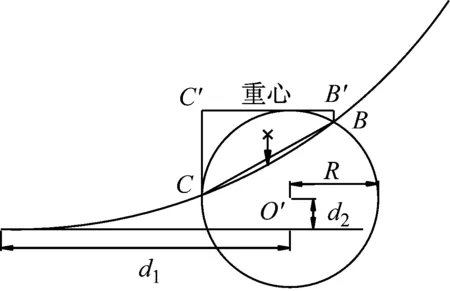
图3 函数f4的详细计算图Fig.3 Detailed calculations of function f4

2.1.2 地震惯性力做功功率

(13)

(14)

式中：参数f1，f2，f3及f4同上，f5～f8为关于(θh，θ0)的函数，见式(15)～(18)。

exp[3(θh-θ0)tanφ]-3tanφsinθ0+cosθ0}

(15)

(16)

(17)

(R+d2-α1H-α2H)·(R+d2-α1H)+

(18)

所以外力做功的总功率为

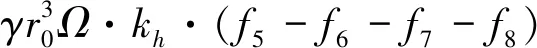
(19)

令F1=f1-f2-f3-f4，F2=f5-f6-f7-f8，则式(19)变为

(20)

2.2 内能耗散功率

2.2.1 速度间断面上的能量耗散

边坡发生塑性破坏时，可认为刚塑性区ABCDA′A内部不发生功率耗散并且局部变形基本一致，速度间断面AD上的能量耗散可通过积分由下式计算

(21)

式中：c为土体黏聚力(MPa)，Vcosφ为跨间断面的切向间断速度，其他参数同上。

(22)

2.2.2 衬砌抗力功率

因对数螺旋破坏面穿过隧道，故仅考虑对数螺旋面上方岩土体的垂直和水平围岩压力。衬砌结构上所承受的力可以看作围岩压力，由于衬砌结构阻止围岩发生破坏，故衬砌抗力所做的功率与围岩压力做的功率大小相等，符号相反。假定垂直围岩压力合力作用点在B′、C′水平距离的中点，水平围岩压力合力作用点分别在BB′点和CC′的中点。

(23)

(24)

式中：Fq为竖向围岩压力，Fel，Fer分别为隧道左右两侧的水平围岩压力。f10,、f11和f12为关于(θh，θ0)的函数，见式(25)、(26)和(27)。

(25)

(26)

(27)

总衬砌抗力做功为

r0Ω·(Fqf10+Felf11-Ferf12)

(28)

因此，总的内能耗散功率为

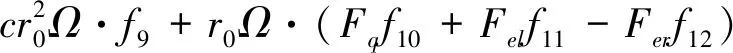
(29)

由极限分析上限定理可知，当外力功率等于内能耗散功率，即可求得含隧道边坡的水平屈服加速度上限解。

(30)

将式(20)、(29)，以及kv=akh(a为水平和竖向地震力比例系数)代入式(30)，整理可得式(31)

(31)

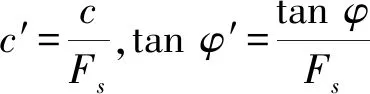
(32)

3 影响因素敏感性分析

3.1 影响因素正交分析

含隧道边坡水平屈服加速度的影响因素主要有边坡设计参数，边坡岩土体物理力学参数，浅埋偏压隧道设计参数和地震荷载参数。为了简化分析，选取以下7个因素进行正交分析：边坡高度H，坡角β，岩土体的强度折减系数Fs，黏聚力c，隧道距坡脚的距离d1，隧道半径R，水平和竖向地震力比例系数a。根据实际工程设计经验，每个因素取3个水平，每个水平对应9组试验，不考虑各因素之间的交互作用，布置在L27(37)正交试验表中用于正交试验分析[18]。其它因素在计算时取：γ=20 kN/m3，φc=50°，α1=0.1，α2=0.2，α3=0.7，d2=4 m。正交试验方案表如表1和表2所示。以每个因素的每一个水平所对应的ky平均值作为该因素的水平屈服加速度临界值，进行各因素的极差分析。正交试验极差分析表如表3所示。

表1 正交试验方案表Tab.1 Table of orthogonal test scheme

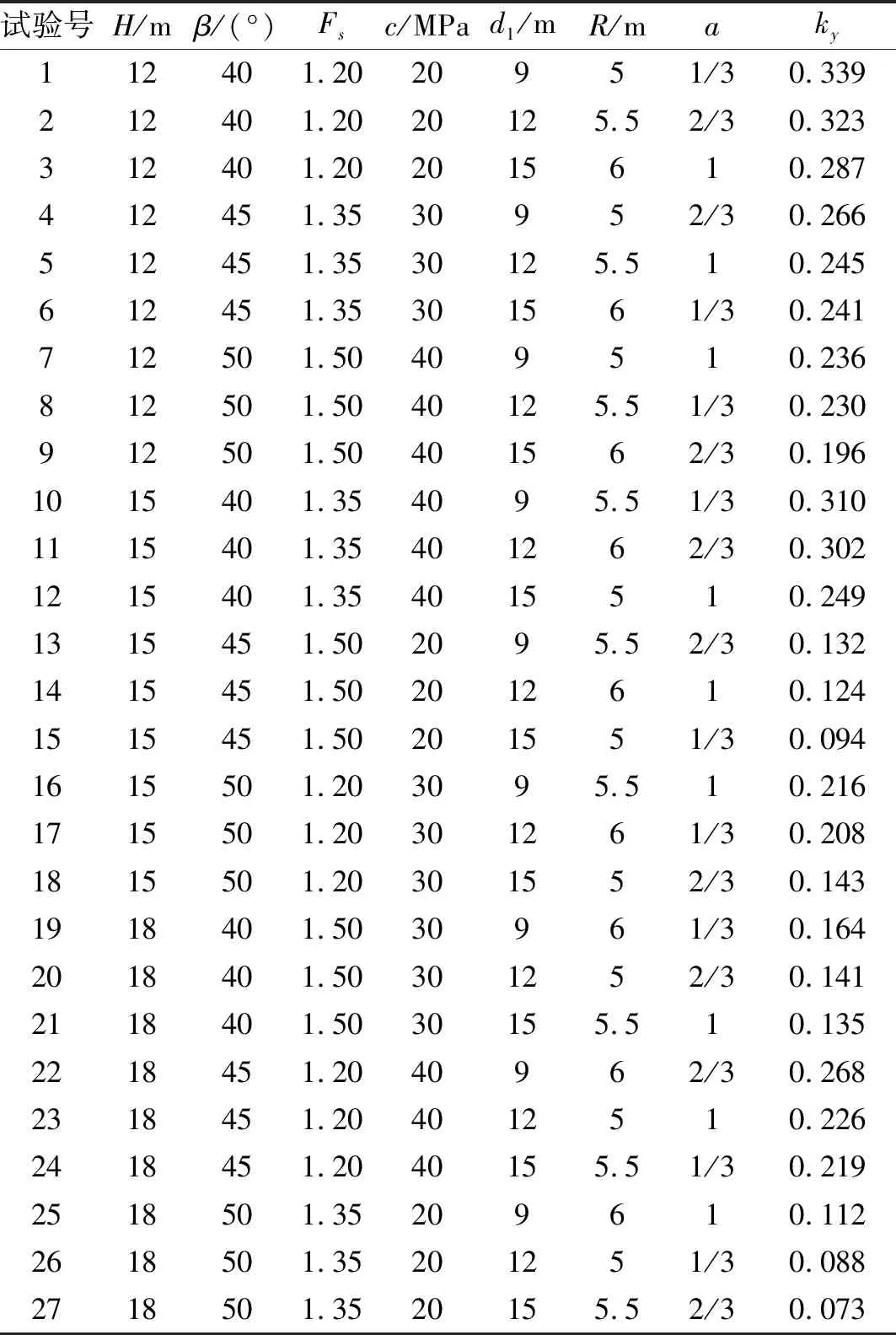
表2 正交试验表Tab.2 Table of orthogonal tests

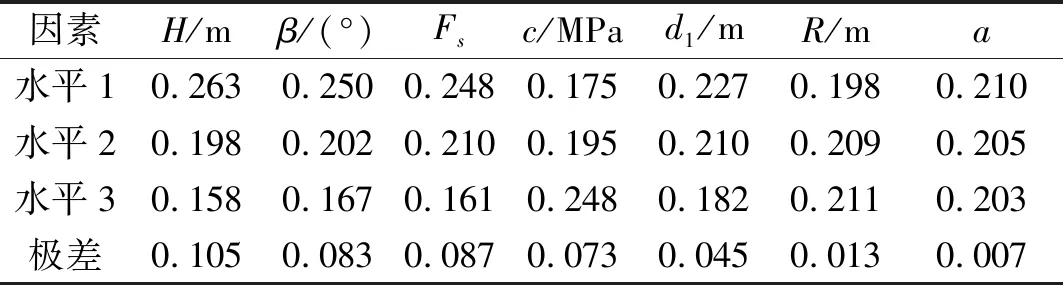
表3 正交试验极差表Tab.3 Range of orthogonal test

极差越大表示试验结果对该因素的敏感性越大。由表3可知，以上7个影响因素的敏感性大小依次为：H>Fs>β>c>d1>R>a。其中，水平屈服加速度对边坡高度H，坡角β和岩土体的强度折减系数Fs的敏感性较大，对隧道距坡脚的距离d1，隧道半径R，水平和竖向地震力比例系数a的敏感性则较小。

3.2 水平屈服加速度影响因素分析

采用控制变量法[19]对以上7个影响因素进行研究。计算的基本参数为：H=15 m，β=45°，φ=30°，c=30 kPa，γ=20 kN/m3，φc=50°，α1=0.1，α2=0.2，α3=0.7，d1=12 m，d2=4 m，R=5 m，Fs=1.2，a=1/3。

计算时分别取β=40°、45°、50°、55°和60°，其他参数不变。图4给出了水平屈服加速度随坡角的变化规律。随着坡角的增加，水平屈服加速度系数呈现近似线性减小的趋势。

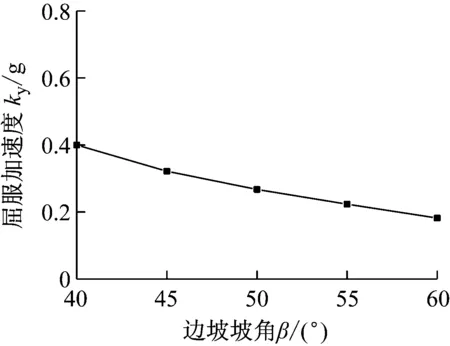
图4 水平屈服加速度系数随坡脚的变化规律Fig.4 Change law of the horizontal yield acceleration coefficient with the slope angle

计算时分别取Fs=1.0、1.2、1.4、1.6和1.8，其他参数不变。图5给出了水平屈服加速度随强度折减系数的变化规律。随着强度折减系数的增加，水平屈服加速度系数呈现非线性减小的趋势。

图5 水平屈服加速度系数随强度折减系数的变化规律Fig.5 Change law of the horizontal yield acceleration coefficient with the shear strength reduction coefficient

计算时分别取H=9 m、12 m、15 m、18 m和21 m，其他参数不变。图6给出了水平屈服加速度随边坡高度的变化规律。随着边坡高度的增加，水平屈服加速度系数呈现非线性减小的趋势。相较于坡角和强度折减系数，边坡高度的ky变化幅度最大，说明边坡高度对水平屈服加速度系数的影响程度最大，坡角和强度折减系数的影响次之。

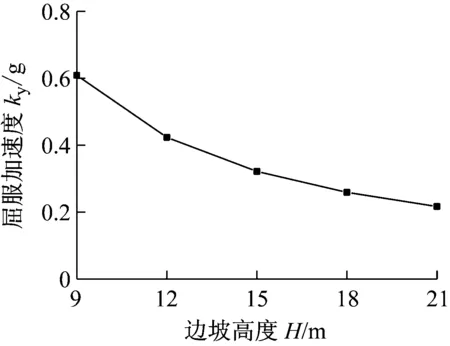
图6 水平屈服加速度系数随边坡高度的变化规律Fig.6 Change law of the horizontal yield acceleration coefficient with the height of slope

计算时分别取c=20 kPa、25 kPa、30 kPa、35 kPa和40 kPa，其他参数不变。图7给出了水平屈服加速度随黏聚力的变化规律。随着黏聚力的增加，水平屈服加速度系数呈现近似线性增大的趋势，其变化幅度适中，说明黏聚力对水平屈服加速度系数有一定影响。

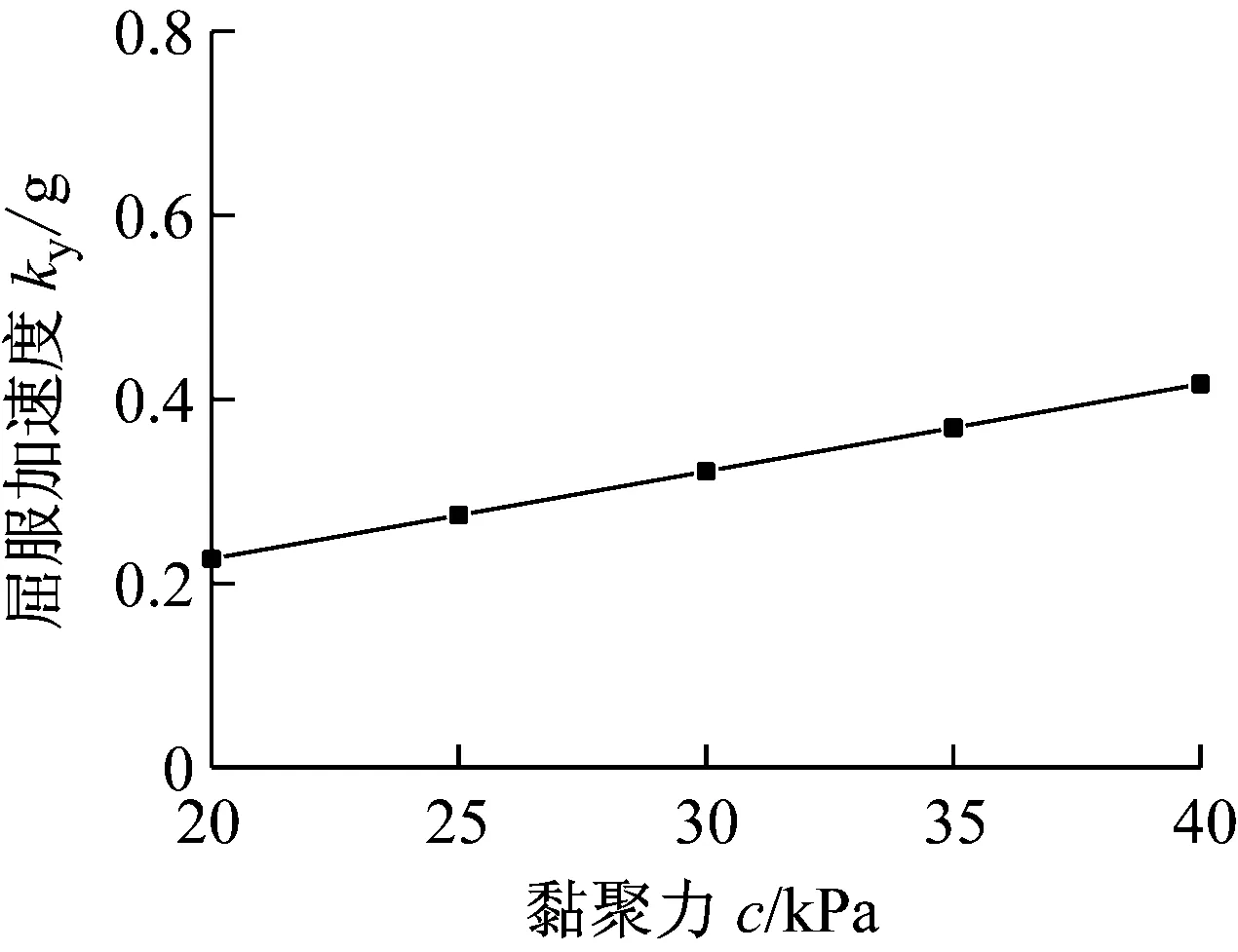
图7 水平屈服加速度系数随黏聚力的变化规律Fig.7 Change law of the horizontal yield acceleration coefficient with the cohesion

计算时分别取d1=9 m、11 m、13 m、15 m和17 m，其他参数不变。图8给出了水平屈服加速度随隧道距坡脚距离的变化规律。随着隧道距坡脚距离的增加，水平屈服加速度系数呈现近似线性减小的趋势，其变化幅度较小，说明隧道距坡脚距离对水平屈服加速度系数影响较小。

图8 水平屈服加速度系数随隧道距坡脚距离的变化规律Fig.8 Change law of the horizontal yield acceleration coefficient with the distance between the tunnel and the slope foot

计算时分别取R=4 m、4.5 m、5 m、5.5 m和6 m，其他参数不变。图9给出了水平屈服加速度随隧道半径的变化规律。随着隧道半径的增加，水平屈服加速度系数呈现近似线性增大的趋势，其变化幅度很小，说明隧道半径对水平屈服加速度系数影响很小。

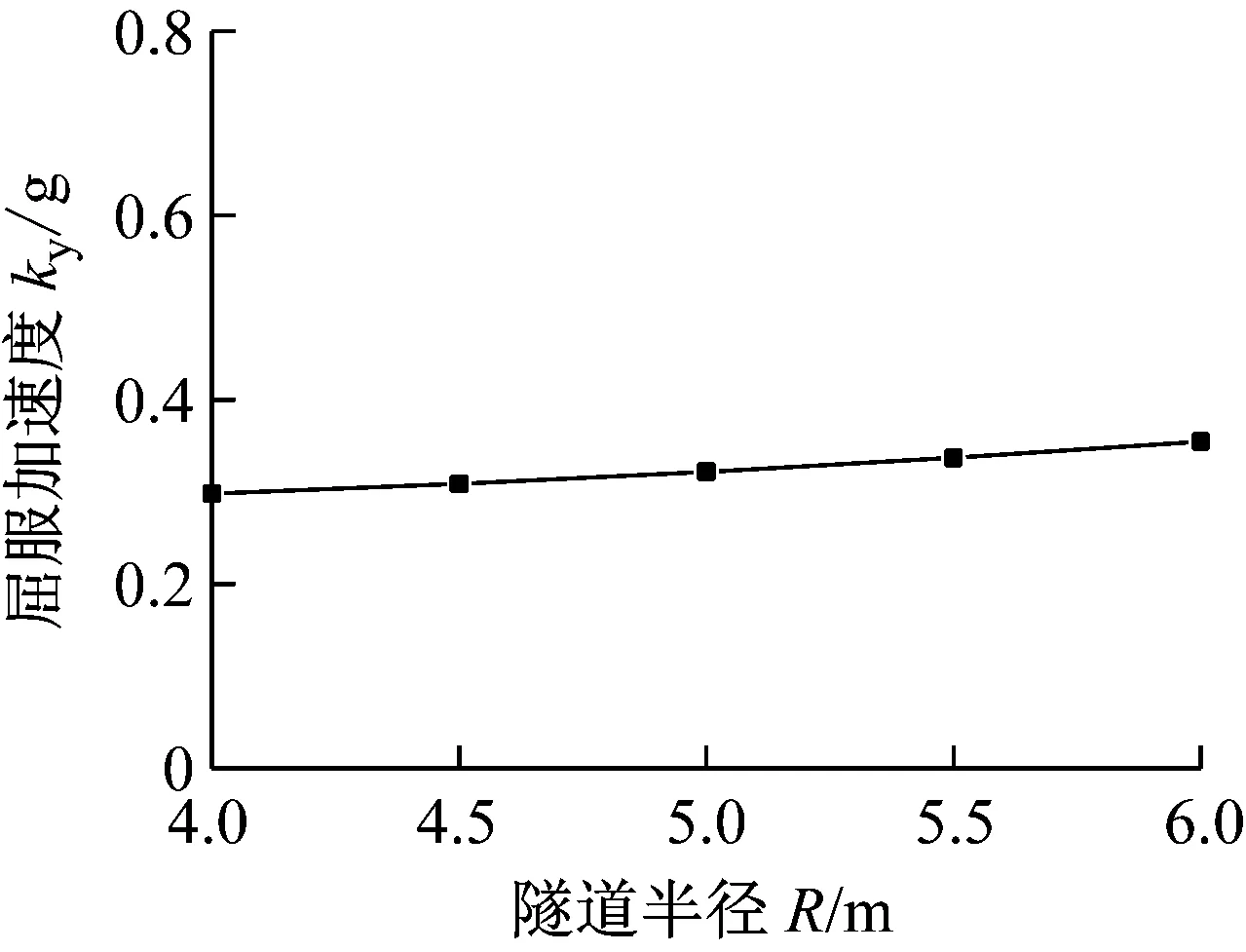
图9 水平屈服加速度系数随隧道半径的变化规律Fig.9 Change law of the horizontal yield acceleration coefficient with the tunnel radius

计算时分别取a=0、1/3、1/2、2/3和1，其他参数不变。图10给出了水平屈服加速度随水平和竖向地震力比例系数的变化规律。随着地震力比例系数的增加，水平屈服加速度系数呈现近似线性减小的趋势，其变化幅度很小，说明地震力比例系数对水平屈服加速度系数影响很小。

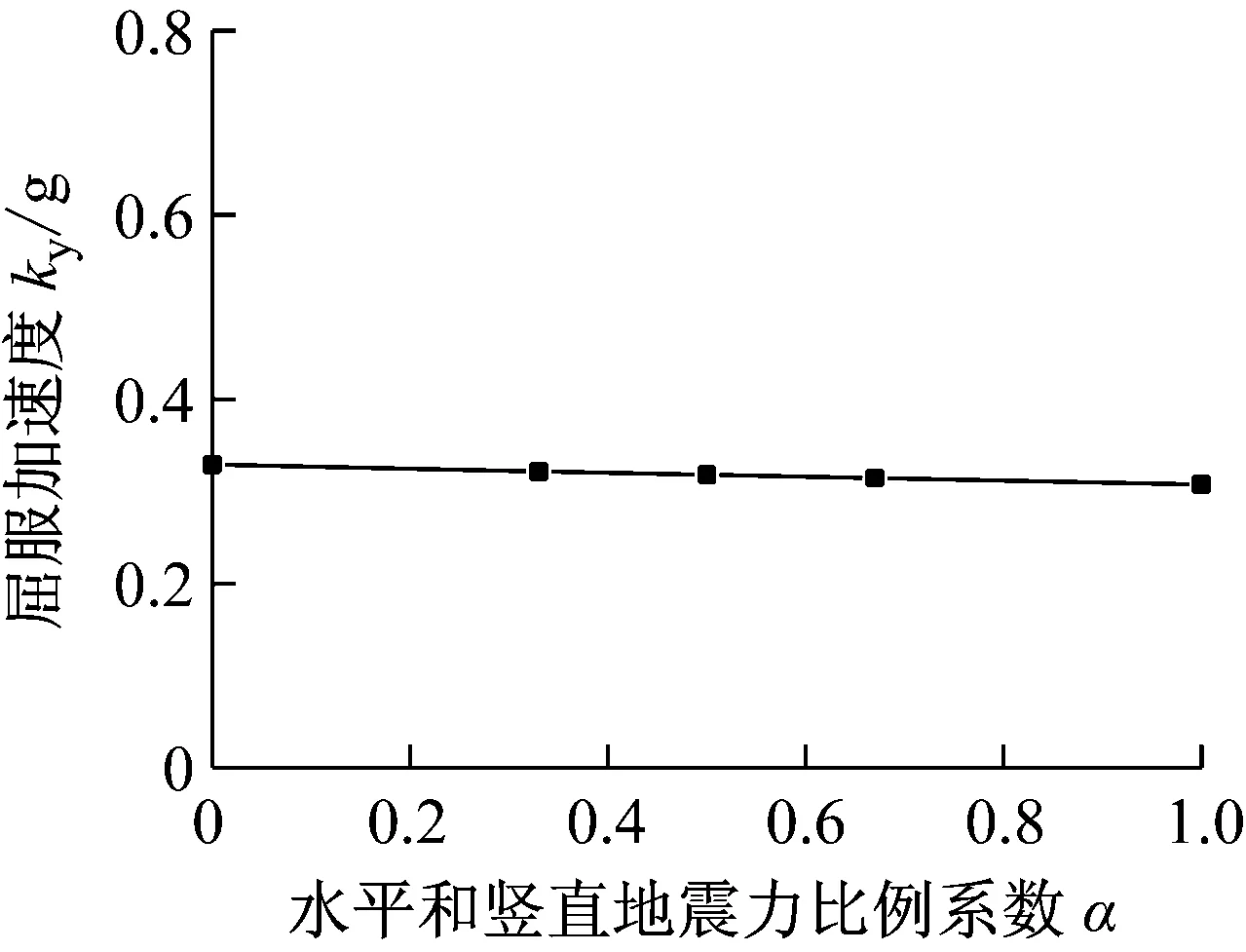
图10 水平屈服加速度系数随水平和竖向地震力比例系数的变化规律Fig.10 Change law of the horizontal yield acceleration coefficient with the coefficient of horizontal and vertical seismic force

4 结 论

基于极限分析上限定理和拟静力法，推导了地震作用下含隧道边坡的水平屈服加速度系数计算公式，并对影响因素进行敏感性和影响程度分析，主要结论如下：

(1)建立了含隧道边坡的对数螺旋线破坏机构，通过对外力做功功率和内部能量耗散功率的计算，得到了含隧道边坡的水平屈服加速度系数上限解。该上限解考虑了隧道位置、隧道埋深、支护结构抗力、地震惯性力系数、岩体的黏聚力和强度折减系数等因素。根据本文提供的极限分析方法，可进一步建立临界高度上限解和支护最小抗力上限解，综合分析边坡的稳定性。

(2)含隧道边坡水平屈服加速度系数影响因素的敏感性由大到小依次为：边坡高度H、岩土体的强度折减系数Fs、坡角β、黏聚力c、隧道距坡脚的距离d1、隧道半径R、水平和竖向地震力比例系数a。

(3)含隧道边坡的水平屈服加速度系数随着边坡高度H、坡角β、岩土体的强度折减系数Fs、隧道距坡脚的距离d1和地震力比例系数a的增大而减小，随着黏聚力c和隧道半径R的增大而增大。其中，边坡高度H，坡脚β、岩土体的强度折减系数Fs对水平屈服加速度系数的影响较大，而黏聚力c、隧道距坡脚的距离d1、隧道半径R，水平和竖向地震力比例系数a的影响较小。

(4)本文含隧道边坡极限分析方法的思想可行，结果准确，但仍存在一些不足。本文假设对数螺旋破坏面通过坡脚，并穿过隧道，当坡脚很小或对数螺旋面不穿过隧道时，此类假设并不合适。在计算隧道围岩压力时并未考虑偏压的影响，在一定程度上影响计算结果。因此，要得到一种完善且简便的计算方法，还需要进行深入的研究。