践行数学抽象,发现数学之美,体会数学之妙
2019-05-25华东师范大学第一附属中学孟庆媛
☉华东师范大学第一附属中学 孟庆媛
数学在本质上研究的是抽象的东西,数学的发展所依赖的最重要的基本思想也就是抽象,只有通过抽象才能得到抽象的东西.抽象是数学的一个长处,是数学的一个优点,是数学的一个武器.抽象是数学的一个非常突出的特点.笔者在实践教学中发现有一部分同学对抽象是反感的;有同学因数学的抽象性而感觉数学枯燥、难学.其实,这里面是有一些误解的,没有抽象,就没有数学.
例如1这样一个自然数,是经过人类多少万年抽象出来的,在客观世界里可能有1条鱼,1个果子,1块石头,1个人,但是没有1.1是从众多的客观事物中抽象出来的,经过多年以后再抽象成自然数.
数学家用抽象的方法对事物进行研究,去掉感性的东西诸如轻重、软硬、冷热,剩下的只有数量和关系,而各种规定都是针对数量和关系而制定的.有时研究位置之间的关系,有时研究可通约性,有时研究各种比例……对于数学研究而言,线、角或者其他的量的定义,不是作为存在而是作为关系.
学会数学“抽象”是一种基本的数学素养,我们应该喜爱“抽象”,并学会“抽象”的手段.
一、哥尼斯堡七桥问题,践行数学抽象
(一)问题描述
本文以大家熟悉的“哥尼斯堡七桥”问题来作为一个载体,实践数学抽象.
哥尼斯堡是欧洲一个美丽的城市,一条河流流经这个美丽的城市.河里面有两个岛,连接岸和岛、岛和岛共有七座桥,人们晚饭后沿着河岸散步,可以经过桥走到岛上去,或者经过桥走到对岸.
有一天,有一个人就想出一个游戏来,看看谁能够不重复的走遍这七座桥.不重复的走遍这七座桥,包含两个意思,第一是要把这七座桥都走遍了,第二是不能重复的走这七座桥,每座桥都只能走一遍.几天实践下来,没有一个人能找到这样的一条路线.不是少走了一座桥,就是某座桥走了两遍.

图1
这是为什么呢?
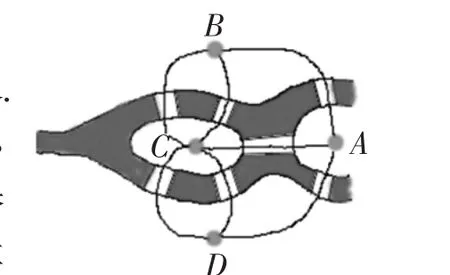
图2
(二)欧拉的三步抽象
1.第一步抽象是地图的抽象这个问题和岛的形状、大小没有关系,和这个岸的形状、桥的长短、直弯也没有关系,重要的是岸、桥、岛的相对位置关系.把岸和岛抽象成点,把这七座桥分别抽象成七条线.
第一步抽象是对地图的抽象,把地图抽象成点线图,把岛和岸都抽象成点,把桥抽象成线,这既简化了问题的条件,又突出了问题的本质.
2.第二步抽象是对问题的抽象.
不重复地走遍七座桥,欧拉把它抽象成要用一笔画出这个点线图来.既不能少画一条线,也不能重复地画一条线,这是对问题的抽象.
第二步抽象明确了问题的本质,给出了问题的表述.
3.第三步抽象是把问题转化为数学方式的叙述.
“找到一个连通的点线图可以一笔画出的充分必要条件,并且对可以用一笔画出的图形给出一笔画的方法”.
第三步抽象便于我们数学方式的理性思维.
从欧拉的三步抽象的过程中可以看到数学抽象的作用和威力.
(三)三个层次解决问题
1.第一层,把图形上的点分成两类.
通过考虑点周围的线是奇数还是偶数,把点分成这样两类:点周围线的条数是偶数的点叫偶结点,点周围线的条数是奇数的点叫奇结点.
2.第二层,探索偶结点多一些好,还是奇结点多一些好?
通过对众多图形的分析,发现要用一笔画成功,在每个点都得进去和出来,那么至少需要两条线,应该是偶结点多一些好,奇结点少一些好.
3.第三层,探索奇结点少到几个才能一笔画出呢?
点线图上的点是不公平的,可以分为两类点:第一类是起点和终点;第二类是中途经过的点.起点会有一条线只画出去而不进来,终点会有一条线只到达.显然,起点和终点都是奇结点,中途经过的点不可能是奇结点.
如果是零个奇结点,那么可以以任何一个点为起点,以任何一个点为终点,都能一笔画出;数学上可以证明点线图里的奇结点不会是一个;如果是两个奇结点,可以以其中一个为起点,另外一个为终点,就能一笔画出.
综上所述,得到“连通的点线图能够一笔画出的充分必要条件是奇结点的个数不多于两个(0个或2个)”的结论.
由于文章篇幅所限,另一方面的证明就在此省略了,因此我们可以得到:
连通的点线图能够一笔画的充分必要条件是奇结点的个数不多于两个(0个或2个).
(四)用结论解决哥尼斯堡七桥问题
反观七桥问题,在七桥问题的点线图里,有四个奇结点,不符合充分必要条件.这个点线图是不可能一笔画出的,难怪那么多人想尝试不重复地走遍这七座桥,最后都失败了.
数学道理就在此处.
二、数学抽象思想在中学数学证明中的实践
(一)问题描述
本文选取了某地区高三二模考试的第21题进行分析:

(二)问题分析
(1)第一问属于基础题目,解不等式便可解决.
(2)根据函数单调性的定义,通过作差比较,分类讨论,即可使得问题得到解决.
(3)证明题本来就是学生学习的难点,再加上纯粹的数学证明的抽象性等原因,使得学生对于证明题会出现无法下手、逻辑不清等困难.学生对于抽象的问题总是想一步到位找到解决办法,但是在平时的学习中,学生又缺乏分解问题的能力,即分步解决问题的逻辑思维和能力.对于这种抽象的题目,很多学生会选择放弃,这十分可惜.第三问确实有一定的难度,对于充分性,需要学生准确把握题干当中所提供的数据信息,根据零点存在定理准确地找到零点的范围;必要性的证明则利用了第二问的单调性结论,借助于g(x)的性质加以解决.总之,第三问的解决需要对抽象的数学证明加以分解,并通过敏锐的观察力,结合题目去加以分析论证.
(三)问题解决


三、数学抽象思想在中学数学应用中的实践
(一)问题描述
地震和风雨雷电一样,都是一种自然现象.强烈的地震,会引起地面强烈的振动,直接和间接地造成破坏.直接破坏如:由于地面强烈振动引起的地面断裂、变形、冒水、喷砂和建筑物损坏、倒塌以及对人畜造成的伤亡和财产损失等等.20世纪全球每年有记录的地震约500万次,平均每年7.0级以上的强震约13次,其中15%发生在大陆.
我国是个多地震国家,地震活跃区的居民一般都有切身体验,甚至是出生入死的亲历险境.加强对地震情况的研究和预防,与国民生活有着紧密的关系.
已知某省有A、B、C三个地震监控站,A在B的正东,相距6千米;C在B的北偏西30°方向,相距4千米.记地震中心为P.某一时刻A测到P传来的地震波,由于B、C两地比A距P远,因此一分钟后B、C监控中心才同时接收到这一地震波,已知地震波的传播速度为4千米/分.(说明:点P,A,B,C位于同一平面内)
(1)建立适当的坐标系,求地震监控站A到震中P的距离;
(2)若地震波从P点的正下方Q点处发出,则A、B收到地震波的时间差变大还是变小,并说明你的判断理由?
(二)问题解决

图3
(1)以AB的中点为原点,如图3建立直角坐标系,由题意可知,B(-3,0),A(3,0),设点P的坐标为P(x,y),因为 |PB|=|PC|,所以点P位于BC的中垂线上.所
因为|PB|-|PA|=4,所以点P位于以A、B为焦点,焦距为6的双曲线的右半支上.

四、数学文化的培养
欧拉对哥尼斯堡七桥问题的成果,最终在彼得堡科学院上发表,这篇论文是具有历史意义的一篇论文,它开创了图论的先河,其实也开创了拓扑学的先河.
数学的抽象性使得一部分学生很头疼,当然也使得很多学生因为数学的抽象美而深深地爱上了数学.不管是数学证明问题还是具体的应用题目,只要学会数学抽象的手段,对问题加以分解,步步攻克,都会柳暗花明,得到新的成果.
数学家的创新思维是值得我们学习和体会的,在中学教学和学习过程中,师生无时无刻不在实践数学抽象,通过本文希望让大家体会到抽象是数学的武器,是数学的优势.我们由此应该喜爱抽象并且学会抽象的手段,体会数学精神,学会数学思维,掌握数学方法,使用数学语言,理解数学思想,提高数学素养.
