构造函数在导数中的应用

☉新疆实验中学 郑显辉

构造函数是求解导数问题的基本方法，如何根据初等函数的导数公式和导数的基本运算法则来合理的构造出辅助函数，从而借助函数的性质来解决抽象函数的导数问题，下面举例说明.

类型一 f（x）+xf′（x）构造函数F（x）=xf（x）

例1（2018甘肃兰州一诊）已知函数y=f（x）是定义在R上的偶函数，且当x＞0时，不等式f（x）+x·f′（x）＜0 恒 成立 ，若 a=30.2·f（30.2），b=（logπ2）·f（logπ2），c=a，b，c之间的大小关系为（ ）.

解：构造函数g（x）=xf（x），则g′（x）=f（x）+xf′（x）.因为当x＞0时，不等式f（x）+x·f′（x）＜0恒成立，所以当x＞0时，g′（x）＜0.所以g（x）在（0，+∞）上单调递减.又因为函数y=f（x）是定义在R上的偶函数，所以函数g（x）=xf（x）为R上的奇函数，且在R上单调递减.因为1＜30.2＜2，0＜logπ2＜1，所以-2＜logπ2＜30.2.所以c＞b＞a.故选C.

变式nf（x）+xf′（x）构造函数F（x）=xnf（x）

F（x）=xnf（x），F′（x）=nxn-1f（x）+xnf′（x）=xn-1［nf（x）+xf ′（x）］.

类型二 xf′（x）-f（x）构造函数F（x）=

例2 （2015全国新课标Ⅱ卷理12）设函数f′（x）是奇函数f（x）（x∈R）的导函数，f（-1）=0，当x＞0时，xf′（x）-f（x）＜0，则使得f（x）＞0成立的x的取值范围是（）.

A.（-∞，-1）∪（0，1）B.（-1，0）∪（1，+∞）

C.（-∞，-1）∪（-1，0）D.（0，1）∪（1，+∞）

类型三 f′（x）+f（x）构造函数F（x）=f（x）ex

例3设（fx）是R上的可导函数，且f（′x）≥-（fx），，则（f1）的值为______.

解：由f′（x）≥-f（x）得f′（x）+f（x）≥0，所以exf′（x）+exf（x）≥0，即［exf（x）］′≥0.

设函数F（x）=exf（x），则此时有1=F（2）≥F（0）=1，

变式f′（x）+nf（x）构造函数F（x）=enxf（x），

F（x）=enxf（x），F′（x）=f′（x）enx+nenxf（x）=enx［f′（x）+nf（x）］.

类型四 f′（x）-f（x）构造函数F（x）=

例4 （2017·南昌市三模）已知函数f′（x）是函数（fx）的导函数对任意实数x都有（fx）-f（′x）＞0，则不等式（fx）＜ex-2的解集为（ ）.

A（.-∞，e）B（.1，+∞）C（.1，e）D（.e，+∞）

因为对任意实数x都有（fx）-f′（x）＞0，所以g（′x）＜0，即g（x）为R上的减函数，即g（x）＜g（1）.因为g（x）为R上的减函数，所以x＞1.所以不等式（fx）＜ex-2的解集为（1，+∞）.故选B.

类型五 f′（x）sinx+f（x）cosx构造函数F（x）=f（x）sinx

F（x）=f（x）sinx，则F ′（x）=f′（x）sinx+f（x）cosx

例5（2018届高三福建省德化永安漳平三校联考）定义在上的函数（fx），f（′x）是它的导函数，且恒有cosx（fx）+f（′x）sinx＞0成立，则（ ）.

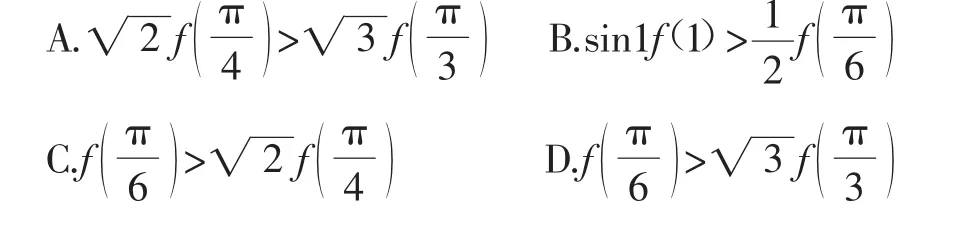
类型六 f′（x）sinx-f （x）cosx构造函数F（x）

例6定义在上的函数（fx），f（′x）是它的导函数，且恒有（fx）＞f（′x）tanx成立，则（ ）.

类型七 f′（x）cosx-f（x）sinx构造函数F（x）=f（x）cosx

F（x）=f（x）cosx，则F ′（x）=f′（x）cosx-f（x）sinx

例7设函数f（′x）是定义在（0，2π）上的函数（fx）的导函数，f（x）=f（2π-x）.当0＜x＜π时，f（x）sinx-f′（x）cosx＜0，，则a，b，c之间的大小关系为（ ）.

A.a＜b＜c B.b＜c＜a C.c＜b＜a D.c＜a＜b

解：令g（x）=（fx）cosx，则g′（x）=f（′x）cosx-（fx）sinx＞0.所以函数g（x）在（0，π）上单调递增.因为（fx）=（f2πx），所以g（x）=g（2π-x），即g（x）的图像关于x=π对称.所所以a＜b＜c.故选A.

类型八 f′（x）cosx+f（x）sinx构造函数F（x）=