给定四边的凸四边形面积范围的探究

☉广东省惠州市实验中学 刘剑锋

2017年江苏大联考给出了下面一道试题（改编）：平面凸四边形ABCD中，AB=2，BC=4，CD=5，DA=3，求该四边形面积的最大值.

此题简洁明了，趣味深刻.本文想通过对四边形面积的最大值的求解，进一步探究四边形面积的取值范围，最终将求四边形面积的取值范围的结论推广至一般情形.

一、求解四边形面积的最大值

这里给出两种求解方法：

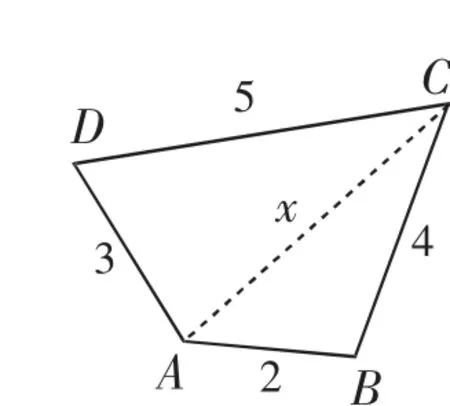
图1

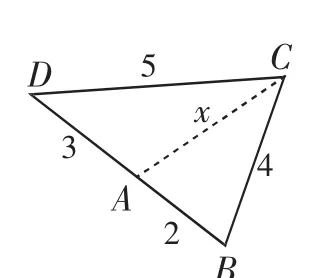
图2

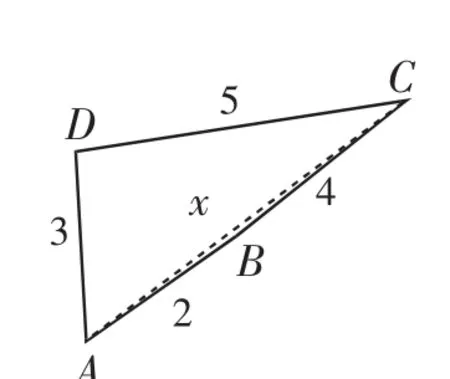
图3

解法一：如图1，连接AC，设AC=x.结合图2、图3，，且由海伦公式得四边形ABCD的面积：

解法二：由余弦定理得：

AC2=AB2+BC2-2AB·BCcosB=AD2+DC2-2AD·DCcosD，

即22+42-2×2×4cosB=32+52-2×3×5cosD，

所以15cosD-8cosB=7.①

所以15sinD+8sinB=2S.②

①2+②2得：152+82-24cos（B+D）=72+（2S）2，

即S2=60-60cos（B+D）.

注意到∠D增大，则AC增大，从而∠B也随之增大.随着∠D的减小，B、D、A趋于共线时（如图2），∠B+∠D趋于π-arccos随着∠D的增加，A、B、C趋于共线时（如图3），可见∠B+∠D的取值范围为所以当且仅当∠B+∠D=π时，S2取得最大值120，即∠B+∠D=π，四边形ABCD内接于圆时，此时面积S取得最大值为

二、探究凸四边形ABCD面积的取值范围

在上述解法二中，令∠B+∠D=α，

则S2=f（α）=60-60cosα，且 α ∈

三、给定四边的凸四边形的面积范围

如图4，在平面凸四边形ABCD中，AB=a，BC=b，CD=c，DA=d，不失一般性，不妨a≥b，a≥c，a≥d，b≥d，即AB不比其他任何边短，与AB相邻的边BC不短于AD.要构成平面凸四边形，必有a＜b+c+d.

图4

连接AC，由余弦定理得：

AC2=AB2+BC2-2AB·BCcosB=AD2+DC2-2AD·DCcosD，

即a2+b2-2×a×bcosB=c2+d2-2×c×dcosD，

所以2abcosB-2cdcosD=a2+b2-c2-d2.①

所以2absinB+2cdsinD=4S.②

①2+②2得：4a2b2+4c2d2-8abcdcos（B+D）=（a2+b2-c2-d2）2+（4S）2，

即（4S）2=4a2b2+4c2d2-（a2+b2-c2-d2）2-8abcdcos（B+D）.

图5

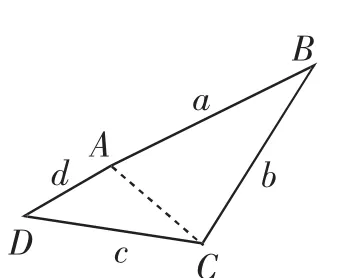
图7

图6

注意到∠B增大，则AC增大，从而∠D也增大.随着∠B的增加，A、D、C趋于共线（如图5），从而∠B+∠D趋于π+arccos当a+d≥b+c时，随着∠B的减小，B、C、D三点趋于共线（如图6），从而∠B+∠D趋于π-arcco；当a+d＜b+c时，随着∠B的减小，B、A、D三点趋于共线（如图7），从而∠B+∠D趋于

所以当a+d≥b+c时，∠B+∠D的取值范围为

当a+d＜b+c时，∠B+∠D的取值范围为

因此，无论a+d≥b+c，或a+d＜b+c，∠B+∠D都可取得π，从而（4S）2取得最大值M=4a2b2+4c2d2-（a2+b2-c2-d2）2+8abcd=（a+b+c-d）（b+c+d-a）（c+d+a-b）（d+a+b-c）.

当a+d≥b+c时，（4S）2关于∠B+∠D

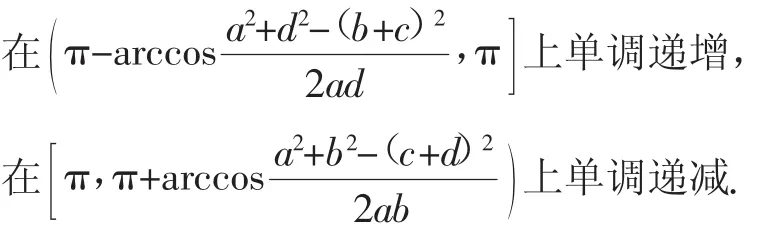
综上可得如下一般性结论：

任意给定凸四边形的四边，当最长的边及与其相邻的较长的边夹角变小，凸四边形趋于一个三角形时，凸四边形的面积趋于其下限；凸四边形变为内接于圆时，其面积取得最大值.

实战：凸四边形的四边依次为3，5，7，11，求其面积的取值范围.

根据上述一般性结论，当长为7，11的两边夹角变小，凸四边形趋于以3，11，7+5为边的三角形时，凸四边形面积趋于该三角形的面积为；当凸四边形变为内接于圆时，其面积取得最大为.因此该凸四边形面积的取值范围为