增长型时间序列组合模型设计及医院费用预测实证比较*
2019-05-24李望晨张利平
李望晨 井 淇 姚 琳 张利平△
1.潍坊医学院“健康山东”重大社会风险预测与治理协同创新中心(261053) 2.潍坊医学院经济管理学院
时间序列分析常见于经济、管理、卫生、医疗领域指标预测问题,它以预测事物本身随时间变化数据规律来提取信息,以数学方法拟合历史数据并外推预测未来。拟合预测精度最受应用工作者关注[1]。时序资料表现为随时间变化呈平滑递增趋势特点,无明显扰动、周期性或季节性,曲线拟合法、ARIMA法为常见方法,算法原理不同但拟合外推性能较好[2]。组合预测模型设计目的是集结每种方法优点,提高拟合性能及外推预测效果。本文针对此类资料特点探索几种组合建模方法,通过案例比较和验证组合建模方法对医疗费用预测的意义。
单项方法
经济或卫生领域某些指标变化规律往往符合平稳增长特点,如住院人次、卫生费用[3]、门诊人次[4]、卫生投入、医院效益等,此类资料组合预测模型设计有相似通用意义。
设某医院费用某指标时序资料,t1~t13为历史数据,t14为待预测数据,见表1。

表1 某医院费用某指标时序资料(万元)
针对时序资料先以单个方法建立模型,再考虑从多个视角建立组合模型,分析组合设计特点并比较拟合外推性能,为类似增长趋势变化特点的预测问题提供参考。
1.曲线拟合法
应用前提是历史数据随时间呈较平滑曲线变化特点,在自身数据与时间t之间建立函数关系yt=f(t),并用曲线(如直线、抛物线、指数曲线、逻辑曲线等类型)描述关系,有时会有多种类型均适用,可在继续计算增长特征以后选择最优者,即用差分法寻求增长特征,精确描述序列数据变化特点并与曲线模型理论增长性质比较。
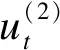
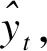
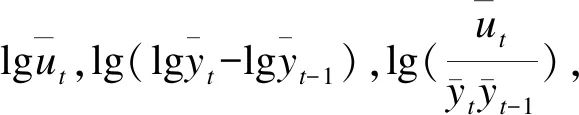
2.ARIMA法

ARIMA法用于平稳序列分析,对递增趋势数据须作低阶差分,差分过度也会丧失信息。序列数据须先作纯随机检验,检验是否有建模分析意义。首先确定模型结构和阶数,可以低阶试取或自动寻优,接下来用条件最小二乘法识别参数以检验参数显著性。建模以后须检验信息是否提取充分,对残差序列作纯随机检验。ARIMA法建立历史序列和残差序列线性关系,却不易直观解读数据随时间的真实变动规律。
3.独立验证
该时序资料有增长趋势,作为非平稳序列须作二阶差分,通过纯随机检验,由低阶到高阶逐步试取模型结构。(1+0.20501B+0.4373B2)(1-B)2xt=εt为最终识别模型。残差序列作纯随机检验,延迟6阶P=0.4838>0.05,自相关系数为0.101,0.108,0.322,0.174,0.176,0.030;模型对原始数据信息提取已经较充分,外推预测值25002.71,95%置信区间[23345.98,26659.43]。对历史数据拟合4731.68,5367.35,6230.68,7273,9236.36,10854.88,13728.62,14626.73,19121.26,23312.13。两类方法对历史数据拟合并计算残差序列。
由此分别计算平均相对误差绝对值2.52%、5.37%。分别演示拟合效果,见图1~2。
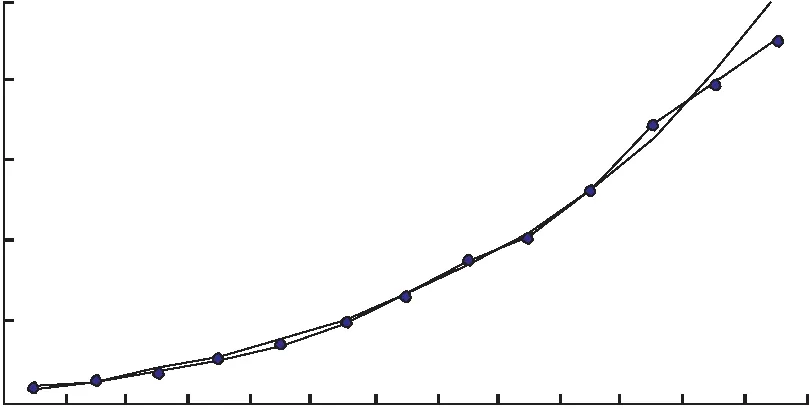
图1 修正指数曲线拟合外推效果
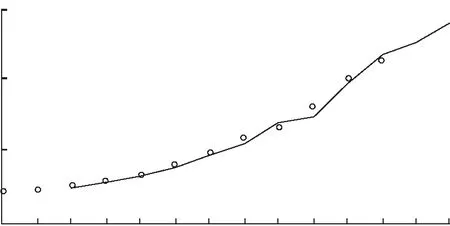
图2 ARIMA法拟合外推效果
曲线拟合法适于趋势增长数据平滑修匀,历史数据拟合好,近期增长趋势有类似“拐点”特点,若以指数递增外推未来而引起“乐观”预测;经差分后以ARIMA法提取序列短期相关性,ARIMA法反映历史数据长期变化,拟合效果也很好,但对后期快速增长趋势难以适应,会引起“悲观”预测。于是引入多种组合设计思路折中分析并检验拟合外推效果。
组合方法
上述方法数学理论不同、信息应用有差异,组合设计拟合性能或外推精度一般会更优,线性加权思路常见[5],即以多种思路将历史拟合值与原始值接近为依据计算权重,将代表方法加权合成组合模型,进一步提高拟合及预测精度。
1.SSE倒数法

两类方法建模拟合后得残差序列e11,e12,…,e1t与e21,e22,…,e2t。然后计算Q1=143794.15,Q2=571579.14。取倒数并归一化为权重w1=0.799,w2=0.201。两类方法预测值加权组合:0.799×28005+0.201×25002=27401。
2.关联分析法

两类方法拟合为历史数据,计算与真值序列灰色关联系数:0.794,0.672,0.573,0.851,1,0.520,0.637,0.942,0.346,0.420;1,0.917,0.896,0.648,0.876,0.579,0.756,0.410,0.525,0.669。分别合成灰色关联度γ1=0.6756,γ2=0.75275。计算权重w1=0.4815,w2=0.5185。两类方法预测值进行加权组合0.4815×28005+0.5185×25002=26447。
3.相关分析法
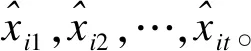
两类方法拟合历史数据,分别计算与原始序列相关系数:r1=0.998,r2=0.994。计算权重w1=0.5010,w2=0.4990。两类方法预测值加权组合:0.5010×28005+0.4990×25002= 26502。
4.待定值法
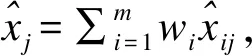
5.平均法
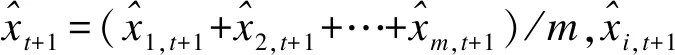
6.结果列举
不同方法平均相对误差ME和外推预测值F,见表2。

表2 不同方法实施方法的结果比较
讨论
卫生领域许多指标数据随时间变化呈稳定递增特点,无周期性、季节性、强干扰性和波折性,曲线拟合法和ARIMA法为两类时间序列分析方法。曲线拟合法中有许多类型,由数据资料平稳递增特点分析,根据曲线理论性质与数据变化特点匹配,以增长特征法选择模型。
通过文中增长型医院费用案例探索性设计多类组合模型并对数据集选择、模型特点和结果分析进行解读。由表1分析,实例资料数据有明显指数曲线变化特点,曲线拟合法拟合较好,外推时会对增长趋势惯性延续反映;ARIMA反映早期平缓变化以及长期变化特点,低估中后期增长趋势[6]。根据两类建模思想进行组合分析,确保拟合性能条件下改善外推精度。将多种组合方式给予流程简述和案例演示,兼顾不同方法原理以及拟合性能,缓解对历史资料过拟合,“中庸折合”后提高外推预测精度。如果此规律惯性延续,则兼顾多类组合模型优点,而将其预测值均数26491折中为参考值,多类组合方法有综合设计意义。
SSE倒数法、关联分析法、相关分析法、待定值法、平均法从理论可解释性、操作可行性角度给出单项方法组合方法,设计过程中单项预测方法作用以较大权重来体现,如SSE倒数法是从残差平方和最小角度、关联分析法是从拟合序列与真值序列灰色关联系数最大角度、相关分析法是从拟合序列与真值序列相关系数最大角度、待定值法是从最小化组合模型残差优化分配系数角度、平均值法是从假设各单项方法等量体现权重角度。拟合效果或相对平均误差均不错,而SSE倒数法对于历史数据拟合效果更佳;所有模型共同使用的外推预测结果折中分析更有均衡或综合的实际参考价值。
经分析,曲线拟合法拟合性能好,外推时过度反映增长趋势而高估预测值;ARIMA法拟合非最好,外推时反应早期平缓规律而低估预测值。近期不可控变动因素引起趋势增长不平稳,趋势变化“偏离”历史惯性,ARIMA法以历史资料为依据修正。组合建模方式均衡历史规律拟合效果,缓解过度拟合或拟合不足问题,在保证拟合效果的前提下,折中互补并改善外推预测效果。倘若时间序列不仅有递增发展趋势,还有周期性或季节性变化特点,当然亦可由季节指数或季节差分法来提取周期性信息,才能对于消除周期性信息以后的增长型序列参照上述组合方法拟合建模,充分挖掘序列复杂信息并提高预测精度。
时间序列方法多用于历史拟合以后短期外推应用,历史数据体现了过去或近期事物发展规律,样本量选取多少也不能一概而论,不同时期历史数据反映不同时期延续变化规律信息,历史信息过度拟合反而降低近期外推性能,将其过度纳入反而污染了近期信息而导致预测效果变差。数据资料选择要根据方法原理理论、实际数据特点、信息复杂程度和专业行业经验来综合优选设计,从而科学辅助管理决策工作。
