随机缩减法在拒绝型O’Brien & Fleming成组序贯设计中的应用研究*

南方医科大学公共卫生学院生物统计学系(510515) 刘伟杰 谭旭辉

【提 要】 目的 比较随机缩减法中条件功效和不同先验分布下的预测功效两类指标的优劣。方法 以试验组和对照组的两样本均数比较的统计优效性检验为分析目的,在拒绝型O’Brien & Fleming(OBF法)成组序贯设计的条件下,通过设定不同SCP的拒绝阈值γ,在每个期中分析阶段计算CP及不同先验下的PP,并计算各指标相应的Ⅰ类错误、检验功效Power、平均样本量以及平均阶段数。结果 当SCP终止条件为γ=0.80,无信息先验PP的Ⅰ类错误能稳定在0.05处左右,而CP和enthusiastic先验PP的Ⅰ类错误则出现明显膨胀;当SCP终止阈值为0.85和0.90,能明显抑制CP和不同先验下的PP的Ⅰ类错误的膨胀;当五阶段OBF功效设定在90%及SCP终止阈值为0.80的条件下,CP、无信息先验PP以及enthusiastic先验PP功效分别为87.6%、84%和86.5%。结论 在期中分析次数较多的OBF成组序贯设计条件下,无信息先验PP效果优于CP;在阳性研究中,SCP能大幅减少成组序贯试验所需的期望样本量和期望阶段数。随着SCP终止阈值的增大以及期中分析次数的减少,CP和不同先验PP的功效均会出现明显的下降,而CP和不同先验PP的Ⅰ类错误的膨胀则会被抑制。随机缩减法相关指标对于临床试验有效性监测具有较高的参考价值。

临床试验数据的安全性和有效性的期中监测成为了现代临床试验重要组成部分,成组序贯设计因其期中分析的灵活性成为药物临床试验设计方法的较好选择。为了在试验过程中,能够对未来的结局进行预测,由Lan,Simon & Halperin[1]基于序贯设计的思想提出的随机缩减法(stochastic curtailment procedure,SCP)则是可以有效降低样本量的试验数据监测方法。此外,在Ⅲ期临床试验有效性评价中,成组序贯设计通常会选择O’Brien & Fleming(下称OBF法)法[2]。因此,在OBF法成组序贯设计条件下结合随机缩减法的各个指标,能否进一步提高试验效率亟待明确。故本文主要以OBF法作为经典期中分析方法,在参数θ的先验分布取“客观性”较强的几种先验分布条件下,对随机缩减法的条件功效(conditional power,CP)和预测功效(predictive power,PP)进行比较和评估,为该方法在成组序贯设计中的应用提供理论参考。

方法与原理

1.成组序贯设计

成组序贯设计(group sequential design)是一种在试验正式结束前,能提供多次期中分析的设计。在该设计中,因其能较早的终止试验,从而明显减少试验所需样本量以及时间。从设计角度来说,成组序贯设计是将整个试验划分成K个阶段,每个阶段内都有一定量的受试者加入,当第k个阶段(k=1,2,…,K)结束后,将之前各个阶段试验结果累积起来进行一次分析。对于拒绝型的成组序贯设计,如果拒绝H0则试验结束,否则继续下一阶段试验。在最终试验阶段,其结果不是接受H0,就是拒绝H0[2]。

期中分析(interim analysis)[3-4]是根据事先制订的分析计划,对累积数据进行分析并比较处理组间的有效性和安全性。期中分析可提早终止试验并缩短试验周期,同时可保证患者以较少的花费得到最佳的治疗。由于该过程实际上是对已累积数据进行重复性检验,为防止Ⅰ类错误膨胀,成组序贯设计在各阶段校正检验水准,各阶段的Ⅰ类错误被称为名义显著性水准(nominal significance level)[5]。

2.随机缩减法

在临床试验中,如果试验在某阶段累积的信息可保证在整个试验完成时有较大可能性得到拒绝或接受零假设的结论,那么试验即可在此阶段结束。基于以上规则,由Lan[1]提出的随机缩减法(SCP),可在试验过程中的任意一个阶段,通过计算SCP的相关指标来判断试验是否可以提前终止。SCP指标有如下两类[6]:

(1)条件功效(CP),即以当前所纳入样本提供的信息推测最终阶段拒绝原假设的概率:

CPk(θ)=P(RejectH0|θ,accumulated data)

(1)

对于每一阶段k=1,…,K-1,在Zk条件下的最后阶段ZK的条件分布为:

那么第k阶段的CP为

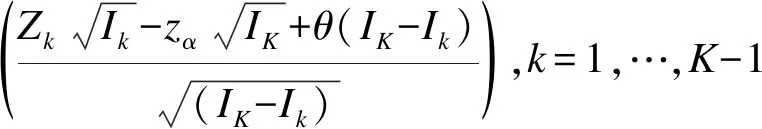
(2)

CP的计算取决于未知的真实效应差别θ,一般取现阶段的最大似然估计值θMLE[6]。

(2)预测功效(PP),即依据θ的先验信息,并结合样本似然函数,以后验分布作为权重对θ进行积分[7-8]。

(3)

PP相对于CP,有效地避免了直接选择参数θ估计值进行计算,并以θ的后验分布作为权重,计算加权平均的条件功效。该方法在计算中用θ的后验分布反映了对θ的不确定性,从而需要事先指定θ的先验分布。

P(θ|accumulated data)～

(4)

则根据公式(3)、(4),第k阶段的预测功效为

PPk=

(5)

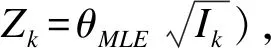
本研究中所采用的几种“客观性”较强的先验分布如下[9-11]:

Non-informative先验(无信息先验):若假设临床试验开始前我们缺少试验相关历史信息。在这种情况下,先验参数会在一个区间内取值没有任何倾向;

Enthusiastic先验:当临床试验结局支持阴性结果(Negative Study)时,我们选择Enthusiastic先验来计算预测功效PP,并以此推断试验数据支持阴性结果的强度;对于正态Enthusiastic先验分布,要求其先验均值取为θalternative,取Prob{θ≤0}≤α成立时的方差;

Skeptical先验:当临床试验结局支持阳性结果(positive study)时,我们选择Skeptical先验来计算预测功效PP,并以此来判断试验是否终止。对于正态Skeptical先验分布,要求其先验均值取为0,取Prob{θ≥θalternative}≤α成立时的方差;

本文通过随机模拟,对拒绝型OBF法成组序贯设计下条件功效CP和预测功效PP作为试验监测指标的优劣性进行比较,并评估各种先验分布对PP的影响;比较不同SCP终止阈值γ对CP和PP监测效果的影响。

模拟比较

我们以两样本均数比较的成组序贯为设计框架,采用SAS 9.3随机产生每个阶段的模拟试验数据。在期中分析中,通过计算CP和PP的I类错误、检验功效Power、平均样本量(average sample number,ASN)以及平均终止阶段数(average stage,AS)等指标,综合评价CP和PP的优劣性。在模拟过程中,试验是否终止的判断是由经典OBF期中分析的结果来决定。

在模拟过程中,以优效性假设检验H0:θ=0,H1:θ>0(θA=2),单侧α=0.05,β=0.1(即Power=0.9),经典OBF法成组序贯设计阶段数K=3,4,5为设计框架;效应差值θA=2,共同标准差σ=8,试验组均值Μt=4或6,对照组均值Μc=4;SCP阈值设定为0.80、0.85以及0.90;模拟次数为1000次。具体参数如下表1所示:

表1 模拟参数设定

结果

1.两总体均数相同

在两总体均数相同条件下,按照表1的参数设置,随机缩减法的各指标的I类错误如表2。由表2的阴性模拟研究结果中可以看出,在终止条件为γ=0.80的5阶段和4阶段情况下,随机缩减法的各指标除Skeptical先验PP以外均有Ⅰ类错误膨胀的情况,尤其是指标CP的I类错误出现较明显的膨胀。另外,Skeptical先验通常用于支持阳性试验结局,因此在阴性模拟比较中I类错误较低,其实际参考意义不大。而在三个阶段中的无信息先验PP的Ⅰ类错误能稳定在0.05左右。

当终止条件设定为γ=0.85或γ=0.90,随机缩减法的各指标除CP以外均能较好控制Ⅰ类错误膨胀的情况,Ⅰ类错误随着阶段数的减少而降低,当阶段数降低到3阶段时,指标CP的Ⅰ类错误概率能控制在0.05左右。

2.两总体均数不同

在两总体均数不同条件下,按照表1的参数设置,随机缩减法的各指标的功效(Power)、平均样本量(ASN)及平均终止阶段数(AS)如表3。

由表3的结果可以看出,在终止条件γ=0.80的5阶段情况下,CP、无信息先验PP和Enthusiastic先验PP的功效Power均能保持在0.85左右,SCP各指标的平均样本量(ASN)及平均终止阶段数(AS)均比OBF法有明显的降低。在γ=0.80的各阶段情况下,随着阶段数的减少,SCP各指标的功效均会比OBF法有明显的降低。

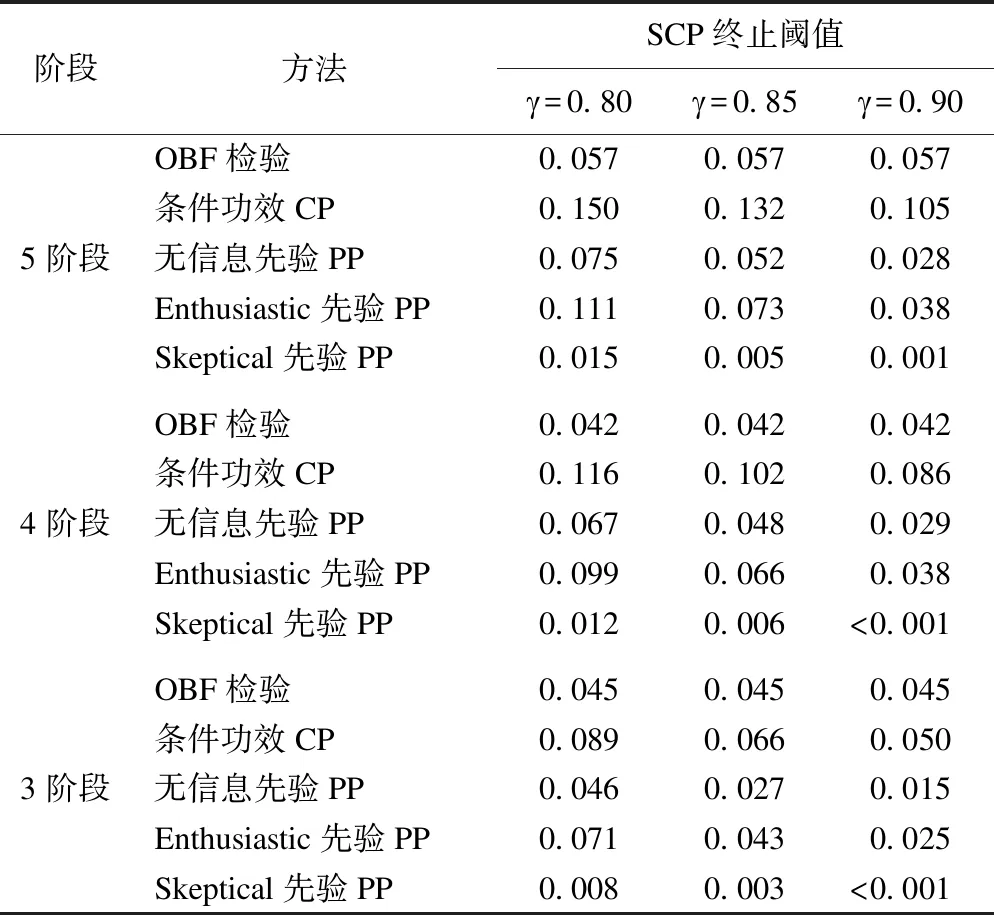
表2 两总体均数相等时I类错误

在相同阶段数的条件下,随着γ值的增大,SCP各指标的功效均会出现明显下降。此外随着阶段数的减少,SCP各指标的功效均会有明显的下降。在各阶段情况下,SCP各指标的平均样本量(ASN)及平均终止阶段数(AS)仍然比OBF法要低。

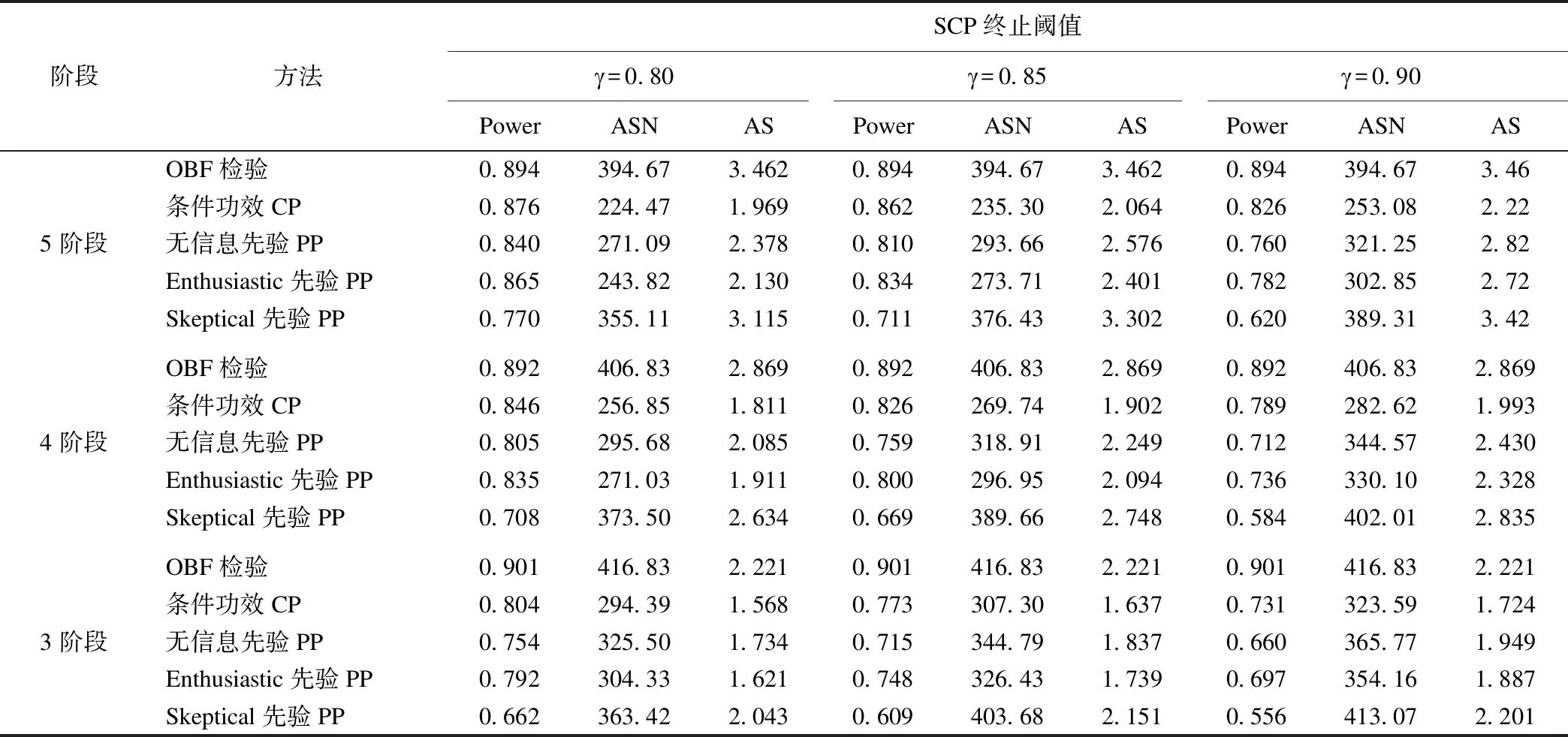
表3 两总体均数不等时功效(Power)、平均样本量(ASN)及平均终止阶段数(AS)

讨论

本文主要对随机缩减法原理进行了简单阐述,并对其在经典成组序贯设计期中分析过程中的应用效果进行了分析比较。从实际模拟效果来看,在期中分析次数较多的情况下,CP会明显增加I类错误的风险[12],而无信息先验PP和Skeptical先验PP均能较好的控制I类错误。随着期中分析次数的减少,无信息先验PP和Skeptical先验PP的I类错误控制情况依旧好于条件功效CP。因此,在阴性研究中无信息先验的PP是优于条件功效CP的。这是由于在试验的早期阶段,参数θ的最大似然估计值θMLE通常是不太稳定的,从而使条件功效CP的计算存在较大的误差,并由此导致在试验的早期阶段过多的拒绝零假设。对于无信息先验的PP,由于其计算中依赖的是θ的后验分布,所以PP的计算是比较合理和稳定的。从先验分布的选择角度来说,无信息先验也是较理想的选择。此外,随着期中分析次数的降低,每阶段所需的样本量就会相应的增加,从而使参数θ最大似然估计值趋于稳定。这种现象恰恰说了随着期中分析次数的减少,条件功效CP的I类错误膨胀情况得到明显的抑制。

在总体均数不同以及期中分析次数较多的情况下,基于CP、无信息先验PP以及Enthusiastic先验PP的功效Power均能较好的接近OBF法设定的功效,而相应的平均样本量和平均阶段数均明显的低于OBF法,尤其是CP比无信息先验PP更加节省样本量。但是,这并不能说明在阳性研究中条件功效CP是优于无信息先验PP的。这是由于CP在试验的早期阶段拒绝零假设,通过放大I类错误,从而获得了较高的功效Power以及较低的样本量。随着期中分析次数的减少,SCP各指标的功效均会出现较明显的下降,这也就意味着SCP各指标并不适用于期中分析次数较少的设计。

通过整个模拟试验,我们发现SCP阈值γ的增加或减少均会明显影响各个指标的I类错误和功效,这是由于随机缩减法的判断原理造成的。Jennison[6]的研究表明,SCP阈值γ较理想的取值是在0.8到0.9,这与我们的模拟结果是一致的。

综上所述,当在OBF法拒绝型成组序贯设计中,在期中分析次数较多的情况下,随机缩减法中的基于无信息先验的PP可作为临床试验早期决策的辅助参考指标,从而增加研究人员对未来结果预测的信心。