双向比对高精度物理时间同步方法
2019-05-24于雪晖王盾李周赵鸿娟
于雪晖,王盾,李周,赵鸿娟
航天恒星科技有限公司,北京 100194
随着现代微小卫星技术的进步,多颗物理上远距离分布的小卫星协同工作,形成一个“卫星编队”或“虚拟卫星”共同完成空间任务,成为一种迅速发展的空间系统部署方式,称为分布式卫星系统(Distributed Satellite System, DSS)。与单颗大卫星相比,分布式卫星系统具有诸多优势,例如:通过卫星协作显著提高整体性能,有效降低系统寿命周期,提高可靠性、抗毁性、和任务适应性等[1]。
时间同步和空间同步是多星系统在轨服务需要解决的最关键问题,而时间同步同时又是空间同步的基础。因此星间时间同步是多星系统的应用基础,左右系统任务完成的效能。以精确导航制导、分布式雷达系统、激光聚变技术、相位阵列天线技术、高性能原子钟比对为代表的先进信息技术领域和前沿科学领域对于高精度时间同步及其性能的评估校准要求不断提升,从原有的毫秒、微秒、亚微秒量级逐步发展到现在的纳秒。
在现阶段精确时间同步体制中,国内外实现时间同步有3种技术途径:
1) 物理调钟:能够从源头上消除时钟相隔系统中钟差对“观察数据”的污染[2-6]。Kishimoto等[5]在准天顶导航卫星上搭载时间同步设备开展星地实时物理调钟试验以地面原子时为基准保证星上钟面时物理同步,时间同步精度为2~10 ns。相似地,Glennon等[7]开展了Biarri立方星项目,依靠GPS(Global Positioning System)授时方式,在轨调整石英晶振,完成组网星座的时间同步,同步精度为20 ns。
2) 补偿修正:钟差检测补偿修正技术,仅通过数据处理的方式修复“观察数据”中的钟差污染项,而不物理调钟,是一种“软同步”方式,既可以实时实现,也可以通过事后处理的方式实现。其“实时实现”的典型应用包括文献[8-11]给出的卫星双向时间频率传递技术(Two Way Satellite Time and Frequency Transfer, TWSTFT),钟差测量精度约为1~10 ns;文献[12-13]给出的GPS实时授时技术,钟差测量精度约为20~500 ns;GPS实时共视技术,钟差测量精度约为5~20 ns。其“事后处理”实现的典型应用是[14-18]:地球重力场测量(Gravity Recovery And Climate Experiment, GRACE)、IGS(International GNSS Service)信息辅助的GPS共视法等,钟差测量精度约为0.1~1 ns。
3) 组合方式:实时物理调钟技术和钟差检测补偿修正技术的组合形式,当钟差在一定限度内,进行补偿修正;当钟差超过一定限度时,物理调钟。典型应用是BD2/GPS星载原子钟校时技术[19-21]。BD2/GPS运控中心持续监视星载原子钟与本系统时(BD2/GPS时)的差异。当钟差在一定限度内时,不物理调钟,仅仅是通过修改导航电文中的钟差修正项信息的方式将该钟差信息广播给用户做钟差补偿使用。只有当钟差超过一定限度时,才会物理调钟,但值得注意的是,每次物理调钟时BD2/GPS会暂时中断授时服务。
基于以上调研分析,目前国内外主要卫星系统的时间同步试验大多依赖于地面或GNSS(Global Navigation Satellite System),导致其在战时或其他特定条件下存在着极强的风险;双向时间频率传递技术虽然解决了系统的自主性问题,但很难从时钟源头消除钟差给其他应用主载荷带来的影响。
“物理调钟”在本地时钟驯服系统应用较为广泛,但是在远程相隔系统高精度时间同步领域中却罕见应用案例[22-25]。本文首先利用时钟比对技术获得钟差观测量,然后利用时钟比对技术输出的钟差观测量物理校调本地星载石英钟,使得两地钟差物理同步精度达到ns级。从源头上彻底抑制和消除钟差对分布式科学观测数据的污染,且具有较好的通用性,可以作为基本通用组件在卫星系统上使用,同时解决了类似BD2/GPS调钟过程中服务中断的连续性问题。
就同步精度指标而言,“补偿修正”与本文采用的“物理调钟”的内涵也是不相同的。“补偿修正方式”提出的同步精度指标实际上是时钟比对技术的钟差测量精度指标,通常是长期统计的平均结果。而“时钟物理同步技术”提出的同步精度指标则是时钟实时物理同步精度。显然,就同步精度指标获取方式而言,前者是非实时的,后者是实时的;就抑制钟差污染的应用目的而言,前者获得是需要再加工的初步数据,加工过程还会引入新的误差,而后者则是最终结果。因此,在相同的指标参数情况下,物理调钟方法实现的难度更大,代表更先进的技术水平。
物理调钟与修正模式相结合的方式当钟差超出限度范围时,需要做物理调整,此时由于主从星较大的钟面时差异,必须使用较大的调节量才能将从星频率源一次拉回到主星频率源附近,相当于外部施加了一个冲激激励,并未有逐步锁相的过程,导致频率源的不稳定振荡,在等待频率源稳定的一段时间内无法对外提供稳定准确的频标信号或授时服务。本文讨论的物理调钟方法,是一种锁相的概念,与目前物理调钟与修正模式相结合方式不同之处在于,它是一个钟差高精度测量与高精度时钟调整的逐步迭代,缓慢收敛的过程,不会带来频率源阶跃性振荡。当时钟调整稳定后,两星钟差几乎为零,时钟调节量也逐步趋近于零,此时极小的调节量不会再引起频率的不稳定振荡,将从星频率源长期锁定在主星,保证两星的频率和相位相干。
1 星间时间同步基本模型
图1为星间时间同步基本模型。整个系统由两大基本环路组成:① 主从卫星间的钟差测量环路;② 从星的时钟同步环路。钟差测量环路的输出为两星间钟差观测值,其作为时钟同步环路的输入进行时钟的调整,时钟调整的结果再反映到从星的秒脉冲(1 Pulse Per Second, 1PPS)信号,由于从星的发射信号依赖于1PPS信号,因此,时钟调整的结果进而会反映到主从星的测距结果及其钟差测量结果。二者通过如此反复闭环调整,实现最后的钟差收敛为0,即二者时间达到同步。
由星间时间同步基本模型可以分解出实现流程如下:
1) 主从星分别搭载原子钟与带压控引脚的晶体振荡器(Voltage Control X-tal Oscillator, VCXO)作为各自星上时间频率基准,产生1PPS与时间间隔计数器(Time Interval Counter, TIC)信号。
图1 星间时间同步基本模型Fig.1 Time synchronization model for inter-satellite
2) 主从星各自进行伪距测量,测距结果应消除自由空间信号传递引入的各种误差。
3) 通过电文的传递,将主星伪距观测值传递给从星。
4) 从星经过数据解调得到主星伪距观测值,再与之前缓存的从星伪距观测值进行比对,最后得到当时的两星间钟差。
5) 从星通过环路滤波器输出平滑后的钟差,经过数模转换将钟差值转换为电压模拟量,输出控制电压不断校正从星本地压控频率源的振荡频率使其与主星参考频率源的输出频率同步,并最终达到一种稳定状态。
2 基于双向测距和时间传递技术的钟差测量
采用双向测距和时间传递技术消除信道传播延时对钟差测量量的影响,其基本思想是通过差分处理去除了相等的路径传播延时。
图2为钟差测量原理图,其中M为主控卫星(Master Satellite),搭载原子钟作为系统时间基准。S为从属卫星(Slave Satellite),搭载石英晶振。tM为主星M的本地时,tS为从星S的本地时,tref为系统参考时。图中,S钟超前M钟。特别地,当S本地时等于tn时,主从卫星系统钟差为Δt(tn)。钟差测量流程如下:
步骤1主从卫星同时进行伪距观测
主从卫星约定在相同的本地时刻(如本地时=tn),同时检测接收信号的伪码相位(伪同时)。再结合接收信号电文,可以无模糊地推算出以对方本地时表示的信号发射时刻,进而计算出伪距。
(1)
式中:TS为S发射设备内部延时;τU为上行链路空间传播延时;RM为M接收设备内部延时。因此,S信号发射时刻(系统参考时)为
(2)


图2 钟差测量原理Fig.2 Principle of clock bias measurement

(3)
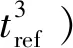
(4)

(5)

(6)

(7)
步骤2从星S缓存伪距观测值,主星M组帧发送伪距观测值。
获得伪距测量值后,从星S将伪距测量值缓存在本地数据查找表中,存储格式为
(8)
主星M将伪距测量值编制成电文通过链路传输给传输从星S,电文中相关电文子项为
(9)
tn可由电文中半秒计数器结合一些数据约定得出,而pM(tn)则直接调制在主星M的时差测量数据块中。
步骤3从星S解帧并计算钟差

(10)

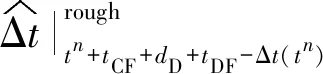
RS(tn)]=Δt(tn)- (系统钟差)
(从星S收发通道的设备零值差)
(主星M收发通道的设备零值差)
(上下行链路的空间传播延时差)
(11)
如式(11)所示,不同时刻非对等的传播路径延时误差主要包括主从卫星收发通道在不同时刻的设备零值差、上下行链路在不同时刻的空间传播延时差。
上下行链路在不同时刻的空间传播延时差主要受到卫星相对运动(不同时刻的路径长度不同)和电离层等频率扩散信道的影响(不同收发频点的路径传播延时不同)。
经过基于收发通道设备零值差标校的设备零值补偿、基于载波多普勒测速信息的卫星相对运动补偿、以及基于单向双频测距数据融合处理的电离层群延时补偿等补偿措施修正后的钟差观测量为

(12)
步骤4从星S微调本地时钟,逐步减小系统钟差Δt,使之趋近于零。
3 误差传播分析及指标分解
通过式(11)分解,可以将钟差表示为
(13)
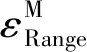
由于主从星伪距测量方式相同,不妨设主从卫星伪距观测量的1σ标准差都为σRange(二者近似相等),主从卫星收发设备内部延时差标校值的1σ标准差都为σDiffGD(二者近似相等),由卫星相对运动引入的信道多普勒频移误差的1σ标准差为σDPL,由电离层频率选择性引入的双向路径延时差的1σ标准差为σION,且设所有误差源互相独立,则可得总的星间钟差测量误差的1σ标准差为
σ钟差测量=
(14)
由于时间同步技术不仅需要进行钟差测量,还需要进行时钟调整,因此误差项还应包括时钟调整部分,即
(15)
本文以1σ为精度判据,根据误差传递模型对时间同步精度优于1 ns的应用技术指标进行3级分解(见图3),其中时间同步可分解为时间测量和时间调整两部分,进一步通过以下4种技术分别对第2节中时间测量原理分解得到的误差进行修正:载波相位平滑伪距技术(修正伪距测量误差)、双频电离层校正技术(修正电离层引入误差)、高精度零值校准技术(修正器件老化等问题引入的误差)和基于多普勒频移的相对运动补偿技术(修正相对运动引入的时延误差)。
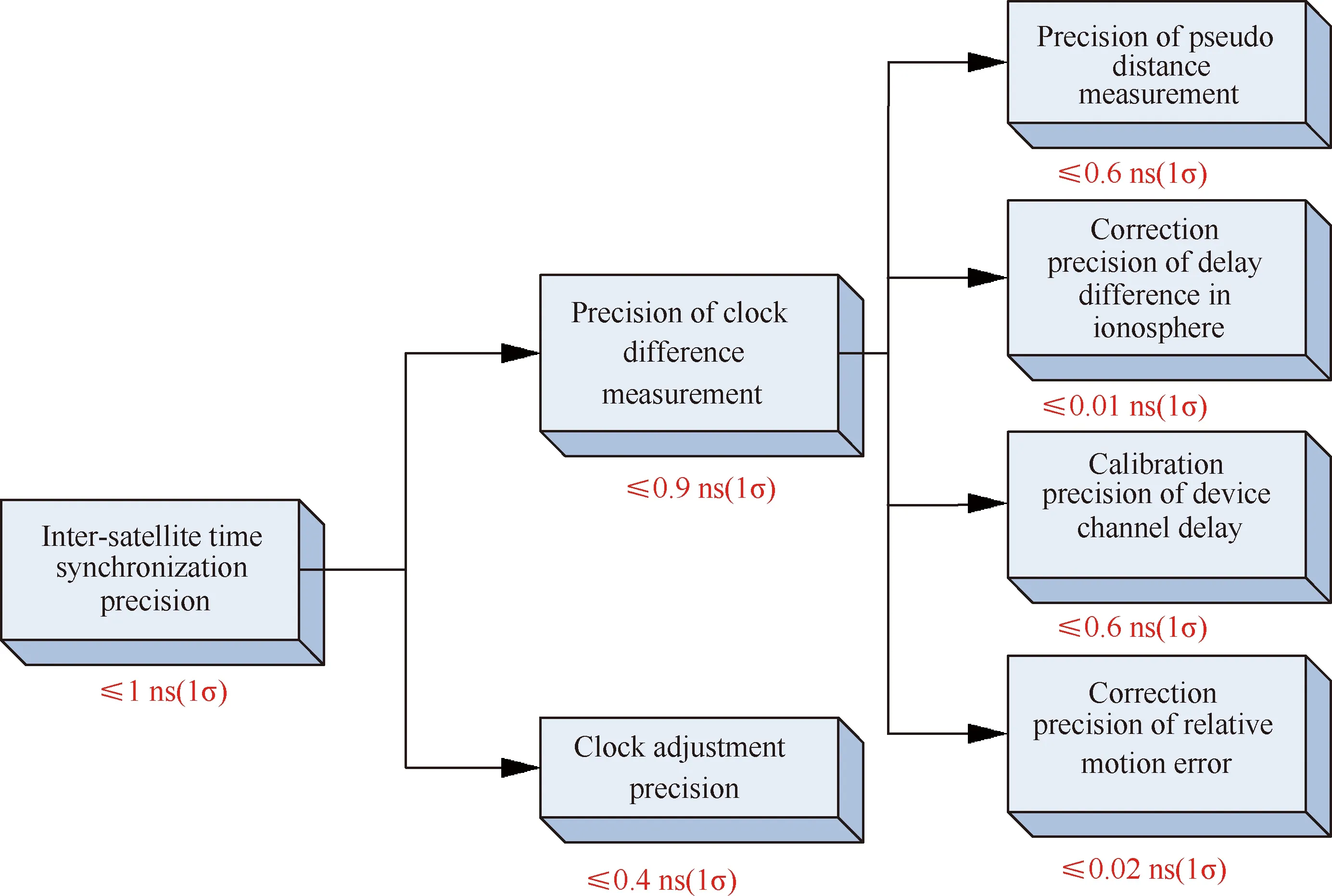
图3 指标分解Fig.3 Index decomposition
具体末端指标精度的分配原因和可行性分析见3.1~3.5节。
3.1 伪距测量精度
1) 热噪声颤动
采用延迟锁相环路(Delay Lock Loop, DLL)实现伪码跟踪,由热噪声引起的码跟踪抖动标准差为
(16)
式中:Bn=2 Hz为码环的噪声带宽;G(f)为信号的功率谱密度,归一化到无穷带宽上的单位面积内;Bf=30 MHz为双边前端带宽;Tc=1/10.23 MHz为码片周期(s);Δ=0.1 chips为早迟相关器间隔;Tp=1 ms为预检测积分时间;C/N0=42 dBHz为载噪比。
则热噪声引起的1σ伪码相位测量误差为0.008 2 chips,折合0.801 6 ns。
2) 动态应力误差
当采用非经载波环辅助的3阶码环时,其动态应力误差为

(17)
式中:d3R/dt3=6.6 mm/s3为最大视线方向加加速度动态;Bn=2 Hz为码环噪声带宽。
则1σ伪码相位测量动态应力误差为0.398 3 mm,折合1.3 ps。
3) 总的相位测量误差
由以上分析估算得到:当采用3阶伪码跟踪环时,总的伪码相位测量误差为
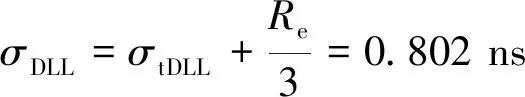
(18)
采用载波相位平滑伪距技术,其1σ误差约为

(19)
式中:测距码的速率为10.23 Mcps,对应码片长度为29.3 m;载波的频率分为主从两星,主星频点为3 201.99 MHz,对应载波波长为0.094 m;从星频点为3 375.9 MHz,对应载波波长0.089 m;Tsmooth为平滑时间窗口宽度;Bn=2 Hz为码环滤波器带宽;σDLL=0.802 ns为码环跟踪误差。类似地,求得载波锁相环跟踪误差σPLL=4.88 ps。如表1所示,当平滑时间窗口宽度大于2 s时,可获得优于0.3 ns的伪距测量精度。因此本文伪距测量精度分解指标为0.6 ns是合理可行的。
针对动态场景下可能引起的失锁失周问题,本文选用双星编队轨道,具体卫星动态参数可参见5.1节,根据参数可见星间距离变化范围较小,不会引起功率突变问题,星间相对动态也较小,因此不会频繁引起失锁失周的现象;此外,若发生接收机失锁失周等问题时,可通过目前较为常用的双频伪码/载波相位组合方法重新求得宽巷与窄巷相位观测值的整周模糊度,或对接收机进行复位操作,在30 s内即可完成信号的捕获和环路锁定跟踪。
时钟调整部分由于设置了野值突跳检测功能,将会根据环路失锁前的状态进入保持状态,等待环路重新稳定后再次进入跟踪调整状态,保证系统不受环路失锁失周的影响。
表1 平滑窗宽度与测距精度
Table 1 Width of smooth window and precision of distance measurement

Smooth time/sPrecision of pseudo distance measurement after smoothing/ns10.420920.2755100.1168200.0822300.0670
3.2 电离层时延误差修正精度
由于电离层传播延时具有频率选择性,即不同的频点对应于不同的路径传播延时,因此会引起非零的双向路径传播延时差。本文采用双频电离层校正技术消除电离层影响。
R1、R2、θ1和θ2分别为f1、f2载波频点上伪码测距值和载波相位测量相位;ρ为星间距离。则忽略其他误差项后有
(20)
(21)
联立式(20)和式(21),可解得无电离层误差的伪码伪距和载波伪距测量量为
(22)
ρ无电离层,载波伪距=
(23)
事实上,双频电离层校正技术仅能消除电离层传播延时误差的一阶小量。有研究表明[26],电离层传播延时误差的一阶小量比较大,约为百ps量级;而二阶小量非常小,优于0.1 ps。因此双频电离层校正技术能够有效消除电离层传播延时误差的一阶小量,因此可获得优于0.01 ns的电离层时延误差修正精度。
根据式(22),设主从卫星伪距观测量的1σ标准差都为σ(二者近似相等)且设所有误差源互相独立,则可得电离层修正后伪距误差的1σ标准差为
σ无电离层,伪距=

(24)
结合本文实际频点进行计算,主星电离层修正后伪距误差为修正前的1.94倍;从星电离层修正后伪距误差为修正前的1.84倍。
根据本文3.1节的讨论,通过一定时间的平滑,载波相位平滑伪距精度比伪码直接测距精度可以提高一个量级,达到0.1 ns量级,并且随着历元数的增加,平滑效果更加明显。由此可见,通过双频修正后,虽然噪声放大为原值的2倍左右,但依然可以满足距离测量精度优于0.6 ns的指标要求。
3.3 收发信机通道时延校准精度
设备时延校准技术的难点在于收发通道时延的分离标定。利用包络检波方法,结合伪码相关测距的原理提供高精度的扩频收发信机的收发通道时延测量结果。作者在研制某型号项目过程中,发明了一种收发通道时延自校准方法,可取得优于0.6 ns量级的时延标定精度,该发明已申请国防发明专利[27]。由于篇幅所限,该部分内容不再赘述。
3.4 相对运动误差修正精度
由于主星和从星相对运动,因此路径传播延时是个随时间改变的函数,从而导致双向路径传播延时不再完全相等,从而造成非零的双向路径传播延时差。本文采用基于多普勒频移的运动补偿技术消除该误差。
图4为相对运动对双向距离测量的影响示意图。设主星M发出测距信标时,主星M和从星S之间的距离为R2;从星S发出测距信标时,主星M和从星S之间的距离为R1,且两者的时间同步误差为Δt,主星M和从星S在其连线上的径向速度分别为rvM、rvS,则根据刚体运动学理论,可以得到方程组:
(25)
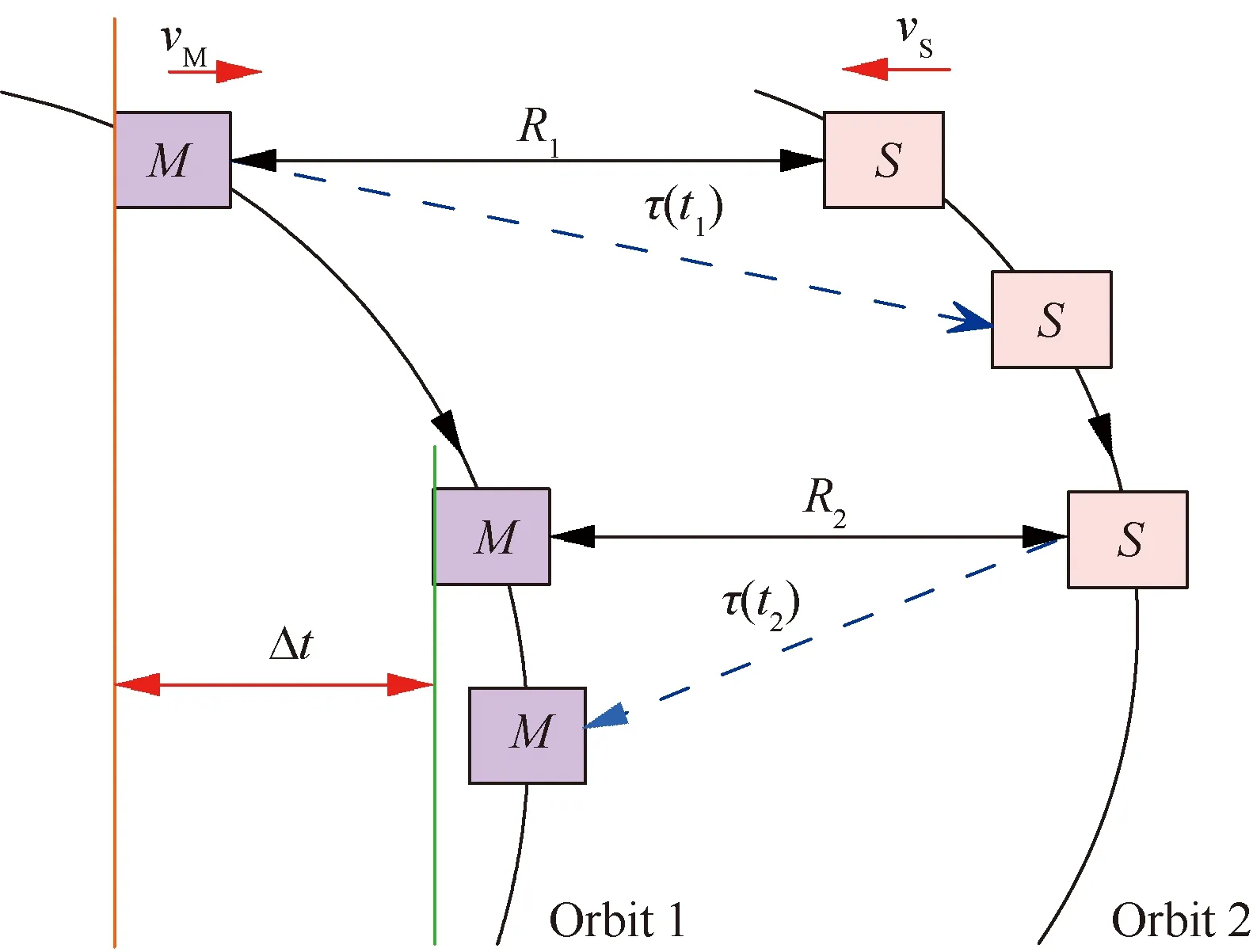
图4 星间相对运动对距离测量的影响示意图Fig.4 Influence of relative motion between satellites on distance measurement
式中:c为光速
不妨设主星M和从星S的径向速度变化相对缓慢,在测量时间内可假定其为匀速运动,由式(25)可得由相对运动造成的双向路径延时差为
Δτ=0.5[τ(t2)-τ(t1)]=
(26)
不妨考虑编队飞行场景,设主星M和从星S的最大距离为300 km,最大相对运动速度分别为rvM=-rvS=3 750 m/s。代入式(26)可知,由同步时间间隔引起的测量误差项优于1.25 ps,不用修正;而由多普勒引起的测量误差项约为11.67 ns,必须进行修正。
校正方法是估计径向速度rvM和rvS,并据此修正由多普勒引起的测量误差项。不妨设实时测速精度达到5 cm/s,则校正后的由多普勒引起的测量误差项优于0.2 ps,证明分解的相对运动误差修正精度要求合理。
3.5 时钟同步控制精度
针对时钟相位调整精度0.4 ns的技术指标,采用数字延迟线实现,用来调节1PPS与10 MHz之间的相位差。本文采用数据延迟线技术(Data Delay Devices, DDD)的可编程延迟线3D3428-0.25。其相位调节范围为63.75 ns,调节精度为0.25 ns,满足本文所分解的技术指标。
4 时间调整环路关键参数选择
利用双向测距技术,通过载波相位平滑、相对运动补偿、设备时延在轨校准、双频电离层修正等技术消除测距、延时等因素引起的误差,使从星可以收到长期平均准确度和稳定度较高的星间钟差值。利用频率驾驭算法计算出晶振压控端的电压数字量,进而通过高分辨率的D/A转换器输出该控制电压,达到校正晶体振荡器输出频率的目的,使晶振的振荡频率锁定在主星时钟上。
根据以上时间调整环路工作过程,剥离时钟同步环路两个重要参数:频率调节量及时钟调整周期。
1) 频率调节量:在时钟闭环调整的过程中,频率调节量过大会对晶振的频率稳定度产生破坏性影响,导致时钟不可用;调节量过小则无法补偿两钟之间的钟漂,导致无法收敛。
2) 时钟调整周期:需满足时钟相位和频率的同步收敛,同时保证快速闭环收敛。
本文所用晶振为筛选过的203所ZF549型号晶振,主要仪器设备见表2。后续分析论证均依据所选用晶振指标开展。

表2 主要仪器设备Table 2 Main instruments
4.1 频率调节量
考虑试验所用晶振的秒稳约为σosc=1×10-12,工程应用上为了避免破坏晶振自身稳定度,设定调整后时钟频率稳定度σ应控制在原稳定度的1.05倍以内,即1.05×10-12。这样的设定下,频率调节后的秒稳为
(27)
可得,当频率调节量σadjust小于3.2×10-13时,调节对晶振秒稳的影响可以忽略不计。
4.2 时钟调整周期
首先从相位角度,考虑时钟调整周期对相位差变化的影响。假设一个调节周期开始时的相位差为700 ps,调整周期为τ。那么根据指标要求,经过一个调整周期后,系统的相位差应当小于1 ns:
0.7+A1τ+1/2(A2τ2)≤1
(28)
式中:A1为预计经过频率驾驭后的晶振输出频率准确度;A2为拟采用的晶振老化率。取A1=2×10-13,A2=2×10-10/天=2.3×10-15/s。由式(28)得到时钟调整周期τ≤385 s。
其次从频差角度考虑。假设当前一个调节周期开始时的频差为2×10-13。那么经过一个调整周期后的频差应当小于频率调节的最大值3×10-13。因此有以下关系:
2×10-13+A2τ≤3×10-13
(29)
τ≤43 s
(30)
一般来说频率调节时间间隔越短,系统控制带宽越宽,响应越快。但双向时间比对数据传输及数据处理会引入一定的时延,过高的控制频率对改善系统响应没有效果。再者高质量的晶振自身的短期稳定度较好,过高的控制频率会对其短稳造成影响。
另一方面,如图5所示,依据双向测距和时间传递技术的原理可知,假设主从星钟差为Δt,从星在tn+Δt+1时刻收到主星tn时刻的信号,得到tn时刻的从星伪距测量值;同时主星在tn+1时刻收到从星tn时刻的信号,得到tn时刻的主星伪距测量值;随后主星在tn+2时刻通过电文向从星发送其tn时刻的主星伪距测量值;从星在tn+Δt+3时刻收到该电文,经过与之前保存的从星伪距测量值比对,得到tn时刻的两星间钟差,并在本秒内进行时钟调整。由此可知,每次时钟调整需经过3 s才能反映到钟差测量结果上,因此,结合上述最大时钟调整周期,本文确定了时钟调整周期为3~43 s。为保证同步环路收敛速度,工程上选取3 s为时钟调整周期。

图5 钟差传递过程Fig.5 Process of clock bias transfer
5 高精度时间同步测试验证
5.1 实验环境构建及测试设备组成
实际测试系统组成如图6所示包括:主从卫星收发信机、信道模拟设备、铷钟、时间间隔计数器、直流稳压电源、示波器、相噪仪等。
其中主从卫星收发信机采用全双工双频BPSK的通信体制进行双向通信测距、得到钟差后从星进行时钟调整,伪码速率为10.23 MHz,伪码周期为1 ms,载噪比固定为42 dBHz,数据速率为1 Kbps,主星射频频点f1=2 056.23 MHz,f2=3 201.99 MHz;从星射频频点f3=2 230.14 MHz,f4=3 375.9 MHz。
信道模拟设备选用dBm公司的SLE900,用于模拟双星编队飞行运动场景,星间距离变化如图7所示,为130~520 km,卫星动态特性如表3所示。通过数学仿真建立大气层、电离层等空间模型,利用数值内插法,将各项引起的误差参考量插入信道,同时完成功率控制功能。
测试系统主要仪器设备性能指标如表2所示。

图6 测试系统组成Fig.6 Composition of experimental system
5.2 开环非调钟状态下钟差测量试验结果
在测量跟踪环路稳定后,可以稳定输出双向测距钟差,在利用该钟差进行时钟调整前,应对钟差测量的准确度与精度进行测试。在晶振自由运行模式下进行测试,图8(a)为通过双向测距后从星解算得到的钟差,图8(b)为时间间隔计数器输出的两收发信机间的钟差,二者在同一次试验中测得且为同时间段内的测量数据。经统计,铷钟与压控晶振相对时钟钟速约为0.9 μs/s,钟漂可以忽略不计。图8(c)为利用双向测距解算的钟差与时间间隔计数器输出钟差对应时刻的差值,忽略时间间隔计数器25 ps的精度误差,可以认为时间间隔计数器输出钟差为准确参考值,经计算,双向测距得到的钟差精度(1σ)为315 ps左右。验证了双向测距解算钟差的准确度与精度符合前文指标分解,可以为后续闭环调钟提供依据。
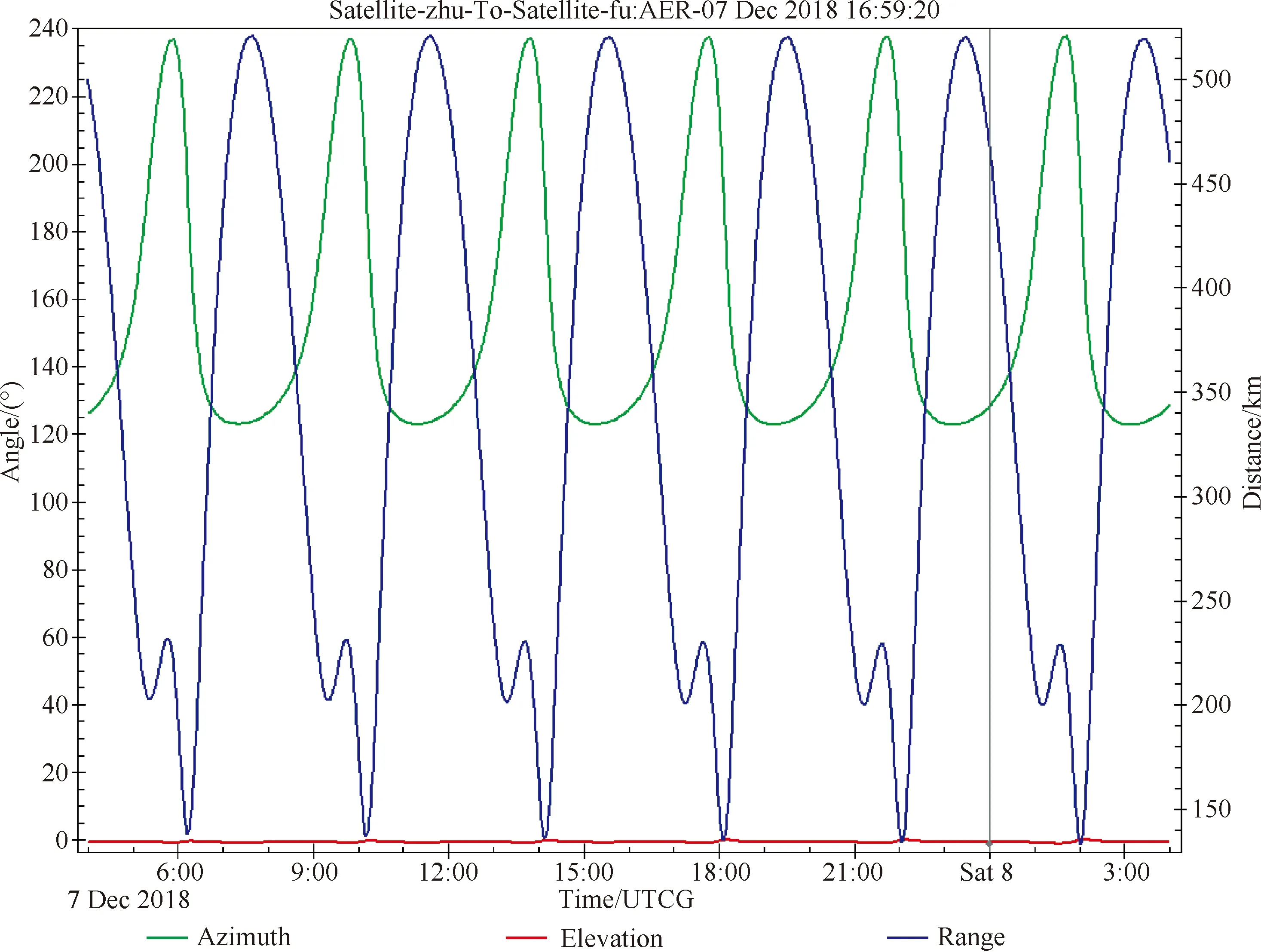
图7 星间距离变化Fig.7 Inter satellite range variation
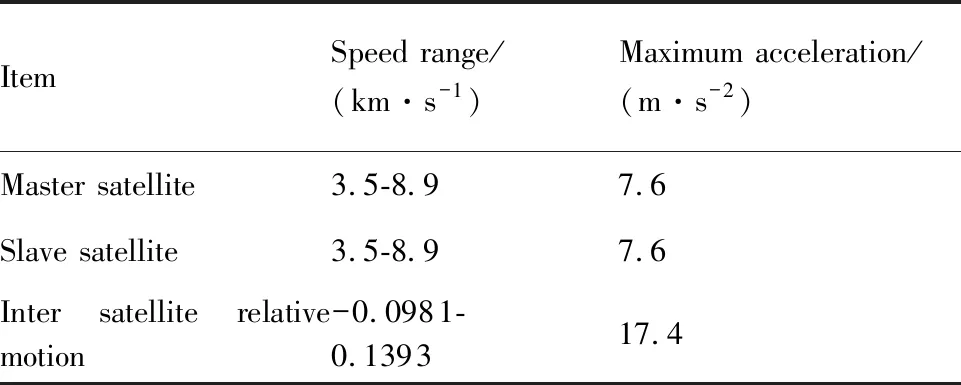
表3 卫星动态特性Table 3 Satellite dynamic characteristics


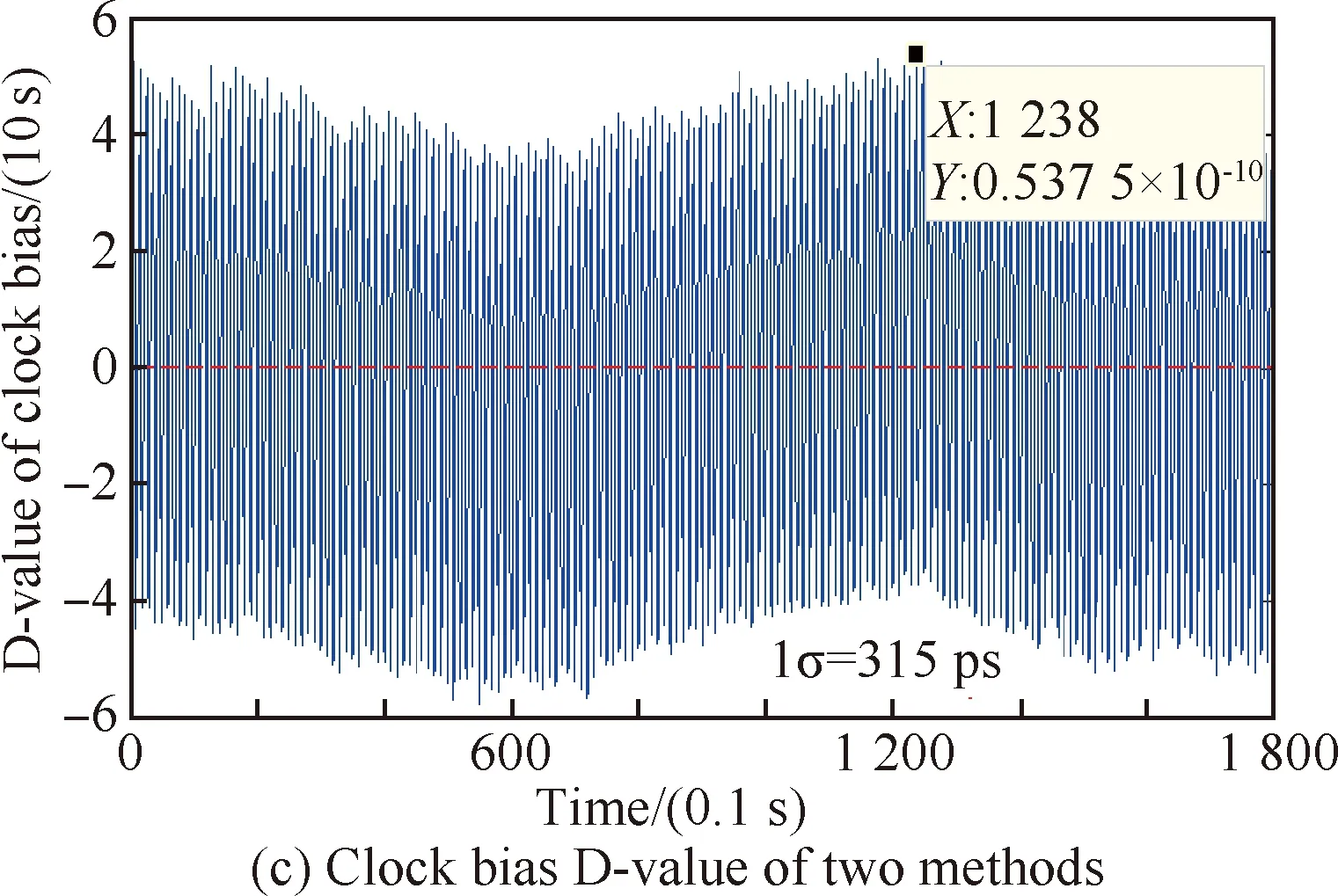
图8 开环非调钟状态下钟差测量结果Fig.8 Results under open loop non-adjustment state
5.3 闭环调钟试验结果
5.3.1 单次闭环调钟试验
基于晶振自由状态下的测试结果,对时钟调整结果进行闭环测试,同样采用双向测距结果与时间间隔计数器输出两种统计结果进行比对。图9 为时钟闭环调整稳定后,时间间隔计数器与双向测距输出钟差。
图10为日本2009年RESSOX系统公布的通过地面原子钟调控星载高稳石英钟以实现星地时间同步的结果[2],其时间同步精度最小为2 ns。与RESSOX系统相比,本文时间同步误差结果为768 ps,具有更高的时间同步精度。

图9 时钟闭环调整稳定后时间间隔计数器与双向测距输出钟差准确度对比Fig.9 Comparison of clock bias accuracy of sr620 and two-way ranging under stable state

图10 RESSOX系统闭环调整稳定后时间同步精度Fig.10 Time synchronization accuracy of RESSOX system under stable state
5.3.2 多次闭环调钟统计试验
如图11所示,本文采用不同标定过的测试线缆进行30次测量,经统计,得到其时间同步误差(调钟稳定后均值)为793 ps。
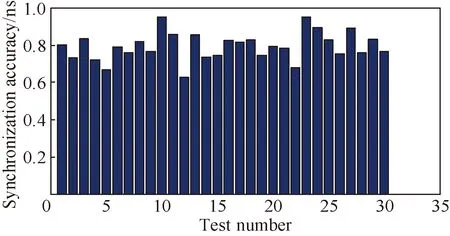
图11 时间同步准确度统计Fig.11 Statistics of time synchronization accuracy
5.3.3 闭环调钟长时间稳定性试验
图12为系统长时间运行的同步误差统计,从时间同步误差进入5×10-9后的1 h开始进行统计,可得时间同步系统进行稳定状态后10 h内其时间同步1σ为417 ps,达到了1 ns的预期指标,且系统连续工作稳定可靠。
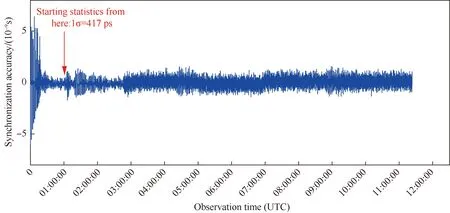
图12 时间同步系统长时间运行精度Fig.12 Time synchronization accuracy in long term statistics
6 结 论
本文提出一种适用于未来在轨卫星系统的高精度时间同步方法,建立了地面试验系统并完成了测试验证,得到以下结论:
1) 建立了基于钟差测量环路与时钟同步环路的时间同步系统模型,给出了高精度时间同步方案及分解指标。
2) 该方法独立于导航或地面授时手段,具备自主性和连续性。
3) 该方法可以有效提高卫星系统时间同步精度至1 ns以内,同时具备较强的空间应用价值和工程转化能力。
本文的地面试验系统搭建过程中,已考虑了伪距测量时延误差、相对运动引起的时延误差、设备零值时延误差、电离层时延误差等主要误差信息。面向未来空间应用,仍可能存在以下特殊情况,需要结合实际工况进一步讨论:
1) 微重力环境下,卫星暴露在太阳辐射下会受到一定的光压,光压强度取决于卫星质量和辐照面积。长期在轨的卫星受到太阳光压作用,会引起米级甚至是几十米的位置偏差,是未来在轨实际应用时必须考虑的情况。
2) 根据相对论理论,若以静止时钟为参考时钟,那么高速移动的时钟计时会变慢,这种影响较多体现为二阶多普勒变化。后续面向应用,需结合实际卫星轨道参数、Sagnac效应、相对运动速率等情况进行补偿修正。
