采用改进的CE/SE方法模拟方管中氢氧爆轰波的稳定传播结构

2019-05-24沈洋刘凯欣陈璞张德良

航空学报 2019年5期

沈洋，刘凯欣，陈璞，张德良

1.北京大学工学院，北京 100871 2. 中国科学院力学研究所高温气体动力学国家重点实验室，北京 100190

爆轰是一个包含了复杂化学反应的流体动力学过程，由于在建筑工程、能源生产、国防建设等领域的重要应用，爆轰波的起爆和传播机制，特别是胞格结构形成机理，仍然是当下热门的研究方向。目前关于一维爆轰波的理论模型已构建完善，对于平面气相爆轰波传播的研究也已经相当成熟，学者们把目光越来越多地聚焦到爆轰波三维结构的研究上面。Hanana等[1]在考察方管中爆轰波传播压力结构时，使用烟熏法得到了管壁上胞格结构的清晰图样。经过细致的分析，他们认为方管中爆轰波传播具有两种稳定的结构：对角模式和直角模式。除此之外，周凯等[2]利用爆轰驱动技术与膨胀管的结合，设计并初步研究了高速气流爆轰驱动膨胀管。Zheng和Wang[3]通过实验考察了低温等离子体对爆燃转爆轰过程的加速作用。这些都是实验研究三维爆轰波形成与传播的重要尝试。

由于实验技术的限制，想要捕捉三维管道内部爆轰波复杂结构的细节信息目前来讲仍有些困难。相比实验手段，数值方法的最大优势是可以获得任意物理量在任意时刻的全局分布，但由于三维模拟需要的网格数以千万计，计算量也是一个不容忽视的问题。在模拟爆轰波传播过程中的一个关键问题是选择合理的化学反应模型。Oran 等[4]提出了基元反应模型并用来考察平面氢氧爆轰的胞格结构。Sichel等[5]在Taki和Fujiwara[6]的二步模型基础上引入了考虑气体组分变化的参数，并在氢氧爆轰系统的算例中给出了具体的公式，提高了二步模型的计算精度。

Tsuboi等[7-8]采用基元反应和non-MUSCL(non-Monotonic Upwind Scheme for Conservation Laws)格式对Hanana的方管实验进行了数值模拟，发现能够得到有效数值结果的管道尺寸比爆轰实际的胞格尺寸要小，另外他们还对在圆管中的旋转爆轰进行了数值模拟[9-10]。窦华书[11-12]和王成[13-14]等用一步模型和五阶WENO(Weighted Essentially Non-Oscillatory)格式对三维爆轰波在方管中的传播进行了进一步的数值分析，发现爆轰波在较小尺寸的方管中也存在类似于圆管中的旋转传播模式。另外，翁春生和Gore[15]、申华[16]、Ivanov[17]、蔡晓东[18]以及黄玥[19-20]等同样对方管中爆轰波的传播做了详尽的数值分析并且得到了类似的结论。然而，绝大部分的数值模拟工作需要高阶精度的数值格式和细致的化学反应模型来获得较好的胞格图案，否则得到的结果将不够清晰，而本文采用的时空守恒元/解元(CE/SE)算法是兼顾计算效率与质量的一种高精度数值格式。

时空守恒元/解元算法是近年来兴起的一种全新的求解双曲守恒型方程的计算方法，将时间和空间统一起来同等对待，巧妙地定义时空间的守恒元和解元使得局部和全局都严格保证守恒率。NASA Lewis研究中心的Chang[21]首先提出这种差分格式，并将其推广到二维情况[22]。Wang[23]针对含有激波的气动声学问题，对CE/SE算法的计算精度进行了分析。Zhang等[24]基于四边形网格划分方案改进了守恒元和解元的结构，并由此顺利推广到了三维情况。

本文针对三维氢氧爆轰问题，使用基于四边形网格划分方案的改进时空守恒元/解元格式和Sichel新型二步化学反应模型，以较小的计算代价得到了方管中3种稳定传播模式的爆轰波结构，并着重于讨论截面尺寸在两种传播模式下对管道中爆轰波结构稳定性的影响。

1 基本方程组和化学反应模型

爆轰波传播是爆轰间断以超声速在流体中传播的过程，在数值模拟时，一般情况下可以不考虑热传递和黏性效应，因此流体力学基本方程组实际上就是欧拉方程和描述化学反应的方程组成的方程组。

在三维笛卡儿坐标系中流体力学基本方程组和二步反应模型可以表示为

(1)

式中：流矢量U=[ρρuρvρweραρβ]T，ρ为密度，u、v、w分别为速度矢量在笛卡儿坐标系中沿x、y、z3个方向的分量，α和β分别为诱导和放热反应的进行度(初始为0，反应完全为1)，e为单位体积的总能；E=[ρuρu2+pρuvρuw(e+p)uραuρβu]T，p为压强；F=[ρvρuvρv2+pρvw(e+p)vραvρβv]T；G=[ρwρuwρvwρw2+p(e+p)wραwρβw]T；刚性源项S=[0 0 0 0 0ωαωβ]T，ωα和ωβ分别为诱导和放热反应的速率。流矢量E、F、G均为U的函数，e的表达式为

(2)

式中：Q为单位质量的氢氧燃烧热；γ为氢气的比热容比。

Sichel等在氢氧混合系统下构建的改进二步模型[5]分为两个步骤。第1步描述了一个以自由基形成为特征，无显著能量释放的诱导期，经过详细比较，在诸多现有的模型中选择了Burks和Oran提出的反应模型，得到了拟合式(3)。第2步描述了产生燃烧产物与释放大量热量的放热反应期，在这里，通用Arrhenius公式式(4)被认为是对氢氧混合气体放热反应的最准确描述。通过再现基元反应模型所描述的化学动力学模型的性质，可拟合得到Arrhenius公式具体的输入参数。

(3)

(4)

2 数值方法和差分格式

爆轰波是含有化学反应的强间断流动，对于数值模拟的精度，特别是强间断面附近的模拟精度要求很高。CE/SE方法用于三维爆轰波的数值模拟有着得天独厚的优势：首先，相比传统差分方法，它从控制方程的时空积分形式出发，在时间和空间上都能够很好地保证物理量的守恒性；其次，通过巧妙的守恒元解元的设置以及权函数的引入，其在捕捉爆轰波的强间断方面具有良好的效果；最后，通过改进的守恒元解元划分，格式很容易推广到三维情况。总的来说，CE/SE格式是一种保持高精度和低计算量的具有极高性价比的数值格式。下面在三维一阶Taylor展开CE/SE格式[16]的基础上推导二阶Taylor展开下三维CE/SE递推格式。

由于二步模型的化学反应弛豫时间比CFL(Courant, Friedrichs and Lewy)时间步长小1 ～ 2个数量级，因此采用化学反应与爆轰推进解耦的方法，在推导格式时，不必考虑源项的作用。根据散度定理,守恒方程可以写成积分形式：

(5)

式中：张量H={U,E,F,G}为时空间上流矢量的组合；S(V)为任意封闭的时空体域V的边界；ds=dσ·n，其中dσ和n分别为边界S(V)的面积和外法向。利用解元[16]在网格基点的二阶Taylor展开，并让展开式在守恒元[16]上进行积分，代入式(5)，最终可以得到U的半步递推格式：

(6)

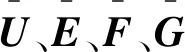
式中：算符±a、 ±b、 ±c是相互独立取正负的；而算符±a和∓a意味着其中一个取正号时，另一个则取负号；对a、b、c的求和表示对算符±a、 ±b、 ±c穷举所有正负；符号“∧”代表一个重定义的函数。流矢量N重定义函数的第m项分量在点A的展开为

(7)

(8)

如此，就能利用递推格式得到下半步空间流矢量U的数值解。进一步利用解元物理量在交界点处的连续性，可得到下半步U的x、y、z方向导数的迎风和逆风表达，再利用权函数得到方向导数的一个加权结果，就能将此递推格式循环下去。

3 数值模拟通用条件

实验表明爆轰波具有非常复杂的三维结构，主要包括前导激波、马赫杆(MS)、横波(TW)等，它们相互作用形成了爆轰波阵面。爆轰波阵面具有不稳定性同时又具有时空周期性，爆轰波阵面的周期性变化形成了所谓的胞格结构，体现了爆轰的很多特征参数，但是其机理仍未完全探明，因此爆轰波传播形成的胞格结构是爆轰波研究的一个热点。

本文针对方管中爆轰波传播的物理问题进行数值模拟。影响方管内爆轰波稳定传播结构的因素有很多，本文重点研究截面尺寸在两种传播模式下对爆轰波稳定传播以及形成的胞格结构的影响，对于其余控制变量采用统一的设置。以下是本文程序所使用的通用模拟条件。

1) 初始条件：在管道左侧5%的区域设置p=50p0,ρ=ρ0的高压区，其余空间则充满了p0、T0、ρ0的氢氧混合气。其中p0=105Pa,T0=298 K,ρ0=p0/(RT0)，在本文中氢气与氧气以2:1的摩尔比相混合，因此混合气体常数R=689 J/(kg·K)。整个空间处于静止的状态，在计算开始时隔板消失。

2) 边界条件：与管道方向平行的4个壁面以及左边界都使用反射边界条件，右边界使用自由边界条件。实际上右边界条件的设置对计算结果没有任何影响。

3) 网格设置：为了找到合适的计算网格，首先对网格尺寸d=1/10,1/25,1/50 mm 3种网格密度的方管算例进行了试算，然后对数值结果进行了比较。不同网格密度下侧壁胞格结构如图1所示，所谓的胞格结构在数值上即为压力历史极值在壁面上的分布。结果显示，当截面尺寸(D)在2 mm及以上时，d=1/25 mm的网格密度已经足够满足计算需求；但当截面尺寸为1 mm时，d=1/25 mm得到的胞格结构相比d=1/50 mm 的结果稍显模糊，因此将网格密度加倍。

图1 不同截面和网格尺寸下历史压力极值在方管上表面的分布(对角模式)Fig.1 Distribution of maximum pressure histories on upper surface of square duct with different cross-sectional sizes and grid sizes (diagonal mode)

4) 方管长度设置：当截面尺寸较小时(≤2 mm)，爆轰波形成稳定传播模式可能会出现较长的过渡区，此时方管长度用160 mm为宜，一般情况下80 mm即能出现稳定的爆轰波结构。

5) 初始扰动设置：为了形成横波，在初始30个时间步的化学反应区内(0<β<0.99)对内能e给予小幅度的正弦扰动。扰动分为沿着边界的直角模式和沿着对角线的对角模式，其无量纲化的扰动幅度e′/e在方管yz截面的分布函数如图2所示(δ为扰动幅度极值)。

图2 方管中两种扰动模式在yz截面上的振幅分布Fig.2 Amplitude distribution of two kinds of perturbation modes on yz section of square duct

图3 不同扰动幅度下历史压力极值在xy侧壁的分布(对角扰动，D=2 mm，d=1/25 mm)Fig.3 Distribution of maximum pressure histories on xy sides with different amplitudes of perturbation (diagonal mode, D=2 mm, d=1/25 mm)

为了确定适合本文数值模拟的扰动振幅δ，对图1(a)中的算例(网格尺寸为1/25 mm)分别给予不同的扰动幅度(δ=0.01, 0.05, 0.50)进行试算，结果如图3所示。可以看到当扰动幅度δ= 0.50时，爆轰波已经失稳，模拟产生了非物理的结果；而当扰动幅度δ= 0.01时，形成的爆轰胞格图案相对比较模糊。最终选择δ= 0.05作为本文方管爆轰数值模拟的振幅。

6) 并行设置：对方管轴向进行分割，相邻的计算块保留界面附近的两层数据以作通讯，利用MPICH2接口的通讯函数形成多线程并行计算。

4 数值结果分析

4.1 不同截面尺寸的算例比较

不同的传播模式下，截面大小对胞格结构尺寸的影响不尽相同。利用如图2所示的初始扰动形成直角和对角传播模式。在控制其他变量不变的情况下方管的截面尺寸在1～8 mm范围内改变。截面尺寸为2～8 mm时，网格尺寸均为1/25 mm；截面尺寸为1 mm时，为了保持最终结果的精度，网格尺寸加密为1/50 mm，所有算例的计算参数如表1所示。将表1中所有算例的xy侧壁截面胞格结构绘制在一起，如图4所示。

观察图4(a)中对角模式算例1-1～算例1-6的模拟结果可以发现，当截面尺寸在3～8 mm浮动时，稳定的爆轰波结构在壁面均投影出一个胞格宽度，胞格数目没有改变，胞格尺寸与截面尺寸相对应。当横截面尺寸减小为1 mm 时，爆轰波结构将会从对角模式逐渐转变为螺旋模式。

表1 不同算例的模拟参数Table 1 Simulation parameters in different cases

如果给予初始直角扰动，通过截面尺寸的变化得到算例2-1～算例2-5，其模拟结果和对角模式结果有一些差别。当横截面尺寸增加至8 mm时，较大的截面尺寸拉伸爆轰波传播结构，使得横波分裂并逐渐累积相位差，最终胞格结构分裂成为两个较小的胞元。另外，当横截面尺寸减小为2 mm乃至1 mm时，爆轰波结构将会从直角模式转变为螺旋模式。

以上数值结果指出，方管尺寸变化虽然可以使胞格尺寸随之产生适应性的变化，但存在一定的极限。通常来讲，胞格尺寸越小，横向胞格个数越少，胞格结构越稳定。但保持小胞格尺寸和维持横向胞格数是矛盾的，若横向胞格数目增加一倍，则胞格尺寸必然减小一半，而随着截面尺寸的变化，这两个因素的主导地位也会随之产生变化。

当方管截面尺寸只增加一点时，维持横向胞格数目成为维持胞格结构稳定性的主导因素，所以胞格尺寸会相应的增大以保证横向胞格数目不发生变化。

图4 不同截面尺寸算例典型区域的xy截面胞格结构Fig.4 Cellular patterns in typical areas on xy sides with different cross-sectional sizes

当方管截面尺寸增加过大，保持小的胞格尺寸则成为了维持胞格结构稳定性的主导因素，此时胞格图样分裂成更多的横向胞格以保证每个胞元的小尺寸。

另外，几何性质决定胞格结构总是在壁面边界拥有整数或者半整数个胞格，也即鱼鳞状或者半鱼鳞状的图案；而直角模式中，由于横波平行于壁面进行扫掠，因而永远不会出现半整数的胞格结构。

最后，当截面尺寸足够小时(1 mm)，则不管初始扰动条件如何，稳定的爆轰波传播结构都会转变为螺旋模式，旋转方向是顺时针还是逆时针取决于初始扰动形式。临界情况下(2 mm)，对角模式会在计算区域后半段衰减为半胞结构，而直角模式则会在区域中部形成四头螺旋的中间传播态，并最终转化为螺旋模式。关于螺旋模式旋转方向以及临界尺寸下爆轰波结构变化将在下文进行详细的讨论。

在考察截面尺寸对方管氢氧爆轰波传播结构的影响时，扰动形式是一个不可忽略的因素。乍一看这似乎只是一个数学游戏，没有过多的物理意义，然而数值模拟结果表明，无论初始给予什么扰动，随机扰动，非对称扰动，正弦扰动还是矩形扰动，最终的传播模式总是有规律可循，或者是对角模式，或者是直角模式，或者是螺旋模式。究其原因，可能是初始扰动横波在数学上可以表达为不同频率和振幅的傅里叶级数，但是在扰动传播过程中，与方管尺寸不相容的频率项都受到强阻尼而衰减了，最终留下特定频率的扰动与爆轰波相互正作用形成主要项，这类扰动项最终形成了所观察到的爆轰波传播结构。

表2给出了不同截面尺寸在两种传播模式下对爆轰波胞格结构的综合性影响。

表2 截面尺寸在两种传播模式下对爆轰波胞格结构的影响

Table 2 Effect of cross-sectional size with two kinds of propagation modes on cellular patterns of detonation wave

D/mm胞格结构对角模式直角模式1(很小)顺时针螺旋逆时针螺旋2(临界情况)对角→半胞结构直角→四头螺旋→单头螺旋>2(适中)对角直角

4.2 方管中的3种稳定结构

为了验证CE/SE算法搭配Sichel改进二步模型的可靠性，从表1的所有算例中选取了4个典型算例(算例1-1，算例1-4，算例2-1，算例2-4)，用来考察方管中的3种稳定传播模式：对角模式，直角模式和螺旋模式，并用本文的模拟结果与前人的结果进行比较。图5给出了方管中3种稳定传播模式在一个周期内的压力等值面演化过程。

在图5(a)和图5 (b)中，计算区域为80 mm×4 mm×4 mm，初始分别给予对角扰动和直角扰动。从等值面演化过程中可以看出，爆轰波在传播过程中，前导激波与横波(TW)交汇形成一些三波线(TL)，其轨迹在壁面形成鱼鳞状的图案，即胞格结构；前导激波波阵面的各区域被三波线交替分割为凸离爆轰方向的马赫杆(MS)和相对凹陷的入射波(IS)。相邻三波线对撞、分离使得新的马赫杆不断产生，旧的马赫杆衰减为入射波。在对角模式图5(a)中，两组共8条三波线形成两个封闭的长方形，彼此相互垂直且与通道壁面呈45°。类似的，在直角模式图5(b)中同样存在两组共4条三波线，两组平行线彼此相互垂直，且各自平行于壁面。在每个胞格周期内，当一组三波线扫掠至平行的壁面附近时，会在另一组三波线形成的壁面胞格结构中显示出横向的亮线，称为拍波(Slapping wave)，以此作为直角模式和对角模式胞格图案最为显著的不同之处。在图5(c)和图5(d)中，分别给予和图5(a)、图5(b)相同的初始扰动，但是把截面尺寸减少至1 mm。计算结果显示存在两种类似的螺旋结构，一种沿顺时针螺旋，另一种沿逆时针螺旋。此时只有一对相互垂直且正交于壁面的三波线存在。和图5(b)的直角模式不同之处在于这一对三波线存在大约π/4的相差，失去了轴对称性质，如图6所示。如果观察此时的三维爆轰波结构，会看到一条明亮的压力极值带沿着管壁进行螺旋运动，在管道内部则没有明显的压力集中区域，如图7所示(图中pmax为历史压力极值)。

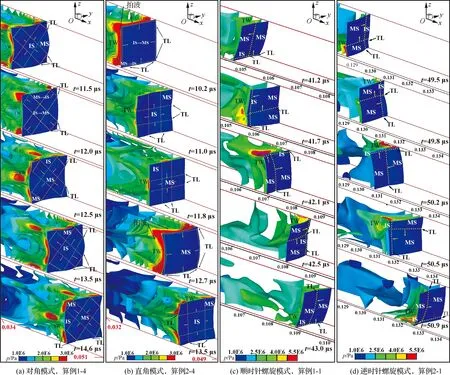
图5 约一个周期内的压力等值面演化过程Fig.5 Evolutionary process of pressure iso-surfaces during about one period

对于螺旋模式的旋转方向，有顺时针的模拟结果，也有逆时针的结果。窦华书等[11]使用随机扰动和一步反应模型，得到的模拟结果是顺时针螺旋；王成等[13]使用沿着对角线的正弦扰动和一步反应模型，得到的模拟结果是逆时针螺旋，而Tsuboi等[7]使用基元反应模型并设置了不对称扰动，得到了逆时针旋转的结果。

图6 两种螺旋模式下三波线运动方式示意图Fig.6 Sketch of motion of triple point lines in two kinds of spinning mode

图7 两种螺旋模式下历史压力极值等值面Fig.7 Iso-surfaces of maximum pressure histories in two kinds of spinning modes

本文的模拟结果显示，只要设置了图2(a)所示直角模式的扰动，不管截面尺寸和网格密度多少，模拟结果均为逆时针螺旋；而设置图2(b)所示的对角扰动则一定会产生顺时针螺旋。

以上结果表明，不同的扰动形式的确对旋转方向产生了影响，且同一扰动形式在不同截面尺寸或者其他初始条件变化情况下只会产生一种旋转方向，不具有随机性。

为了验证改进CE/SE算法和Sichel二步模型的计算效果，把本文计算的胞格结构和前人的工作进行了对比，如图8、图9所示。可以看到对于直角和对角模式来说，模拟结果能够与实验很好的吻合；对于螺旋模式来说，数值模拟得到的爆轰波结构与其他高精度数值格式相差不大。

图8 不同数值模拟方法计算方管中对角模式和直角模式胞格结构与实验图样的比较Fig.8 Comparison of cellular patterns in diagonal or rectangular mode of square ducts using different numerical methods with experimental results

图9 不同数值模拟方法计算方管中螺旋模式胞格结构的比较Fig.9 Comparison of cellular patterns in spinning mode of square ducts using different numerical methods

一般认为，化学反应模型决定了胞格结构的形状和特征尺度，数值模型决定了胞格图案的精细程度和对比度。比较的结果表明，使用Sichel二步模型计算得到的胞格可以和基元反应模型相媲美，略优于一步模型；使用改进CE/SE格式得到的胞格结构细节清晰，不逊色于高阶精度的WENO格式。而使用改进CE/SE格式和Sichel二步模型所花费的计算资源却相当少，一般1 000万三维网格配置和5 000个时间步的方管算例用普通的4核CPU计算，在一周内即可得到完整结果。

4.3 临界情况结构变化

在临界情况算例1-2中，截面尺寸为2 mm，在计算区域前半部分，爆轰波仍然具有一个横向胞格，然而此时爆轰波结构处于不稳定的状态，胞格形状会出现一定的变形。经过一段较短的转化区之后，爆轰波稳定传播，此时横波扫掠前导激波形成的纺锤体沿xy,xz平面被剖分成1/4，投影在壁面上显示为半胞结构。

与典型的对角模式胞格结构相比，此时前导激波波阵面上三波线的数量减少为一组4条，形成一个封闭的长方形，如图10所示。可以想见，过小的截面尺寸压迫爆轰波横向结构，使得两组横波的相位差逐渐缩小，直至合并成一组横波，形成在这个截面尺寸下更为稳定的传播结构。

和算例1-2类似，算例2-2也接近转化为螺旋模式的临界情况，此时直角模式下并不存在如图10所示的半胞结构，而需要经过一个更长的转化区。在此种情况下，一开始爆轰胞格图样按照初始扰动形式产生一个横向胞格。接下来两组三波线会逐渐在计算区域中段累积π/8弧度的相差。如图11所示，三波线的运动模式与算例1-4中看到的情形类似，但是两组三波线交汇形成的封闭图样是长方形而不是正方形，这是π/8相差产生的直观结果。另外考察图11中yz截面历史压力极值的分布，可以清楚地看到4个压力集中的点(三波点)螺旋式地前进，这种波阵面运动模式就是图6中4个单头螺旋以不同相位的组合，因此可以称这种胞格传播模式为四头螺旋模式。进一步观察图4(b)中截面尺寸为2 mm的xy壁面胞格结构(即历史压力极值分布)可以看到,与一般直角模式相比，四头螺旋的拍波由于相位差不同,并不会出现在鱼鳞状胞格结构的顶点连线附近,而是会出现在顶点连线和中心汇聚点的中间位置。

图10 算例1-2中一个周期内压力等值面和三波线的运动Fig.10 Pressure iso-surfaces and motion of triple point lines in one period in Case 1-2

图11 过渡区间压力等值面演化和三波线运动以及yz截面历史压力极值变化(D=2 mm，初始直角扰动)Fig.11 Pressure iso-surfaces evolution and motion of triple point lines as well as variation of maximum pressure histories on yz sections in transition zone (D=2 mm, initial rectangular perturbation)

在Hanana等[1]的实验中可以得到这种非同相(Partially out of phase)的直角模式。如图12所示，利用烟熏法得到的非同相管壁胞格图样中，垂直管壁的亮条纹即数值模拟中的拍波，此时亮条纹位于相邻两个横波交汇点的中间区域，与算例2-2中四头螺旋模式下的胞格结构十分类似，进一步验证了计算结果的合理性。

图12 Hanana[1]实验中不同相的实验结果Fig.12 One of typical soot records with partially out of phase in Hanana’s experiments[1]

当然，四头螺旋结构也只是计算区域中段的过渡结构，最终处于平行状态的两组横波会逐渐缩小相位差乃至合并成一组，形成如图6所示的单头螺旋结构。

为了进一步比较直角模式和对角模式的稳定性，分析临界尺寸时波阵面附近压力脉冲极值的变化与爆轰波结构变化的关系，本文提取了临界情况算例历史压力极值在中心线(y= 1 mm,z= 1 mm)处沿着x方向的分布图，如图13所示。在起爆阶段，两种传播模式受初始扰动影响，都暂时形成一个横向胞格的对角模式和直角模式。在转化区，两种模式的爆轰波都会出现中间转换结构，如前所述，对角模式下爆轰波由一个横向胞格逐渐转变为半胞结构。虽然胞格结构的转化区很短，但是按照压力脉冲幅度的变化来看，在很长一段区域内每个周期的压力振幅和峰值并不稳定。在对角模式下的过渡结构中压力脉冲峰值的振荡出现不规则的涨落，而在直角模式下则呈现振荡幅度不断下降的趋势，直到两种模式达到新的稳定结构。因此从这个角度来讲，对角模式在此种尺寸下会转变为半胞结构是合理的。另一方面，在直角模式下，可以发现压力历史的包络线呈现出一个减小的趋势，直到丧失稳定性。如前所述，此区域内直角模式胞格图样会逐渐转变为四头螺旋结构。最终稳定区域两种模式的压力脉冲极值都形成等幅振荡，这意味着爆轰波结构形成自持稳定。对角模式的稳定结构是半胞结构，而直角模式在稳定区形成单头螺旋爆轰，此时三波线汇聚成点沿着壁面做螺旋运动，中心线附近的历史压力极值是很小的。

图13 两种传播模式历史压力极值沿着x方向中心线的比较(D=2 mm)Fig.13 Comparison of maximum pressure histories along central lines in x-axis direction between two kinds of propagation modes (D=2 mm)

从结果上来说，对角模式胞格结构比直角模式更为稳定，前者三波线累计相位差后仍然可以保持结构的稳定性，后者累计相位差后容易产生中间态的螺旋结构，并最终转变为单头螺旋结构。