基于改进区间值直觉模糊熵的投资方案优选
2019-05-23江晓珍
江晓珍
(福州外语外贸学院 经管学院, 福州 350202)
自从Zadeh[1]教授提出直觉模糊集理论之后,对其研究就没有停止过。熵理论始终是模糊理论研究的一个热点,熵也被广泛应用在模糊集理论中。熵是一种用来表征系统紊乱程度的度量,最早在热力学中用来表示物质的状态,在化学中也被广泛应用。Zadeh[1]教授将熵的概念引入模糊集(FS)中,对熵进行定义,用来度量模糊集的不确定性程度或模糊程度。熵值越大,模糊集越模糊;熵值越小,模糊集越清晰。熵被广泛应用在多属性决策中,通过熵权法的转换后可用于确定属性权重或专家权重。此后,有学者专门研究如何度量模糊集的熵,Luca和Termini[2]给出了构建模糊集熵的公理化条件。自从Atanassov[3]在Zadeh教授所定义的模糊集的基础上定义了直觉模糊集(IFS)之后,研究直觉模糊集的不确定性程度成为一个重要的课题。Szmidt 和Kacprzyk[4]将Luca和Termini提出的模糊集公理化条件扩展到直觉模糊集,给出了构建直觉模糊集熵的公理化条件。Burillo and Bustince[4]提出了另外的直觉模糊集的公理化条件。模糊熵只考虑隶属度和非隶属度对熵的影响,而直觉模糊熵既考虑隶属度和非隶属度对熵的影响,又考虑根犹豫度对直觉模糊熵的影响。因此,相对于模糊熵而言,直觉模糊熵更具合理性和可行性。据这些公理化条件,许多学者取得了不少成果,定义了各种不同的熵。例如:魏翠萍等[6]基于三角函数构建了直觉模糊熵;刘满凤等[7]用余弦函数构建了直觉模糊熵;尹胜等[8]定义了指数形式的改进直觉模糊熵,并扩展到区间值直觉模糊环境;熊升华等[9]在对数函数的基础上定义了广义的直觉模糊熵,考虑了决策者的风险态度;Mao等[10]认为直觉模糊熵由直觉信息(犹豫度)和模糊信息(隶属度和非隶属度之差的绝对值)构成。Szmidt 和Kacprzyk考虑了模糊信息而忽略了直觉信息,Burillo 和 Bustince考虑了直觉信息而忽略了模糊信息,因此这两个公理化条件都有其不足之处,据此提出了改进的直觉模糊熵公理化条件并构建包含直觉信息和模糊信息的直觉模糊熵。高明美等[11]针对Szmidt 和 Kacprzyk以及Burillo 和 Bustince的缺陷提出新的公理化条件,构建了比较合理的直觉模糊熵。Zhu等[12]也定义了与文献[11]相同的公理化条件。此外,Szmidt 和 Kacprzyk从直觉模糊集所包含的信息量的角度定义了信息量μ+υ和可靠度|μ-υ|,该理论与Mao等[10]提出的直觉信息和模糊信息的理论一致,可用于直觉模糊熵和区间值直觉模糊熵的构建。
Atanassov 和 Gargov[14]将直觉模糊集扩展到区间值直觉模糊集,使得人们能更好地对模糊问题进行处理。也有不少学者对区间值直觉模糊熵进行了研究。Wei等[15]将直觉模糊集拓展到区间值直觉模糊集,并给出了区间值直觉模糊熵公式。Jin等[16]使用连续有序加权集结算子(COWA)构造了区间值直觉模糊连续熵。高明美等[17]将改进的直觉模糊熵公理化条件拓展到区间值直觉模糊熵,给出了区间值直觉模糊集的新的熵。Zhao等[18]基于MULTIMOORA定义了连续加权型区间值直觉模糊熵。
虽然高明美等[11]根据新的公理化条件构建了新的熵,但该熵不能区分隶属度为0.5或非隶属度为0.5时的直觉模糊熵,同样的情况也存在于文献[11]构建的区间值直觉模糊熵中。文献[6-8]不能将隶属度和非隶属度相等的直觉模糊熵区分开来。同样,文献[15-17]也不能将隶属度和非隶属度相等的区间值直觉模糊熵区分开来。为了克服上述缺陷,本文基于高明美等[11]和Zhu等[12]定义的公理化条件,考虑直觉信息(信息缺乏)和模糊信息(信任缺乏)的情况构建新的直觉模糊熵和区间值直觉模糊熵。最后,将新的区间值直觉模糊熵应用于投资方案优选。
1 基本知识
下面给出直觉模糊集的一些基本概念。

A={

对于任意的A,B∈IFSs(X),∀x∈X,它们之间的关系为:
1)A⊆B当且仅当μA(x)≤μB(x),υA(x)≥υB(x);
2)A=B当且仅当A⊆B,A⊇B;
3)A的补集AC={




为计算直觉模糊集A和B之间的距离,可采用以下的直觉模糊集汉明距离公式[20]进行计算:
直觉模糊熵的构建必须满足一定的公理化条件,本文根据高明美等[11]和Zhu等[12]提出的下列直觉模糊熵的公理化条件构建改进的直觉模糊熵:
(P1)E(A)=0,当且仅当A是一个清晰集;
(P2)E(A)=1⟺μA(x)=0,υA(x)=0;
(P3)E(A)=E(Ac);
(P4) 对于任意的A,B⊆IFSs,x∈X,E(A)≤E(B),如果A是B的锐化集,即A⊆B,μB(x)≤υB(x)或A⊇B,μB(x)≥υB(x);
(P5) 当πA(x)=πB(x),|μA(x)-υA(x)|≥|μB(x) -υB(x)|时或当|μA(x)-υA(x)|= |μB(x)-υB(x)|,πA(x)≤πB(x) 时,E(A)≤E(B)。
其中:|μA(x)-υA(x)| 为模糊信息;πA(x)为直觉信息[10]。
此外,区间值直觉模糊熵的构建也必须满足一定的公理化条件,本文根据高明美等[17]给出的下列区间值直觉模糊熵的公理化条件构建改进的区间值之间模糊熵:
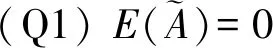

2 改进的直觉模糊熵
2.1 改进的直觉模糊熵
根据文献[11-12]定义的新直觉模糊公理化条件,考虑直觉信息和模糊信息对熵的影响,Szmidt和Kacprzyk[4]从信息量的角度,把μ+υ定义为直觉模糊集所含的信息量的大小,因此犹豫度πA(x)=1-μA(x)-υA(x)可以理解为信息量的缺乏,它同时也是直觉信息。文献[13]定义了可靠性|μ-υ|,它也是模糊信息,1-|μ-υ|可以理解为可靠性的缺乏。根据这两个理论,在同时考虑直觉信息(信息的缺乏)和模糊信息(可靠性的缺乏)的情况下,使用对数函数定义新的直觉模糊熵。
定义2对于任意的直觉模糊集A∈IFSs(X),∀x∈X,其熵为:
(1)
其中:1-|μA(x)-υA(x)|为可靠性的缺乏程度;πA(x)为信息量的缺乏程度;e为自然对数底数。
定理1式(1)定义的熵E(A)是一个直觉模糊熵。
证明式(1)满足公理化条件(P1)到(P5),则E(A)是直觉模糊熵。
(P1) 若A={
反之,若E(A)=0,则1-|μA(x)-υA(x)|=0或πA(xi)·(1-|μA(xi)-υA(xi)|)+e-1=1,因为0≤1-|μA(x)-υA(x)|≤1,0≤πA(xi)≤1,0
(P2) 若A={
反之,若E(A)=1,因为存在0≤1-|μA(x)-υA(x)|≤1,0≤πA(xi)≤1,0
(P3) 从A和其补集AC的关系可知该条件成立。证明过程略。
(P4) 令E(A)=f(x,y),考虑函数
f(x,y)=(1-x)ln(xy+e-1)
其中:x=|μA(x)-υA(x)|;y=πA(xi),0≤x,y≤1。对x求偏导,得
因此,E(A)随|μA(x)-υA(x)|的增大而减小,随|μA(x)-υA(x)|的减小而增大。
下面分两种情况进行讨论。


(P5)从(P4)的证明中可知E(A)随|μA(x)-υA(x)|的增大而减小,随|μA(x)-υA(x)|的减小而增大,因此当πA(x)=πB(x),|μA(x)-υA(x)|≥|μB(x)-υB(x)|时,E(A)≤E(B)。
与(P4)一样,令E(A)=f(x,y),考虑函数
f(x,y)=(1-x)ln(xy+e-1)
其中:x=|μA(x)-υA(x)|;y=πA(xi),0≤x,y≤1。对y求偏导,得
可见,E(A)随πA(x)的增大而增大,随πA(x)的减小而减小。
由此,当 |μA(x)-υA(x)|=|μB(x)-υB(x)|,πA(x)≤πB(x) 时,E(A)≤E(B)。
从上述的证明可知:式(1)定义的熵E(A)是一个直觉模糊熵。
2.2 与现有直觉模糊熵的比较
为体现本文中所提出的改进区间值直觉模糊熵的优越性,有必要将其与已有的部分直觉模糊熵进行比较。
从上述的文献综述中可以看到:很多学者根据直觉模糊熵公理化条件给出了各种不同的熵。Szmidt和Kacprzyk[4]给出的熵为ESK(A),Burillo and Bustince[4]提出直觉模糊熵为EBB(A),魏翠萍等[6]构建的熵为EWCP(A),刘满凤等[7]用余弦函数构建了直觉模糊熵为ELMF(A),当p=q=1时,熊升华等[9]构建的熵为EXSH(A),高明美等[11]提出的新直觉模糊熵为EGMM(A),分别如下:
当有5个直觉模糊集:
A1={〈x,0.5,0.5〉|x∈X};A2={〈x,0.3,0.3〉|x∈X};A3={〈x,0,0〉|x∈X}
A4={〈x,0.5,0.3〉|x∈X};A5={〈x,0.7,0.1〉|x∈X}
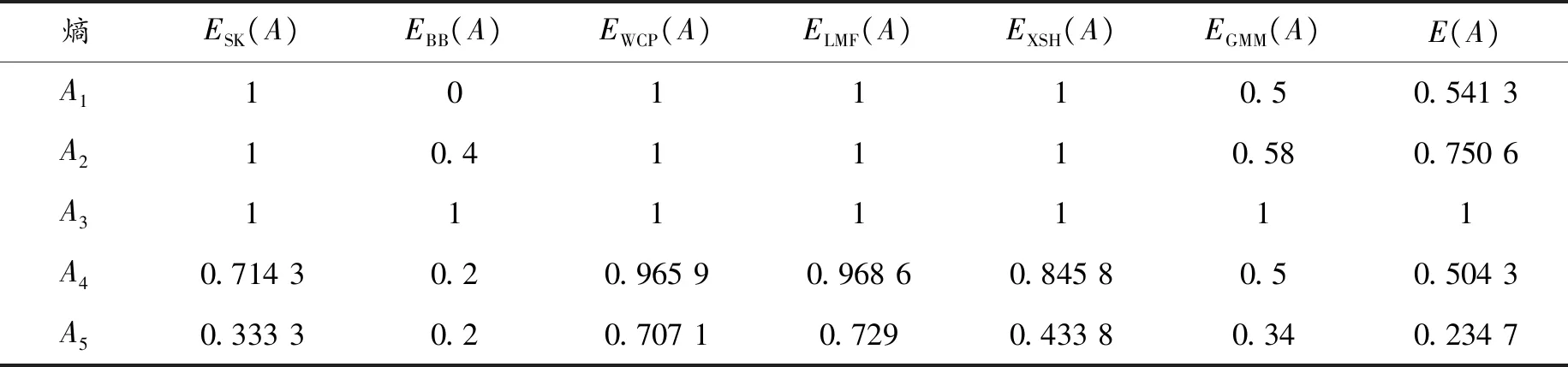
采用上述6个不同的直觉模糊熵公式与本文提出的直觉模糊熵公式计算A1-A5的熵,所得结果在表1中列出,以方便比较。
从表1中可以看出:ESK(A)、EWCP(A)、ELMF(A)和EXSH(A)不能区分A1、A2和A3。当μA(x)=υA(x)时,ESK(A)、EWCP(A)、ELMF(A)和EXSH(A)都不能将其区分开来。EBB(A)不能区A4和A5。EGMM(A)不能区分A1和A4。通过计算可知,EGMM(A)不能区分〈0.5,0〉和〈0.5,0.5〉连线上的直觉模糊集的熵,也不能区分〈0,0.5〉和〈0.5,0.5〉连线上的直觉模糊集的熵。本文提出的直觉模糊熵E(A)能将所有的直觉模糊集的熵区分开来,因此可以看出:与上述6个直觉模糊熵相比较而言,本文提出的熵E(A)更加合理。
表1 不同直觉模糊熵下的计算结果
熵ESK(A)EBB(A)EWCP(A)ELMF(A)EXSH(A)EGMM(A)E(A)A1101110.50.541 3A210.41110.580.750 6A31111111A40.714 30.20.965 90.968 60.845 80.50.504 3A50.333 30.20.707 10.7290.433 80.340.234 7
3 改进的区间值直觉模糊熵
3.1 改进的区间值直觉模糊熵
将式(1)构建的直觉模糊熵扩展到区间直觉模糊集,得到新的区间值直觉模糊集。

(2)
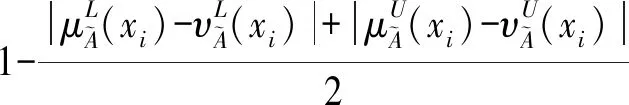


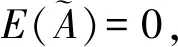
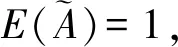
f(x,y)=(1-x)ln(xy+e-1)

下面分两种情况进行讨论。
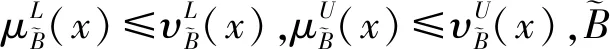
因此,E(A)≤E(B)。

因此,E(A)≤E(B)。
求函数
f(x,y)=(1-x)ln(xy+e-1)
关于y的1阶偏导,有

图1 直觉模糊熵

3.2 与现有区间值直觉模糊熵的比较
为体现本文中提出的改进区间值直觉模糊熵的优越性,有必要将其与已有的部分区间值直觉模糊熵进行比较。

现有6个区间值直觉模糊集:
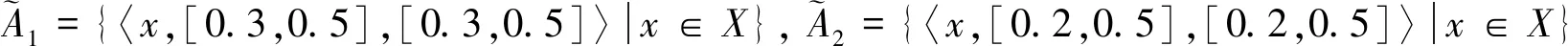

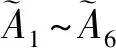

表2 不同区间值直觉模糊熵下的计算结果
4 投资方案选择


表3 方案评价矩阵
1) 用式(2)计算得到区间值直觉模糊熵矩阵,如表 4所示。
3) 用下面的算术平均加权集结算子[17]
对方案的各属性进行集结,得到

4) 用文献[17]给出的得分函数
计算得到各方案的得分值为:
5) 得分值越大,方案越优,因此各方案的排序为:

表4 区间值直觉模糊熵矩阵

C1C2C3C4A10.584 90.298 90.576 90.323 5A20.597 90.298 90.576 90.323 5A30.589 90.696 50.225 70.340 1A40.559 20.345 40.433 80.225 7
5 结论
根据新的公理化条件,在考虑直觉信息(信息缺乏)和模糊信息(信任缺乏)的情况下,使用对数函数,定义了新的改进的直觉模糊熵和区间值直觉模糊熵,通过证明可知新的改进的直觉模糊熵满足直觉模糊熵公理化条件,区间值直觉模糊熵满足区间值直觉模糊熵的公理化条件。此外,与现有的直觉模糊熵和区间值直觉模糊熵进行比较可知:① 在犹豫度相同时,可通过隶属度和非隶属度之差来区分不同的熵;② 在隶属度和非隶属度之差相同时,通过犹豫度区分不同的熵;③ 最模糊的直觉模糊集是〈0,0,1〉;④ 新的区间值直觉模糊熵具有新直觉模糊熵的优点;⑤ 也克服了文献[17]存在的缺陷。因此,新熵具有一定的合理性和可行性。通过投资案例的应用和比较,可知主观赋权法和客观赋权法对投资方案的优选产生重要的影响。新定义的熵给决策者提供了更加精确的客观赋权方法。
