带随机扰动的耦合谐振子网络系统的同步

杨 伟，张 华,2，叶志勇，武晓慧，韩宝如

(1.重庆理工大学 理学院， 重庆 400054; 2.铜仁学院 大数据学院， 贵州 铜仁 554300；3.重庆医科大学 医学信息学院， 重庆 400016)

自然界中有很多生物群体会自发呈现出规律一致性的运动现象，例如：鱼群能快速一致地改变队形来应对猎物的追捕，萤火虫能节奏一致地进行闪烁，蚂蚁遵循一些简单的规则就能进行觅食等复杂群集动力学同步行为[1]。在过去几十年中，复杂网络系统的同步一致性研究受到了该领域众多国内外学者的广泛关注，得到了很多重要的研究成果[2-8]。一般来讲，同步是指含有两个或两个以上子系统的网络在一定时间内，其运动状态趋于一致的动力学行为[4]，主要有有限时间同步[5]、几乎处处同步[6]，分群同步或时间无穷大时同步[7-8]等。

在复杂动力网络系统的同步研究中，子系统为谐振子的一类二阶多智能体网络系统的同步问题，在过去10年中一直是国际上的一个研究热点，国内外学者在多种约束条件下给出了许多重要的控制输入协议[9-14]。例如，Ren W首次在有向网络拓扑结构下建立了基于局部耦合的时间连续型谐振子网络系统的模型，给出了该连续型耦合谐振子网络系统的同步态以及达到同步的判定条件[10]。随后，Ballard等针对时间离散型谐振子网络系统进行建模并设计了一个简单的分布式控制输入算法，并研究将该模型应用于机器人的同步协调运动问题，利用离散时间分布耦合谐振子设计了对称编队的控制策略，给出了网络化移动机器人协调运动的物理实验[11]。

最近，Zhang等[12-13]在系统无法感知振子之间的相对速度状态而只能在一系列离散时刻获得相对位移状态的约束条件下，提出了基于相对位移采样信息的两种分布式控制输入协议：脉冲控制协议和采样控制协议。分别在无向固定拓扑结构、无循环划分的分簇拓扑结构下，给出了系统达到同步的一些充分必要条件，得到了系统在达到同步时采样周期与系统的自身参数以及拓扑结构之间的准确函数关系。随后，Wan等[14]在基于离散时刻相对速度的耦合情形下，分析了网络型谐振子系统的分群同步现象并给出了谐振子网络系统达到同步的一些判定准则。

值得注意的是以上几乎所有的工作都是建立在非随机耦合的谐振子系统上的。但是，在现实世界中由于测量噪声的不可避免性，系统均不同程度地受到各种噪声的干扰。因此，在随机噪声环境下研究耦合谐振子网络系统的同步问题具有重要的实际意义。例如，Shang等[15]基于随机时滞微分方程的稳定性理论、代数图论和矩阵论研究了带有随机噪声和时滞的耦合谐振子系统的领导—跟随同步线性。Sun等[16]在无引导者的结构下，研究了随机噪声作用下耦合谐振子系统的同步，设计了两种分布式控制算法，得到了使耦合谐振子系统达到几乎处处同步的充分条件。但是，他们考虑的随机谐振子系统的漂移项和扩散项都是基于相对速度的耦合设计。

基于以上研究工作，考虑到实际工程中获知相对速度信息比相对位移信息更加困难这一现实，设计了一种由带有随机噪声的相对位移信息构成的分布式控制输入协议，并且得到了该网络系统达到几乎处处同步的一个充分条件。

1 基础知识和模型建立

1.1 符号说明

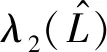
1.2 代数图论

代数图论是分析网络问题的重要基础。令G=(V,E,A)是一个n(n≥2)阶加权有向图，V={1,2,…,n}是有向图G的节点集合，Ni={j∈V∶(i,j)∈E}表示节点i的邻居集合，E⊂V×V是有向边界集，A=[aij]∈Rn×n是邻接矩阵。(i,j)∈E当且仅当aij>0(i≠j)，即节点i能够从节点j收到信息，(i,j)∉E当且仅当aij=0(i≠j)，即节点i不能够从节点j收到信息。

1.3 模型描述

耦合谐振子网络系统一般动力学方程为[18]：

(1)

其中：xi(t),vi(t)∈R分别表示第i个振子的位移和速度；α>0表示位移增益；ui(t)是分布式控制输入协议。

Sun等[16]提出了如下带有随机扰动的分布式控制协议：

(2)

其中：c>0表示耦合强度；aij表示振子i和振子j的相互作用。

值得注意的是，该协议中的控制输入项是由相对速度状态信息构成的，但是在现实中由于技术条件的限制，准确地测量相对速度要比测量相对位移困难。因此，本文给出如下基于带随机扰动相对位移状态的分布式控制输入协议：

(3)

其中：δ是噪声强度；B(t)是一个定义在完备概率空间(Ω,F,P)上的一维布朗运动，满足如下条件：E[dB(t)]=0，[dB(t)]2=dt。

研究目标是构建带有分布式控制算法(3)的耦合谐振子网络系统(1)达到几乎处处同步的充分条件。首先介绍如下著名的伊藤(It)公式。考虑一个n维随机微分方程

dx(t)=f(t,x(t))dt+g(t,x(t))dB(t)

(4)

其中，t≥0，x(t)∈Rn是状态向量，B(t)是一个m维独立标准的维纳过程，向量值函数f:[0,+∞]×Rn→Rn，g:[0,+∞]×Rn→Rn×m，并且f(t,0)=0，g(t,0)=0。

假设C2,1(Rn×R+;R)表示非负函数V(x,t)在Rn×R+上关于x二阶可导，关于t一阶可导。对于每一个V∈C2,1(Rn×R+;R)，定义从Rn×R+到R的极小生成元lV[19]

lV=Vt(x,t)+Vx(x,t)f(x,t)+

(5)

其中

为了证明主要结果，引入以下定义和引理。

定义1图G=(V,E,A)的节点i是平衡的当且仅当节点i的入度和出度相等，即degin(i)=degout(i)。有向图G是平衡的当且仅当它的所有节点均是平衡的。

degout(i)=Dii

(6)

2 主要结果

在分布式控制协议(3)下，网络型耦合谐振子系统(1)动力学方程写成矩阵的形式：

(7)

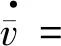
(8)

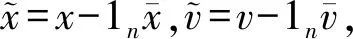
(9)

再令

那么方程(9)能写成以下形式：

de(t)=He(t)dt-δEe(t)dB(t)

(10)

(11)

证明首先构造一个正定的Lyapunov函数V(t)=eT(t)e(t)。通过伊藤(It)公式，能够计算极小生成元

lV=2eT(t)He(t)+

2eT(t)He(t)+δ2trace(eT(t)ETEe(t))=

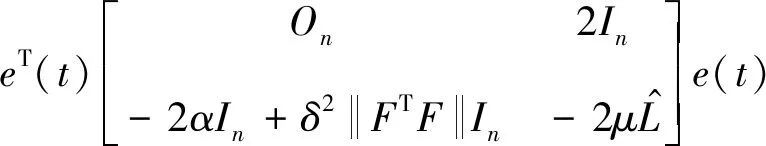
eT(t)Me(t)

矩阵M的特征方程是

即

(12)

要使得该特征方程的所有特征值为负数，则需满足

即

则对于所有的l=2,3，…,n，有

(13)

由于0=λ1<λ2≤…≤λn，那么只要

则矩阵M的所有特征值是负的。假设-λmin(M)是矩阵M的最大特征值，则

lV≤-λmin(M)eT(t)e(t)=-λmin(M)V(t)

(14)

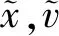
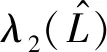
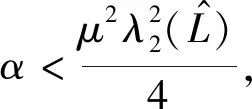
3 实验仿真

考虑由6个谐振子构成的网络系统，其网络拓扑结构以及边的权重如图1所示。

图1 系统网络拓扑结构

其对应的拉普拉斯矩阵为

根据定理1，如果7.737 2δ2<16<27.029 6+7.737 2δ2,即δ2<2.067 9，那么带随机扰动的网络型耦合谐振子系统(7)能够达到几乎处处同步。取δ=0.8，选择初始值为x1(0)=11，x2(0)=1，x3(0)=22，x4(0)=-5，x5(0)=-13，x6(0)=5，v1(0)=4，v2(0)=13，v3(0)=-15，v4(0)=2，v5(0)=-5，v6(0)=18。图2展示了系统随着时间的演化，位移xi(i=1,2,…,6)的变化曲线。图3展示了随着时间的演化，速度vi(i=1,2,…,6)的变化曲线。可以看出：随着时间的演化，各个节点的位移和速度均能够达到几乎处处同步。

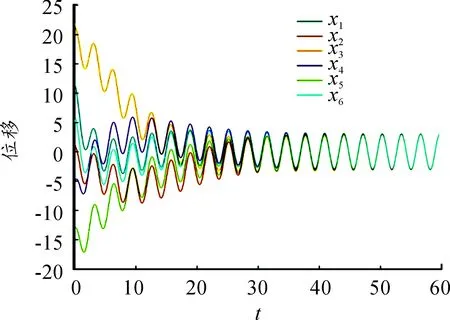
图2 位移状态时间反应曲线

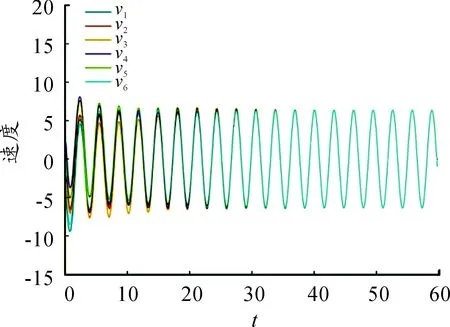
图3 速度状态的时间反应曲线

4 结束语

本文研究了在随机噪声扰动环境下网络型谐振子系统的几乎处处同步的问题。因实际操作中准确地直接测量振子的相对速度难于相对位置信息，因而设计了一种用准确的相对速度耦合信息和带随机噪声的相对位移耦合信息两部分构成的分布式控制输入协议。利用伊藤(It)公式以及拉普拉斯矩阵的谱理论，给出了随机耦合谐振子网络系统达到几乎处处同步的充分条件。数值模拟进一步验证了所提出结果的正确性和协议的有效性。在后续的研究计划中，我们将探索只含有相对位移耦合的随机耦合谐振子网络系统达到同步稳定的判定条件，以及带有通讯和输入时滞、噪声强度是如何影响随机耦合谐振子系统同步的机理等。