基于遗传算法的大数据资源分配算法
2019-05-23蔡柳萍
蔡柳萍,俞 龙
(1.广东技术师范学院天河学院 计算机科学与工程学院, 广州 510540;2.华南农业大学 电子工程学院, 广州 510642)
云计算将服务器端的物理资源通过虚拟化技术模拟为若干个独立且互不干扰的虚拟服务器[1],从而满足用户的资源请求。云计算为用户提供了安全、可靠的计算能力与存储容量,成为了许多网络应用的首选[2]。云计算的资源分配[3]主要分为2个阶段,其中第1个阶段按照用户任务所需的计算能力、存储容量、内存大小、网络带宽等资源将任务分配到合适的虚拟机;第2阶段将不同的虚拟机分配到合适的物理服务器,一个物理服务器可以容纳多个虚拟机[4]。目前,服务器管理虚拟机的工具主要有Xen与KVN等虚拟机管理软件。虽然云计算提高了物理服务器的利用率,有效降低了硬件成本与管理成本,但是各个应用程序与任务之间竞争共享资源池的资源为云计算资源的合理分配带来了新的难题[5]。
许多研究人员将云计算的资源分配问题建模为经典的多维装箱问题[6],问题的每个维度对应一种资源类型,例如CPU资源、内存资源、磁盘资源、带宽资源等。当前的云计算资源分配研究主要有几个目标,包括提高资源利用率、提高能量效率与实现负载均衡等[7-9]。本文的研究重点是提高云计算资源分配算法的资源利用率。
在提高资源利用率的算法中,文献[10]设计了以任务完成时间较短且成本最低为约束条件的调度模型。该资源分配算法能有效地兼顾完成时间和成本,在缩短任务完成时间的同时保证成本最小,提高了资源利用率。文献[11]设计了虚拟化的异构云计算体系结构,并提出了该体系结构下基于占优资源的多资源联合公平分配算法。该算法获得了更高的系统资源利用率,使需求与供给更加匹配,进而使用户获取更多的占优资源,提高了服务质量。文献[12]提出一种基于蚁群优化算法的任务调度方法,结合排序蚂蚁系统和最大最小蚂蚁系统的设计思想完成信息素更新,有效地提高了云资源的利用率。文献[6,11-12]通过优化算法搜索资源分配的最优解,该类算法一般将资源利用率作为首要优化目标,将能量效率、带宽利用率等作为次要优化目标,通过兼顾多个性能指标获得理想的分配方案。
本文设计了一种云资源的贪婪分配算法,将资源利用率作为唯一的优化目标,最小化云计算物理服务器的数量,并最小化每个服务器的资源浪费量。本文将云计算的资源分配问题建模为文献[6]的多维装箱问题,采用遗传算法搜索最优的虚拟机顺序,设计了一种贪婪算法最小化物理服务器的数量与每个物理服务器的资源浪费量。
1 总体架构
1.1 多维装箱问题模型
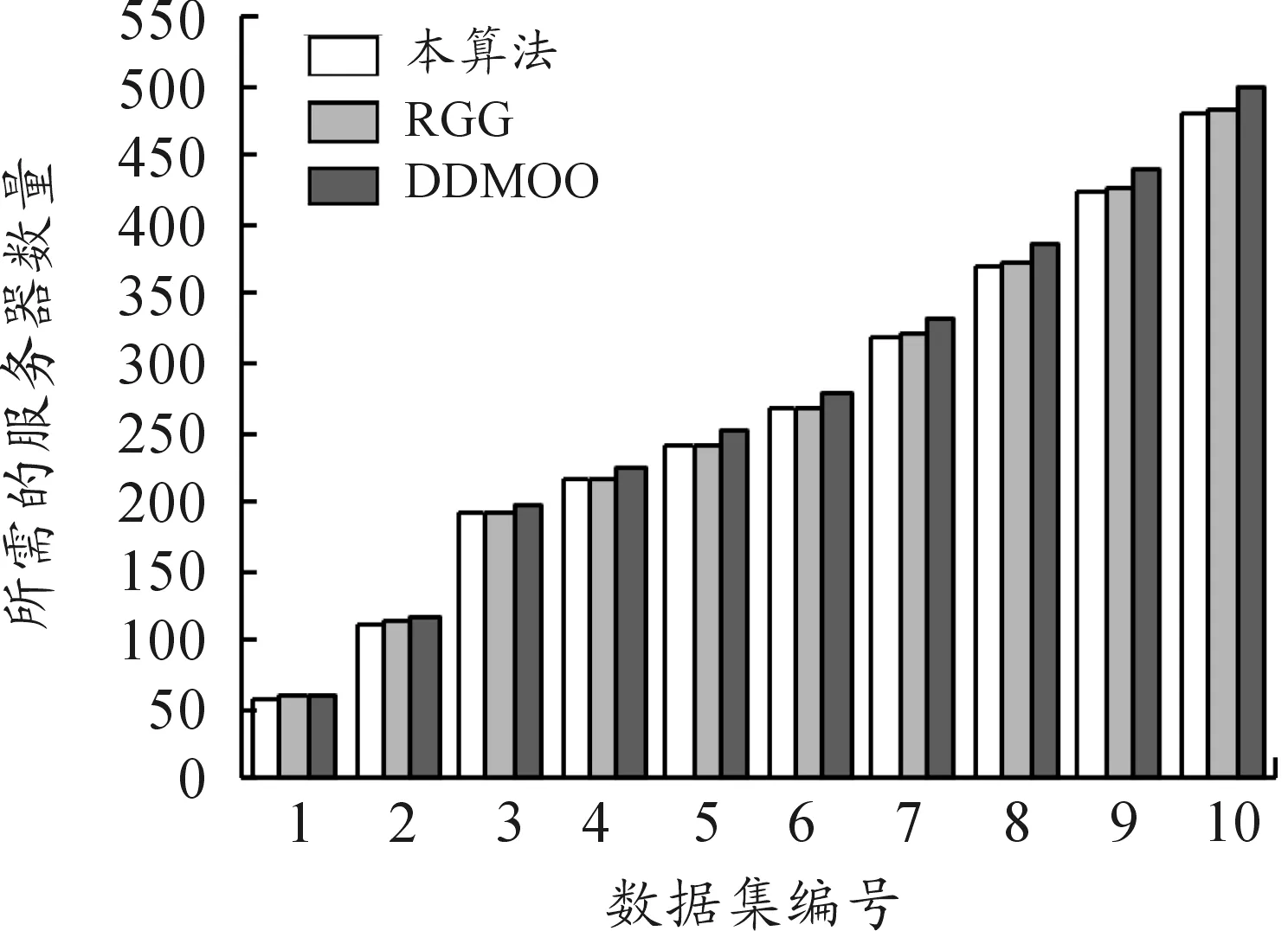
多维装箱问题描述为如下模型[6]:假设1个集合B包含m个相同的箱子,每个箱子各元素的容量表示为1个向量C=(C1,C2,…,Cd)。假设1个包含n个项的集合为L={X1,X2,X3,…,Xn},L的各项是需要装箱的元素,将各项表示为包含d个元素的向量Xj={Xj,1,Xj,2,Xj,3,…,Xj,d},式中Xj,k是第j项、第k个元素,其中0 将多维装箱问题的1个解表示为B={B1,B2,Bi,…,Bm},表示将n个项目装入m个箱子中,每个箱子可容纳S个项目。装箱的决策表示为Bi={X2,i,X7,i,X5,i,…,X5,i},约束条件为: (1) (2) ∀B,XBi+Xj≤C (3) 约束(1)说明每个项目必须装进1个箱子中,约束(2)说明每个维度中需求的项目不应超过箱子的容量,约束(3)说明将1个新项目装入1个箱子中,不应超过箱子的总容量。多维装箱问题是NP-hard问题[9],因此云计算资源分配问题的计算成本极大,本文设计了启发式贪婪算法来实现理想的计算成本。 首先对云计算资源分配问题做以下假设: 假设1每个任务均为用户预定义,即仅考虑静态的云计算资源分配情况。 假设2每个任务仅可分配到1个虚拟机中。 假设3每个任务请求定量的CPU与内存资源,即属于静态的调度问题。为了便于描述,仅考虑CPU与内存两个资源。 假设4云端均为相同的物理服务器。 假设5每个虚拟机仅能分配至1个服务器。 基于上述5点假设,将云数据中心的多维虚拟机部署问题建模为一个多维装箱问题。任务的数量决定了向量的元素数量,即需要装箱的项目数量。图1描述了将资源分配与虚拟机部署问题转化为一个二维向量的装箱问题。在第1阶段将请求所需的资源量(CPU与内存)映射至不同的虚拟机,在第2阶段将虚拟机部署至不同的可用物理服务器中。 图1 将资源分配与虚拟机部署问题转化为一个二维向量的装箱问题 假设云计算系统包含N个任务,对应N个虚拟机、M个服务器、R个资源,将不同的虚拟机装箱至一个物理服务器中。算法的目标是最小化所用物理服务器的数量(见式(4)),并最小化各个服务器的资源浪费量(见式(5)),问题的目标与约束条件建模为以下各式: 目标: (4) (5) (6) 约束条件为: (7) (8) (9) 式中:Wj,i(i∈[1,…,M],j∈[1,…,R])表示所有物理服务器的总资源浪费量;[SRCi,…,SRMi](i∈[1,…,M])表示第i个服务器的容量向量,SRC与SRM分别表示CPU资源与内存资源;[Ck,i,Mk,i](K∈[1,…,A],i∈[1,…,M])表示第k个虚拟机所需的CPU与内存;Pj,i∈[0,1](i∈[1,…,M],j∈[1,…,N])表示装箱的决策结果。式(5)表示资源分配的结果应当最小化所有服务器的资源浪费量。式(6)为计算资源浪费的方法。式(7)表示每个虚拟机仅被分配到一个服务器中。式(8)、(9)表示虚拟机的分配结果不能超过物理服务器的容量。 本文设计了一种改进的遗传算法,以提高遗传算法对装箱问题的求解效果。装箱问题的目标是最小化装载一组项目的箱子数量。首先,需要搜索一个项目排序的最优解,并且寻找向量装箱问题中项目需求之间的关系。 本算法分为3个主要的函数:init_VM函数、Resource_optimize函数与deploy_VM函数。init_VM函数根据输入的请求负载量初始化虚拟机;Resource_optimize函数生成虚拟机的部署决策,将一个启发式贪婪算法作为遗传算法的目标函数;deploy_VM函数按照装箱决策结果将虚拟机分配至云服务器中。 算法1 基于遗传算法的资源分配算法主程序1.初始化:J=0;VM=0;T=0; Optimized_Solution=NULL;//初始化任务数量、虚拟机数量、终端条件与最优解;2.建立一个描述文件,其中包含服务器数量、服务器容量、任务数量、每个任务所需的资源量;3.调用init_VM函数;4.调用Resource_optimize函数;5.调用deploy_VM函数 算法2 init_VM函数1.初始化VM;//初始化虚拟机2.WHILE J<任务数量;//描述文件3.J=J+1;4.根据任务需求为任务分配虚拟机;5.VM=VM+1算法3 Resource_optimize函数1.初始化终端条件与资源池大小;2.C_Length=VM;//染色体长度设为虚拟机数量3.WHILE (T < 终端条件)4.N=资源池大小;5.T=T+1;6.WHILE (N≠0)7.遍历每个服务器与虚拟机的需求,使用启发式贪婪算法、按照遗传算法搜索的最优虚拟机顺序将虚拟机分配至物理服务器;8.使用将染色体对应的虚拟机顺序转化为装箱解;9.使用适应度函数计算染色体适应度;10.N=N-1;11.Best_Solution=search_optimal_order(资源池);//搜索资源池的最优顺序12.FOREACH i FROM 1 TO(资源池大小/2);13.[染色体1,染色体2]=轮盘赌机制;14.[子代1,子代2]=crossover(染色体1,染色体2);15.save(新资源池,子代1,子代2);//将子代保存至新资源池内;16.资源池=新资源池;//更新当前的资源池算法4 deploy_VM函数IF((Optimized_Solution == NULL) || fitness(Optimized_Solution) 多维装箱问题是一个排序优化问题,遗传算法的染色体编码代表了虚拟机的顺序,每个染色体(一个数组)代表了序列中的一个位置。 每个染色体的长度等于需要装箱的虚拟机数量N,图2所示是染色体的结构实例。 图2 染色体编码实例 将染色体编码为N个整数的数组(一维阵列),染色体基因是一个虚拟机的序号,如图3所示。 图3 染色体与云计算资源的对应关系 将启发式贪婪装箱算法封装于遗传算法的适应度函数中。每个装箱解对应一个染色体,因此需要评估每个装箱解的性能。在目标函数中输入上述染色体,使用启发式贪婪算法根据输入的资源请求搜索最优的装箱解,目标函数的操作如下所示: 步骤1将虚拟机的实际需求与染色体顺序中的虚拟机匹配,该操作将一维数组形式的染色体转化为矩阵形式,矩阵的元素描述了请求所需的虚拟机资源。 步骤2使用装箱函数搜索装箱的顺序,装箱解的每个元素包含2个值,第1个值是装箱虚拟机的数量,第2个值是物理服务器的编号。图4所示是装箱解的编码格式。 图4 装箱问题解的编码格式 步骤3计算容纳给定虚拟机序列所需的物理服务器数量,计算各个服务器的资源浪费量。 目标函数为适应度函数提供了部分参数,例如服务器数量值。目标函数的输出结果为最优的装箱解与对应的染色体,决定了各个虚拟机分配至指定物理服务器的结果。 大多数基于遗传算法的云资源分配机制[13]使用启发式算法初始化云计算资源的资源池,然而,这些启发式算法导致染色体编码不充分,为遗传算法的交叉操作与交换操作带来了极大困难。本算法将启发式算法作为目标函数的一部分,将交换的染色体作为目标函数的输入参数,从而极大地降低了染色体编码与交叉操作的复杂度。本算法的目标是最小化物理服务器的总数量,建模为以下各式: f(O)=TS·Rtotal (10) Rtotal=RCPU+RMEM (12) (13) (14) 式中:f(O)是确定染色体顺序的染色体;TS是可用服务器的总数量;S是所需的物理服务器数量;Rtotal是服务器的总归一化剩余容量;RCPU表示归一化的CPU剩余容量,通过最小化每个服务器的剩余资源减少每个服务器的资源浪费量[14]。 选择策略从父代种群选出适应度较高的个体,生成后代种群,本算法采用轮盘赌选择策略。将种群的每个个体映射至轮盘的一片,其中轮盘片的大小与每个个体的适应度成正比关系F(i)。P(i)是染色体被选择的概率,P(i)与F′(i)成比例关系。P(i)定义如下: (15) F′(i)=1/F(i) (16) 遗传算法的交叉操作选择2个或多个父代染色体进行置换操作,生成新的子代。当前有许多染色体的交叉操作方法,例如顺序交叉、部分匹配交叉、位置交叉与单性交叉。本文测试了上述所有的交叉操作,顺序交叉与单性交叉获得了最优的效果,因此本文选择这两种交叉操作。 参考文献[16]设置了实验的遗传算法参数,如表1所示。C语言编程实现本算法,采用LibGA动态库(http://lancet.mit.edu/ga/)。LibGA是一个遗传算法的C语言编程开发库。操作系统为Ubuntu 14.04,硬件环境为Intel 酷睿i7 4770处理器,8 GB内存。 由于本算法的目标是优化云计算的资源利用率,因此直接将所需的服务器数量作为算法的性能评价指标。本文进行2组实验,第1组实验将本算法与其他多维装箱启发式算法比较,评估本算法对于多维装箱启发式算法的改进效果;第2组实验将本算法与其他云计算资源分配算法比较,评估本算法对于计算资源分配算法的改进效果。 表1 本算法的参数设置 本算法的目标是快速、高效地求解多维装箱问题。将本算法与两种多维装箱算法进行比较,两种算法分别为BONJRA[15]与MFFD[16]。MFFD是一种传统的启发式多维装箱问题求解算法,BONJRA是近年的一种性能较好的多维装箱问题求解算法。 图5所示是本算法、BONJRA[15]与MFFD[16]的结果比较,可清晰地看出本算法对于不同数量的虚拟机均实现了服务器数量最少。说明本算法适用于不同的问题规模,且优于其他两种多维装箱算法。 本文算法计算的服务器数量平均结果比MFFD与BONJRA分别减少了约34%与39%,与MFFD最大的差别在于本算法引入了改进的遗传算法。因此,可以说明本算法通过遗传算法提高了多维装箱算法的求解性能。 图5 3种算法分配的服务器数量 RGG[14]是另一种基于遗传算法的云计算资源分配算法,DDMOO[17]则是近年来性能表现优异的云计算资源分配算法。将本文算法与这两种算法进行比较,综合评估本算法对云计算资源的分配性能。实验采用文献[14]中10个不同规模的数据集。图6所示是本文算法、RGG与DDMOO 3种算法的计算结果。图6显示:数据集规模较小时,本算法、RGG与DDMOO的结果较为接近;随着数据集规模的增加,DDMOO算法的结果明显高于本算法,对于第10个数据集,DDMOO算法的服务器数量比本算法大约多40个,而RGG的服务器数量则比本算法多4个。可以看出,本文算法对于10个问题均优于RGG与DDMOO。 图6 3种云计算资源分配算法对文献[19]的10个数据集的实验结果 此外,RGG的适应度评估总次数为7 500,而本文算法的适应度评估总次数仅为1 700,适应度函数计算总次数比RGG减少约77.33%。因此,本文算法对不同规模的问题均可获得最优的资源分配结果,且具有较高的计算效率。 本文设计了一种云资源的贪婪分配算法,将资源利用率作为唯一的优化目标,最小化云计算物理服务器的数量,并最小化每个服务器的资源浪费量。本文将云计算的资源分配问题建模为文献的多维装箱问题,采用遗传算法搜索最优的虚拟机顺序,设计了一种贪婪算法最小化物理服务器的数量与每个物理服务器的资源浪费量。该算法存在的不足之处在于,遗传算法的迭代寻优程序对于大规模问题的计算时间较长,对计算机的处理能力有较高的要求。 未来将关注网络带宽、存储资源等更多维度资源分配的贪婪算法,提高云计算资源分配算法的计算效率。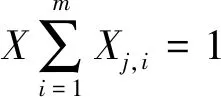

1.2 云计算资源分配的问题模型

2 遗传算法搜索最优的虚拟机顺序
2.1 算法设计


2.2 染色体编码


2.3 目标函数与适应函数
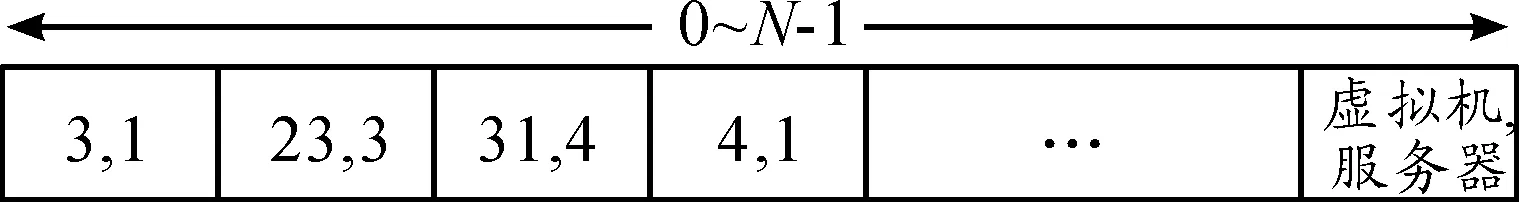
2.4 选择策略

2.5 交叉操作与变异操作
3 实验环境与参数设置

3.1 与其他多维装箱算法比较

3.2 与其他云计算资源分配算法比较
4 结束语
