破胶程度对压裂返排液水力旋流器内流场及分离效果的研究

王华健,周彤旭,孙伟华,王新龙,徐丽萍,肖小龙2,张 华3,刘 冰

(1.山东科技大学 机械电子工程学院，山东 青岛 266590；2.中石化石油工程设计有限公司，山东 东营 257026；3.山东莱克工程设计有限公司，山东 东营257026)

水力压裂技术在页岩气开采中的广泛应用推动了各国页岩气开发热潮，改变了全球能源供需格局[1-3]。然而在压裂过程中会产生大量的返排液，其具有大液量、大砂量、高黏度、高化学需氧量(chemical oxygen demand,COD)值、高含盐量等特性，处理不当将对环境产生污染[4-5]。处理压裂返排液的方法众多，传统处理方法主要有物理法(筛滤、吸附和气浮等)、化学法(中和法、氧化法、混凝法和微电解法)、生物法等[6]。由于单一的方法对压裂返排液的处理不彻底，从而不能达到回用或者排放的标准。因此将上述两种或者多种方法进行联合，实行模块化处理。随着技术的进步，出现了一些新型的压裂返排液处理技术，比如机械蒸汽再压缩蒸发技术、“智能海绵”吸附技术等。目前国内主要用联合工艺对页岩气压裂返排液进行模块化处理[7]。在压裂返排液联合处理工艺的旋流除砂模块主要是除去桥塞碎片，支撑剂，泥砂等大于50 μm的固体颗粒。为达到回注的要求，需要对10～50 μm的固体颗粒进行再次清除。在精细化过滤阶段，由于压裂返排液粘度较大加上破胶程度不高，采用过滤袋进行过滤的方式容易引起堵塞[8]。

水力旋流器由于结构简单、使用成本低、处理量大、分离效率高等优点而被应用于细小固体颗粒的清除[9]。水力旋流器发展至今，随着应用场合的不同种类也不尽相同。由于内部流场流动形式的复杂性，以及操作参数、物性参数和结构参数的不固定性，旋流器的设计并未形成统一的标准，从而不能形成通用的模型，现存大多数的设计方法也大多是根据经验所得，一般基于或者介于理论之间[10]。因此对某一特定旋流器的优化研究显得尤为重要。

本研究考察了压裂返排液在不同破胶程度下对水力旋流器分离效果的影响，通过CFD软件fluent和实验对旋流器内部流场的特征以及分离效率进行了定量研究，探讨破胶程度与流场稳定性、半自由涡区运动指数的变化趋势、能量损失、空气柱的大小和零速包络面的关系，并对外特性中的分离效率进行分析。通过对内流场及外特性的研究，得出两者之间的相互关系，并通过调节一些操作参数从而达到预期的分离效果，为不同破胶程度下压裂返排液的固液分离提供技术指导，以达到高效分离、减小能耗的目的。

1 模型

1.1 数学模型

由于水力旋流器内部流场的复杂性，模型的选择显得尤为重要。雷诺应力模型(Reynolds stress model，RSM)考虑了张力快速变化、流线型弯曲和旋涡，因此在三维流动方面有着较高的计算精度，并且通过大量的实验研究与模拟的对比分析得出雷诺应力方程，可以较为准确地模拟出水力旋流器的内流场，因此本研究选择雷诺应力模型为湍流模型[11]。

经量纲分析，整理后的RSM模型为：

(1)

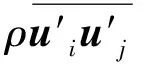
Mixture模型适合于有相混合或分离的情形，并且对于此模型的使用方法在其他的文献中有详细的记载，这里不再赘述[12-13]。出于完整性考虑，在此列出模型的主要特征：

(2)

(3)

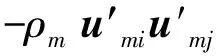
1.2 物理模型

本研究所用物理模型与文献[11]所用模型一致，具体结构尺寸如图1(a)所示，并通过ICEM软件对计算域进行六面体网格划分，划分结果如图1(b)所示。在数值模拟前需要对计算域进行网格的划分，当网格数量过少时其计算的单元较少，不能完全将组合涡流场中的参数值精确地描述出来；当网格数量较多的时候将增加计算机的计算时间，因此合适的网格数量是提高计算精度、加快计算时间的关键[10-11]。为了确保网格数量对模拟结果的影响较小，分别对网格数量为300 000、350 000、400 000、450 000这四种网格数量进行模拟计算，并在模型的Z=-72 mm的轴向位置处截取轴向速度值，确定轴向速度值变化较小的范围，并将其作为模拟网格数，可以更加接近实际分离机理，并且在一定程度上节省了计算机资源的消耗。

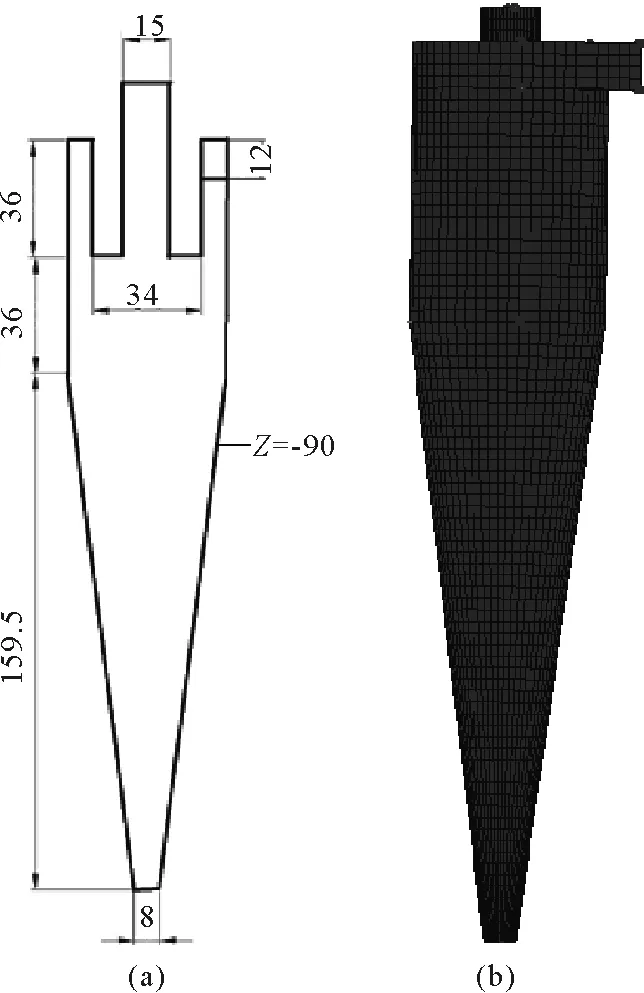
图1 水力旋流器结构与网格划分Fig.1 Structure and meshing of hydrocyclone

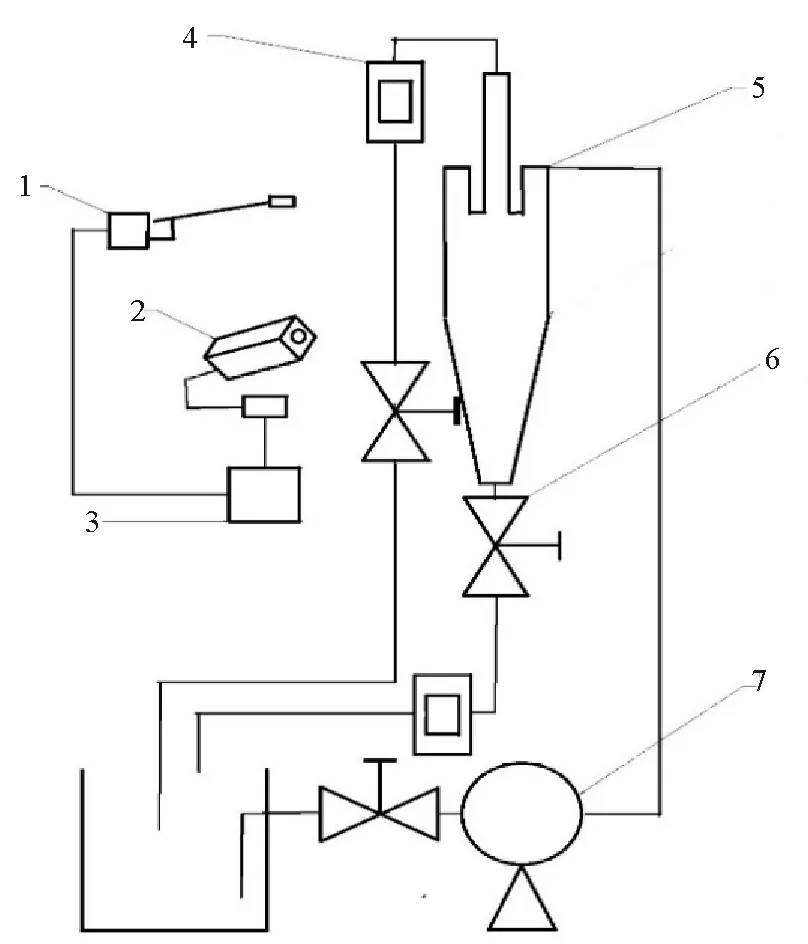
1—激光发生器；2—CCD相机；3—计算机；4—流量计；5—水力旋流器6—阀；7—蠕动泵图2 PIV装配示意图Fig.2 PIV assembly diagram

为了验证计算模型与CFD数值模拟的可靠性，选用同样结构尺寸的水力旋流器进行实验研究，并且在初始条件的设置上与数值模拟条件相同。本研究对水力旋流器内部流场进行PIV测试实验。并且在Z=-72 mm的轴向位置处截取一条直线用于轴向速度的比较分析。PIV测试实验台装配示意图见图2。

通过对图3的分析可以看出当网格数量达到40万时，随着网格数量的增加模拟的轴向速度值变化幅度很小，最大不大于0.1 m/s。并且通过PIV实验与CFD数值模拟的速度值比较可以看出，两条速度曲线基本吻合，这与文献[14]模拟所得结果相似。图中显示的PIV实验的速度曲线在中间处的中断是由于空气柱造成的。基于以上分析可以得出CFD能够很好地预测水力旋流器的内流场。

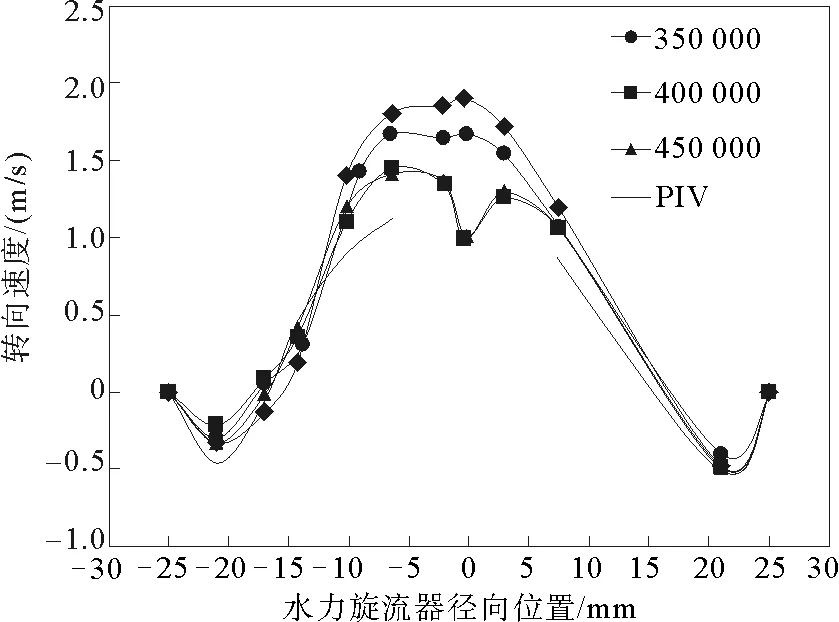
图3 水力旋流器网格无关性与模拟可靠性验证曲线图Fig.3 Mesh independence and simulationreliability verification of hydrocyclone

1.3 模拟条件

通过对压裂现场精细化过滤阶段返排液的采集与分析得出，固体颗粒悬浮物直径在50 μm以下，固体体积分数为4.37%，密度为2 650 kg/m3。研究发现，随着破胶程度的增加，压裂返排液的粘度越小，因此为了准确并且定量表述模拟及实验结果，将破胶程度用粘度表示；通过对破胶后的压裂返排液粘度多次测量得出压裂返排液的粘度在6 mPa·s以下，密度为1 020 kg/m3，在此取四组粘度(1、2、4、6 mPa·s)的压裂返排液作对照。

入口边界条件设置为速度入口，溢流和底流出口设置为压力出口，壁面设置为无滑移壁面条件[15-16]，水力旋流器的进料为压裂返排液和石英砂的混合物，处理量为29 L/min，并且两种物质的进口速度相同。模拟过程中所用的固体颗粒粒度分布与体积分数如表1所示。

表1 压裂返排液颗粒粒度分布Tab.1 Particle size distribution of fracturing flow-back fluid

图4 Z=-90 mm压力分布曲线图Fig.4 Characteristic curve of pressure (Z=-90 mm)

2 模拟结果及分析

2.1 压强及压降

水力旋流器径向压力场中的压力梯度也是使得颗粒或者流体移动的一个重要因素，并且在宏观上，水力旋流器中能量的损失表现为进出口压强降，因此对一个水力旋流器压强及压强降的研究对于内流场的分析及分离效率的提高至关重要。图4为不同粘度流体下同一轴向位置处的压力分布曲线图。

基础参数下水力旋流器的总压降

Δp总=RfΔpiu+(1-Rf)Δpio，

(4)

式中：Δp为压强降；Rf为沉砂分流比；Δpiu为底流口压降；Δpio为溢流口压强降。

通过对图4与表2的分析可以看出，在自由涡区随着粘度的增大压强在不断地降低，越靠近壁面压强降低的越明显，并且在壁面处随着粘度的增加，压强与总压强降在均匀的降低。当粘度大于2 mPa·s时粘度每升高2 mPa·s，压强平均降低7 660 Pa，压强降平均降低8 706 Pa，粘度对水力旋流器内流场自由涡区压强的分布呈线性变化，通过对图4中压强分布曲线的分析可以看出，压强在水力旋流器内流场中呈现出不完全对称分布的状态，这是由单给料入口结构造成的。在强制涡区，随着粘度的增加压强的变化并不明显，尤其当粘度在2 mPa·s以上时，空气柱中心处的压强值稳定在-8 060 Pa左右，当粘度为1 mPa·s时压强值约为-4 952 Pa。

表2 水力旋流器压降表Tab.2 Pressure drop of hydrocyclone

2.2 空气柱

通过对水力旋流器的研究[17]，认为空气柱是水力旋流器中压力能与动能转换的产物，空气柱并不参与分离却增加了能量的损失。在某些场合空气柱的存在与水力旋流器的最佳分离性能直接相关，空气柱的形态与内部流场的稳定性密切相关并且决定了水力旋流器的分离能力下限。

图5 压力与空气柱分布图Fig.5 Pressure and air cone distribution

通过图4可以看出，以水力旋流器中心轴为基准沿径向-8～8 mm的区域(空气柱及其附近区域)，压强值在急剧减少，压降值急剧的增大，增大量约占整个内流场压降值的一半，从而验证了水力旋流器中空气柱的存在确实增加了分离过程中能量的损失。并且通过对轴向位置Z=-90 mm处的压力值的研究发现，随着流体粘度的增大，内流场中的负压区域也在变大，即负压区域最小值出现在粘度为1 mPa·s处，直径约为4.71 mm，负压区域最大值出现在粘度为6 mPa·s处，直径约为5.19 mm。形成负压的区域即为空气柱存在的区域，因此随着粘度的增加空气柱的直径也在增加。

图5为压力与空气柱分布图，图中深色的区域即为空气柱，通过云图观察到空气柱会随着流体粘度的增加直径在不断变大。图中溢流管的底部形成了一个凸起，这是由于从底流口与溢流口进入的空气在此相遇产生的，这也验证了并不是由于压力梯度的存在使得液体内部溶解的气体由于向心浮力的作用而形成空气柱的观点[17]。随着流体粘度的增加溢流管底部的凸起更加明显，这是由于负压区域的增大使得吸入的空气增多，从而导致空气在此处的碰撞更加剧烈。

2.3 切向速度

切向速度是产生水力旋流器中离心惯性力的前提，在三维速度场中占据着最为重要的地位，通过对忽略重力的伯努利方程进行整理可以得出水力旋流器的组合涡流场通式：

utrn=c。

(5)

式中：ut为流体在给定点的切向速度，m/s；r为流体的旋转半径，mm；n为组合涡运动指数；c为常数。

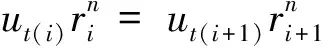
(6)

式中：ri为第i个监测点处的旋转半径，vt(i)为监测点处的切向速度，ni～(i+1)为两检测点处的组合涡运动指数。图7显示了在水力旋流器Z=-90 mm处沿径向位置的组合涡运动指数n的变化趋势。

通过对图6的研究发现，随着粘度的变大，切向速度均匀减小并且峰值越靠近空气柱附近区域。当流体粘度为6 mPa·s时切向速度峰值距离空气柱最近，出现在r=4.5 mm附近，峰值约为5.18 m/s；当流体粘度为1 mPa·s时切向速度峰值距离空气柱最远，出现在r=8.2 mm附近，峰值约为6.85 m/s。切向速度的减小将减小固体颗粒在内流场中的离心惯性力，不利于固体颗粒往壁面方向的移动，将使分离效果变差[18]。

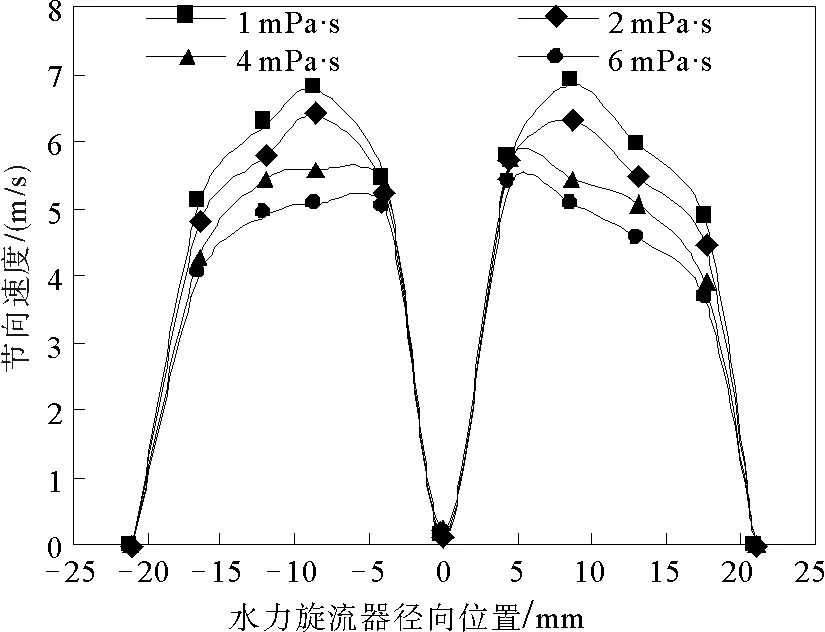
图6 切向速度特征曲线图Fig.6 Characteristic curve of tangential velocity

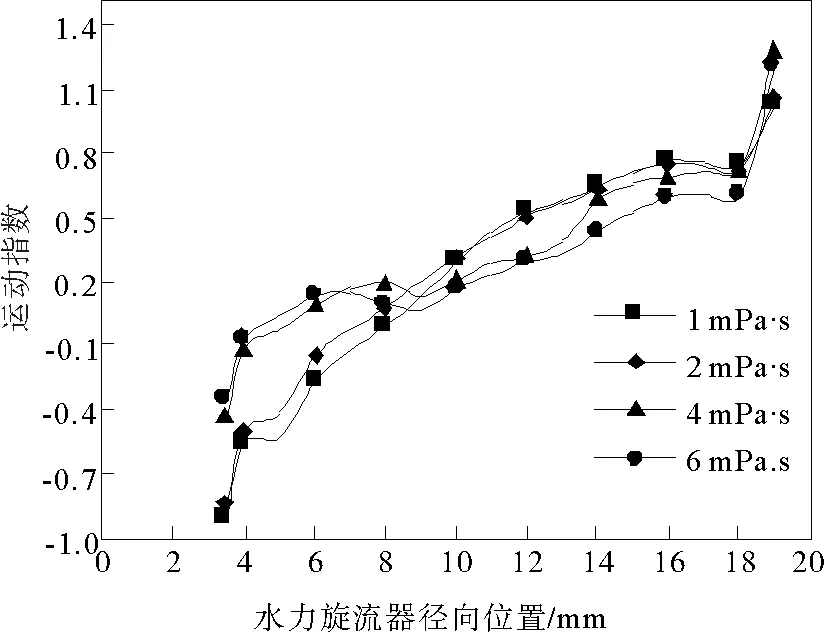
图7 组合涡流场运动指数n特征曲线图Fig.7 Characteristic curve of n

图7为组合涡运动指数n沿水力旋流器径向位置的变化趋势特征曲线图，从图中可以看出曲线的两端有突然增大的趋势，这是由于空气柱与边界层区域造成的，因此在研究过程中忽略空气柱与边界层区域。通过研究发现粘度只改变了n值的大小并不会改变n值的变化趋势，随着粘度的变大n值在减小，即切向速度的变化梯度变小，颗粒沿径向的移动速度减慢；当粘度为1 mPa·s时强制涡区的半径约为7.97 mm，当粘度为6 mPa·s时强制涡区半径约为5.12 mm，即粘度的提高减小了强制涡区的范围，这将使主分离区域变大。

2.4 轴向速度

轴向速度的大小影响着颗粒在水力旋流器中的滞留时间。在相同离心力的作用下，轴向速度较小时固体颗粒在水力旋流器内部的淘洗时间变长，有利于固体颗粒往边壁移动，促进了固体颗粒的分离。通过对图8沿轴向位置Z=-90 mm处的轴向速度分布云图可以看出，随着流体粘度的增大，轴向速度不断增大，轴向速的最大值出现在流体粘度为6 mPa·s的轴心处，速度约2.73 m/s。轴向速度的最小值出现在流体粘度为1 mPa·s的边壁处，速度约-0.78 m/s。随着分离流体粘度的增加，颗粒在水力旋流器中的停留时间变短，使得更多的固体颗粒通过溢流管排出，分离效果变差。

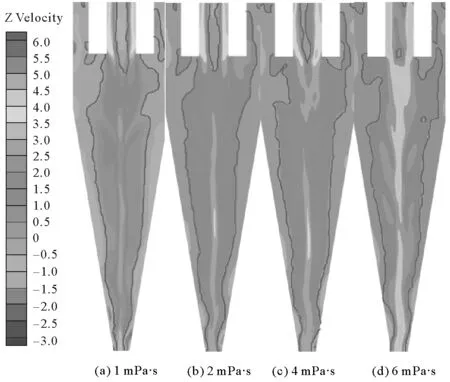
图8 LZVV与轴向速度图Fig.8 LZVV and axial velocity distribution

零速包络面(locus of zero vertical velocity，LZVV)指的是水力旋流器内流场中轴向速度为0的曲面，也是轴向速度方向发生改变的转折面，在水力旋流器中的位置如图8所示。图9为LZVV半径曲线图，从图中可以看出LZVV在锥段的中下部与溢流管区域偏摆较大，在溢流管底部至锥段中部区域波动较小。理论上，在水力旋流器中LZVV以内的流体区域全部通过溢流管排出，以外的区域全部通过底流口排出。通过对图中LZVV半径曲线分布的研究发现，随着粘度的增加切向速度的减小造成LZVV向外移动，使得自由涡区减少，从而减小了实际参与颗粒分离的区域。

3 实验研究

为了确保实验的准确性，通过水与甘油按一定的比例混合得到粘度分别为1、2、4、6 mPa·s的水溶液。取不同粒径颗粒的石英砂并按照表1所展示的比例加到不同粘度的溶液中并充分混合，用来模拟不同破胶程度下的压裂返排液。试验装配图见图10，当实验系统稳定之后，分别从溢流管与底流管取样，通过称量、抽滤和烘干测定产物的流量，采用激光粒度仪测量各产物的粒径，并进行分析。

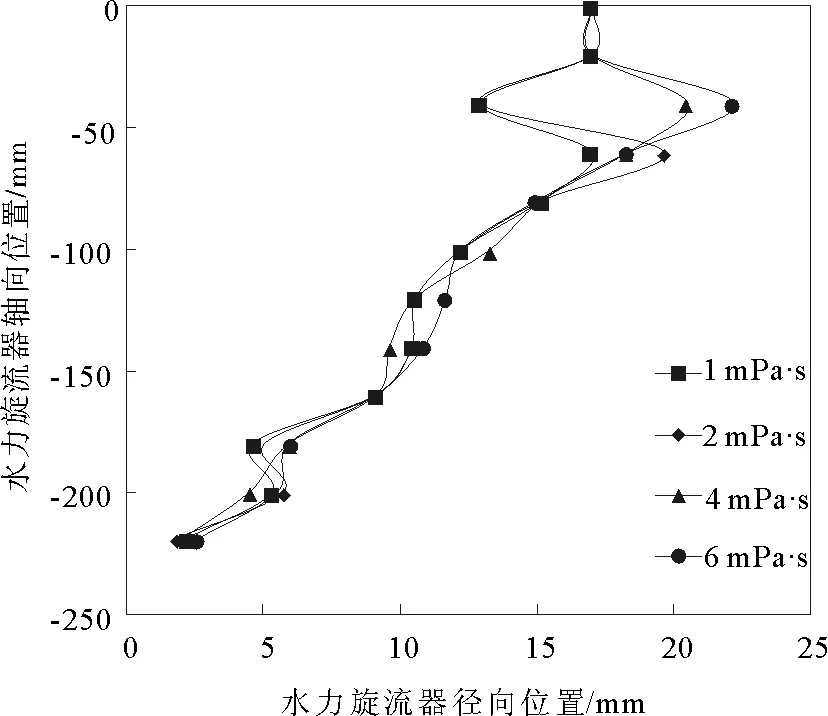
图9 LZVV半径曲线Fig.9 Characteristic curve of LZVV radius

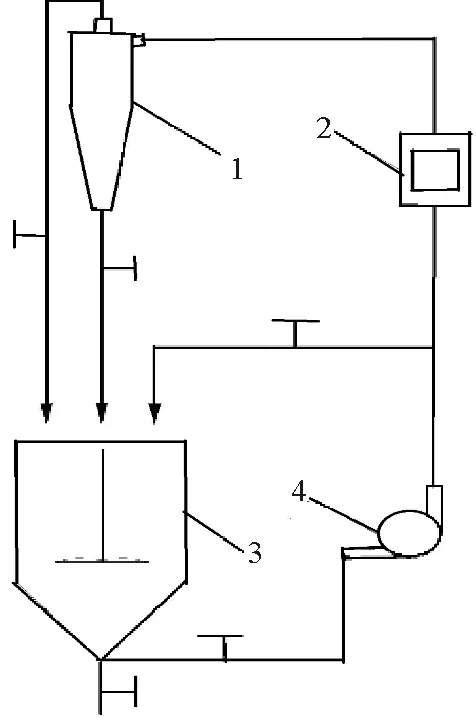
1—水力旋流器；2—流量计；3—搅拌桶；4—泵图10 水力旋流器实验装置示意图Fig.10 Experimental setup of hydrocyclone

通过对图11的分析可以看出：随着颗粒直径的增大，颗粒的分离效率呈上升的趋势，并且粒径为10 μm的颗粒分离效率随粘度的变化最小，尤其在粘度超过2 mPa·s时，分离效率的变化量仅为0.02左右。粘度为1 mPa·s与2 mPa·s的流体对粒径大于40 μm的固体颗粒分离效率差别不大，当粒径为50 μm时，粘度为1 mPa·s的流体分离效率仅比粘度为2 mPa·s的分离效率高0.009。

从图12中可以看出：当粘度从1 mPa·s增加到3 mPa·s的时候，对直径为20 μm与30 μm的颗粒的分离效率影响较大；然而随着粘度的继续增大，直径为20 μm与30 μm颗粒的分离效率趋于平缓；颗粒直径为40 μm颗粒的分离效率在粘度为2 mPa·s至4 mPa·s时变化较大；直径为10 μm颗粒分离效率受粘度的影响最小，仅在粘度从1 mPa·s增加到2 mPa·s时变化较大，当粘度大于2 mPa·s时效率变化量仅为0.05。并且从整体来看，不同粒径的颗粒在不同的粘度下的分离效率变化趋势也不相同。

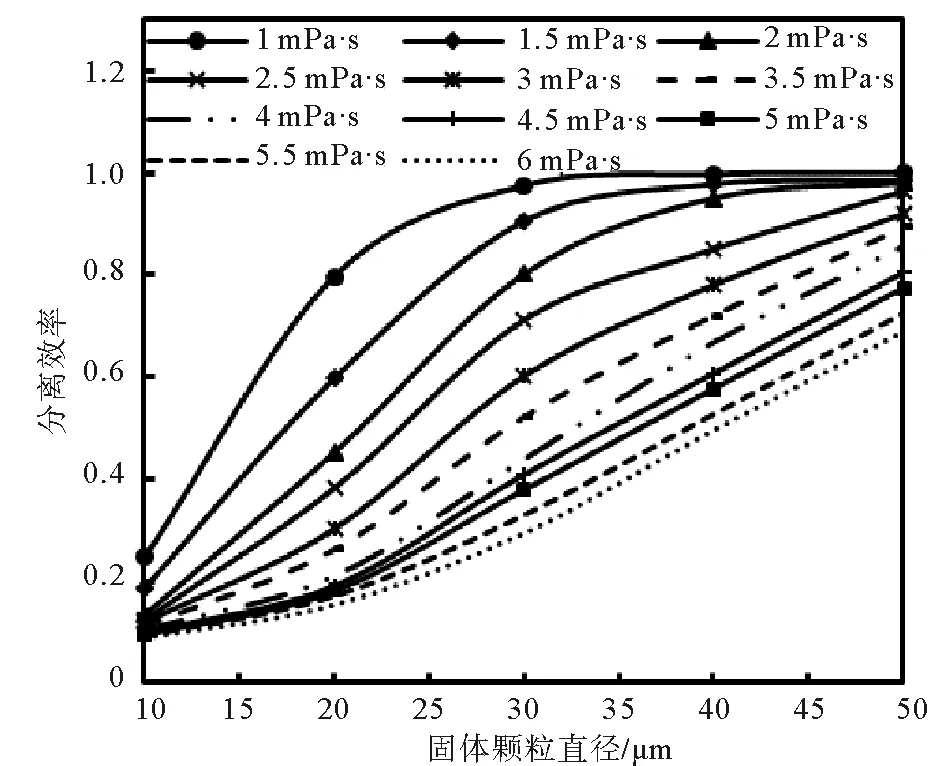
图11 不同粘度下压裂返排液分离效率曲线图Fig.11 Separation efficiency of fracturing flow-back fluid under different viscosity

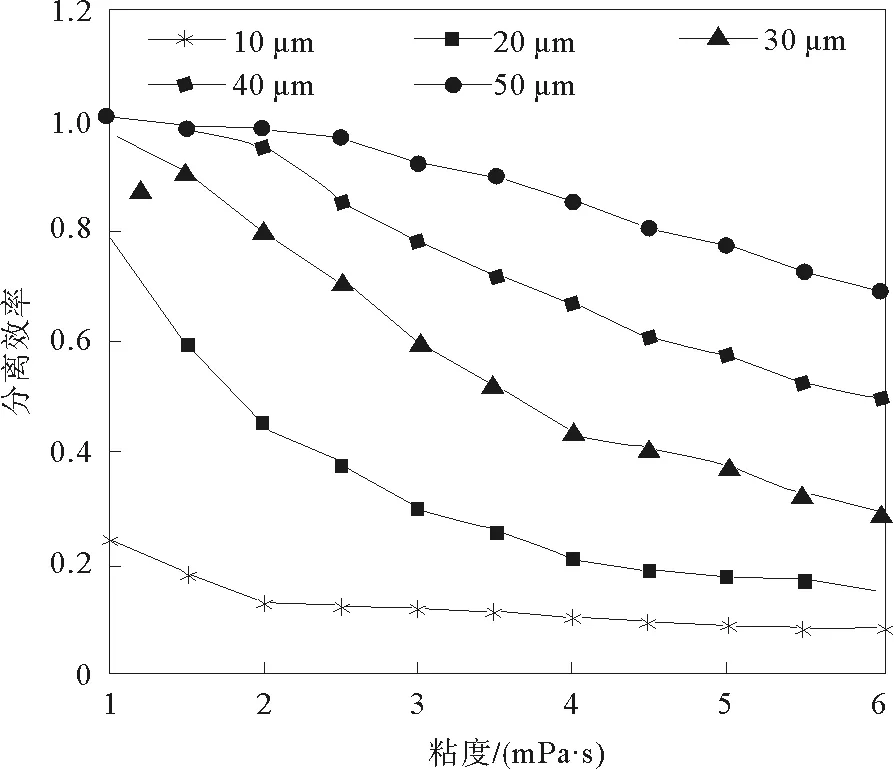
图12 粘度对不同粒径分离效率的影响Fig.12 Effect of viscosity on separationefficiency of different particle sizes

图13 粘度对分离总效率的影响Fig.13 Effect of viscosity on total separation efficiency

图13为不同粘度下颗粒分离总效率的实验值与模拟值对比，可以看出实验值与模拟值基本吻合，一方面证明了数值模拟的可靠性，另一方面可以看出随着粘度的增大，水力旋流器的分离效率急剧减小，尤其表现在粘度从1 mPa·s增大到2 mPa·s时，分离效率减小19.50%。随着粘度的增加固体颗粒分离效率的减小程度有变缓的趋势。流体粘度从1 mPa·s增加到6 mPa·s时，固体颗粒的分离效率减小了54.85%。基于以上分析可以看出粘度与分离效率的大小密切相关，因此在精细化过滤阶段应尽可能提高压裂返排液的破胶程度来降低压裂返排液的粘度。

4 结论

1) 破胶程度对压强的分布影响较大，破胶程度减小，压强显著降低并使得负压区域由粘度为1 mPa·s时的3.61 mm增加到粘度为6 mPa·s时的4.54 mm；底流口与溢流口进入的空气增多，增大了内流场的不稳定性，使得错位离子增多并减小了实际参与分离的面积。

2) 模拟结果表明，随着破胶程度的减小，切向速度持续减小，粘度为6 mPa·s的切向速度平均值比粘度为1 mPa·s的平均值减少了0.84 m/s；组合涡运动指数减小，切向速度变化梯度减小，固体颗粒物在内流场中所受离心惯性力减小。破胶程度减小使得轴向速度持续增加，零速包络面向边壁处移动，减小了固体颗粒在内流场中的停留时间以及实际参与颗粒分离的区域。

3) 实验结果表明，破胶程度对水力旋流器的分离总效率影响较大，当流体粘度从1 mPa·s增长到6 mPa·s时，固体颗粒分离效率减小了54.85%；粒径越小颗粒的分离效率所受破胶程度的影响越小，粒径为10 μm的颗粒在粘度大于2 mPa·s时，分离效率减小了2%。