基于ARIMA预测模型和混合补偿算法的医用耗材检漏仪应用研究

(山东科技大学 电子信息工程学院，山东 青岛 266590)

医用导管耗材(刚性较强的医用橡胶导管、玻璃容器等)的气密性检测是保证医用耗材安全可靠的必要检测步骤[1-2]。在以洁净空气作为检测介质的检测方法中主要有直压式、差压式、恒压式检测方法，其中差压检测法由于可靠性高、精度高、检测时间短、无污染得到了广泛应用[3]。在差压检测法中，硅压阻式传感器的温度漂移是造成精度损失的主要原因[4-7]。

目前常用的补偿方法是对传感器进行软件温度补偿，通过计算不同温度下的拟合系数来生成相应的输出函数，通过多种优化算法进行温度补偿可以获得较高的测量精度和工作可靠性。另外，基准电压的不稳定性同样对采样精度有较大影响，因此还需要进一步提高差压检测法的检测精度，减小压力传感器的精度损失，本研究通过对温度和基准电压进行混合补偿来提高检测精度。

压差检测数据序列是经典的时间序列，因此可以采用时间序列预测的方法，以一段数据序列为基础做出预测，在验证预测精度达标的情况下达到缩短检测时间的目的。目前应用较为广泛的时间序列预测方法多基于神经网络和线性统计，而基于线性统计的方法对于非线性时间序列的建模与预测能力较弱且缺乏灵活性，泛化能力不足[8-10]。基于神经网络的预测方法由于传统的网络结构确定方法和权值连接存在不足，限制了神经网络的预测能力[11]。众多研究指出单一的预测模型无法对所有的时间序列达到最优效果，针对不同的数据特征需要选择适应的预测方法[12-15]。为提高模型的预测能力，多种预测方法组合的预测模型往往能够获得优于单一预测模型的预测效果[16]。自回归移动平均(autoregressive integrated moving average，ARIMA)模型适合对时间序列的线性部分进行估计[17-20]，而单一方法的预测结果往往存在较大误差，所以需要使用神经网络对建模误差进行修正。本研究采用ARIMA与配备WASD(weights and structure determination，权值与结构确定算法)算法的幂激励前向神经网络(power-activation feed-forward neuronet,PFN)加权组合的方法，将检测序列的线性结构部分使用ARIMA模型进行估计，使用幂激励前向神经网络对非线性部分进行估计，最后将两个模型的加权组合作为最终预测模型，组合权值由测试结果确定。

1 检测原理

在检测时，气源经过灭菌过滤到达减压阀，调定好测试压力，控制器打开通气电磁阀，气体被充进检测气路，充气完毕后开始通过压力传感器检测压力变化。检测完毕后更换测试件同时放气。控制器根据检测数据计算出对应的测试参数，输出检测结果并保存测试件标号及测试数据。由于在充气过程中会伴随着发热现象，同时电磁阀关闭时也会产生压力冲击，所以存在充气造成的温度变化、压力不稳定等影响因素，多数检测方法通常需要一个平衡时间让气压达到稳定状态再进行气压及泄漏量的检测。为减少检测时间，本研究通过在平衡时间内使用加权移动平均滤波算法，把检测到的压差处理为平滑曲线，从而能够反映出气压的大致变化。利用这段时间的检测数据可以得到稳定时间内的方差变化和极差，为检测结果提供判断依据。

为分析方便，在检测过程中可以将气体看作理想气体状态，其公式为：

(1)

(2)

检测过程中的温度变化通常被忽略，认为是等温状态，在大气压下的泄漏量、泄漏极差和方差可以分别表示为：

(3)

R=P-P1，

(4)

(5)

2 ARIMA-WASDN预测模型

2.1 ARIMA预测模型

气密性检测过程得到的压差数据是一个典型的时间序列，具有较强的趋势特征，为达到缩短检测时间的目的，可以采用时间序列预测的方式来减少检测时长。检测过程中，先将时间序列分解为线性自相关部分和非线性部分，使用ARIMA模型对线性自相关部分进行建模，然后使用WASDN对ARIMA的建模误差进行建模，得到ARIMA的建模误差。

ARIMA模型能够有效地对线性的时间序列进行建模与估计，是由Box等[12]提出的用来处理时间序列预测问题的经典方法，通过时间序列的历史数据对序列的未来值做出预测。预测过程主要包括平稳性检测、数据预处理以及平稳化处理、模型结构确定、参数估计和模型检验等步骤。预测模型的建模流程如图1所示。ARIMA模型可以表示为：

(6)

图1 预测模型建模流程图Fig.1 Forecast model modeling flow chart

对非平稳时间序列Yt进行d阶差分得到dYt=Xt，为差分算子，其中L是滞后算子(Lag operator)，d∈Z，d>0。εt,εt-1,…,εt-q为白噪声序列，可用来判断模型性能。P为自回归阶数，代表预测模型中采用的时序数据本身的滞后数(lags)；d为差分阶数，代表时间序列需要进行差分的阶数以达到稳定状态；q为移动平均阶数，代表预测模型中采用的预测误差的滞后数。

预测过程具体如下：

对原始时间序列进行数据预处理，当原始数据太多时可以进行重采样和幅值变换简化处理过程。在对时间序列进行建模前，需要检测序列的平稳性，对非平稳序列的非平稳成分(趋势、季节性及其他非平稳成分)进行平稳化处理。本研究使用迪基-福勒检验(Dickey-Fuller test，DFT)方法进行平稳性判定，零假设为序列非平稳，当检验值小于临界值时则拒绝零假设，认为数据是稳定的。回归模型可以表示为：

Δyt=(ρ-1)yt-1+ut=δyt-1+ut。

(7)

δ是回归系数，ut是误差项。DFT通过检测回归模型是否存在单位根实现，δ=0时，认为时间序列不存在单位根，序列是平稳的。通常认为越靠近一个时刻的值对于下一个时刻的值影响越大，所以可使用指数加权移动平均方法(exponentially weighted moving-average，EWMA)来对数据进行平滑处理，数值的加权系数随着时间呈指数下降，获得平滑后的序列。EWMA的表达式为：

yt=βyt-1+(1-β)θt。

(8)

其中，系数β表示加权下降的速率，yt为t时刻EWMA值；将原始序列取对数后减去平滑得到的序列，可以得到与时间无关的序列，再次做DFT验证平稳性；对原始数据做分解，可以得到数据的趋势部分、季节性部分和残留部分，通常趋势部分具有较强的趋势性，季节性部分具有明显的周期性，而剩余部分可以认为是去除了趋势和季节性数据之后的稳定的数；对于得到的稳定时序数据，通过分析自相关图(auto correlation function，ACF)、偏自相关图(partial auto correlation function，PACF)选取p，q阶数；对不同的p，d，q参数组合，通过AIC准则(akaike information criterion,AIC)得到最优的参数模型，使得赤池信息量准则达到最小的p和q即为最佳模型。赤池信息量准则定义如下：

A=-2lnL+2n。

(9)

其中：L为模型的极大似然参数，n为模型的独立参数；对模型的参数进行最小二乘估计，通过检验残差序列et是否为白噪声序列判定所建立模型的合理性，若不通过检验则重新确定模型的结构参数；得到ARIMA预测模型后，对时间序列进行预测，w步前向预测公式可以表示为：

(10)

2.2 WASDN修正模型

WASDN是具有WASD算法的幂激励前向神经网络，具有结构简单、泛化能力强和学习速度快的优点，适合多变量函数逼近和模式识别工作。为进一步提高ARIMA模型的预测精度，使用WASDN(WASD PEN，WASDN)神经网络对ARIMA建模误差进行修正，能够避免非线性部分对ARIMA模型造成的延时和精度损失。多输入PFN神经网络模型结构如图2所示。

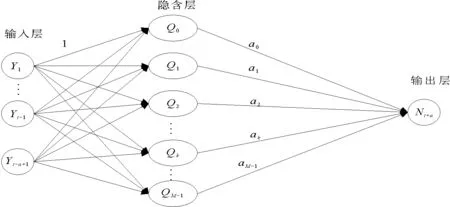
图2 PFN神经网络模型结构图Fig.2 PFN neural network model structure

该模型中，时间序列第a步的非线性部分的预测值与输入函数的关系可以表示为：

(11)

其中，Qb为激励函数，表示所有输入幂的乘积。由于输入层和隐含层神经元的数目对模型的建模和预测性能有重大影响，因此需要对模型的结构参数进行优化。通常过少的输入神经元数目无法有效建模，预测性能损失较大；而输入层过多将会引入冗余信息，降低学习速率和预测性能；并且隐含层过少将会使网络无法达到预期的逼近精度，相反则会导致过拟合。因此使用WASD来确定神经网络的权值和结构，即权值直接确定法和网络结构自确定法。具体方法如下：①根据对ACF和PACF的分析，确定网络的输入层神经元数目，可以直接选取自回归阶数p作为输入层神经元数目；②增加隐含层神经元数目，根据权值直接确定法(WDD)确定当前结构的最优连接值；③循环前向搜索建模误差更小的隐含层神经元来确定网络的隐含层神经元数目。

得到WASDN模型后，需要与ARIMA模型进行加权组合，组合方法如下：

(12)

3 混合补偿算法

3.1 温度补偿

在充气完毕后，虽然会受气压不稳定、温度变化等因素的影响，但压差变化的基本趋势是一定的。经过不间断检测得到的压差值是一组离散时间序列，若第n次采样得到压差值用X(n)表示，则第n次采样值就可以表示为：

(13)

(14)

基于最小二乘法的温度补偿算法，在不考虑温度时，传感器的输出关系为：

(15)

其中：x是传感器的数字量输出，y为压力的真实值。n次多项式至少需要n+1个数据点才能计算得出方程的解，根据经验值一般采用4次或以下的多项式拟合，本设计采用3次最小二乘拟合。将(8)式用向量形式表示：

y=(a0,a1…an)(1,x…xn)T=AX。

(16)

其中，ai是温度t的函数。

(17)

将ai代入式(8)，求解bji即可得到方程组的解，将bji表示为列向量：b=(b00,b01,…bMN)T，定义一个辅助矩阵F,Xp表示第p个测量值。

(18)

则传感器经过温度修正后的测量值为：

y=(y1y2…yp)T=Fb。

(19)

压力传感器测量的真实值为：

z=(z1z2…zp)T。

(20)

方程组的解即为z=Fb最小二乘意义下的最优解。转化为普通的线性代数方程：FTz=FTFb可由MATLAB求解得到辅助方程F的解。

3.2 基准电压补偿

在实际检测过程中发现，电源的稳定性对于检测结果的准确度具有较大的影响，因此设计了基准电压检测电路，对ADC的基准电压波动进行动态补偿。系统电源主要有24 V/5 V数字/模拟电源，PCB设计中使用电源分隔技术分别供电。为提高模拟信号的采集精度，将数字部分和模拟部分分开，通过滤波电路相连接。使用5 V模拟电压提供参考电压，用MCU片内ADC来进行基准电压补偿，对采集到的数据进行归一化处理，能够抵消电源电压纹波对于采集精度的影响。补偿方法可以表示为：

Da=ViRM1/(Vm/Im)。

(21)

其中：Da为补偿后的采集数据，Vi为外部信号的电压值，RM1为模数转换采集芯片的最大分辨率，Vm为测得的参考基准电压，Im为基准电压的准确度(Vm/RM2)，RM2为片内模数转换芯片的最大分辨率。

4 实验结果分析

实验环境为cortex-A53硬件平台，采用Python语言编程，使用24位高精度模数转换芯片CS5534采集传感器压差信号，以400 mL耐压瓶作为实验对象。在环境温度为289.75 K、充气压力为240 kPa的一次检测过程的温度变化如图3所示。对原始数据做分解，得到数据的趋势部分、季节性部分和残留部分如图4所示。可以看到趋势部分具有较强的趋势性，季节性部分周期性较弱，因为达到稳定环境后周期性干扰较少，而图4(d)是剩余的部分，可认为是去除了趋势和季节性数据之后的稳定数据。对于得到的稳定时序数据，通过自相关和偏自相关进行ARIMA参数估计，由前文中的差分结果可知，一阶差分后数据已经稳定，所以d为1。如图5所示，自相关和偏自相关图都存在拖尾的特点且具有明显的一阶相关性，确定p为1，q为1。得到参数估计值后，生成模型ARIMA(p,d,q)，p=1,d=1,q=1。模型拟合效果对比如图6所示(点线图为拟合后的曲线，线图为原曲线)，图6(a)为ARIMA模型的拟合效果，图6(b)为AR模型的拟合效果，由RSS可知相比AR模型ARIMA模型能够获得更小的拟合误差，所以ARIMA模型(ARIMA(1,1,1))的拟合效果更好。使用已经测得的数据进行模型预测，采用循环测试对比对称均值绝对值百分比误差(symmetric mean absolute percentage error,SMAPE)得到测试误差，当测试误差最小时得到的α为ARIMA与WASDN的组合权值。

在有泄漏的环境下对不同温度和不同充气压力进行多次重复性测试的部分数据如表1所示。

由图3的温度变化曲线可知，检测过程中由于充气导致的气体压缩温度快速上升，在充气完毕后温度值逐渐回落至比初始温度高约0.15 K的水平，温度变化曲线充分反应了充气过程对于检测环境造成的温度变化。根据《专用检测设备评定方法指南》(JB/T 10633-2006)，准确度和重复性是评定检测设备性能的两个主要指标，当Cg≥2及Ckg≥2时符合用于评定设备的日常周期检测的合格评定标准。从表1可以看出，在充气压力为270 kPa/有泄漏时的不同温度下，示值误差较小，准确度和重复性指标Cg和Ckg均>10，满足评定标准。在温度为220 ℃/有泄漏的不同压力下，示值误差均<0.2，准确度和重复性指标Cg≥2、Ckg≥2，预测SMAPE均小于15%，预测性能良好，满足评定标准。

图3 温度变化曲线图Fig.3 Temperature curve

图4 数据成分分解图Fig.4 Data component decomposition diagram

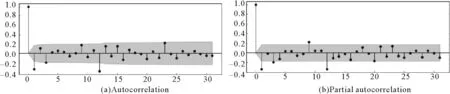
图5 自相关、偏自相关图Fig.5 Autocorrelation,partial autocorrelation diagram

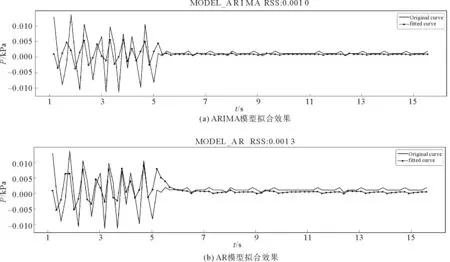
图6 模型拟合效果对比图Fig.6 Comparison of model fitting effects

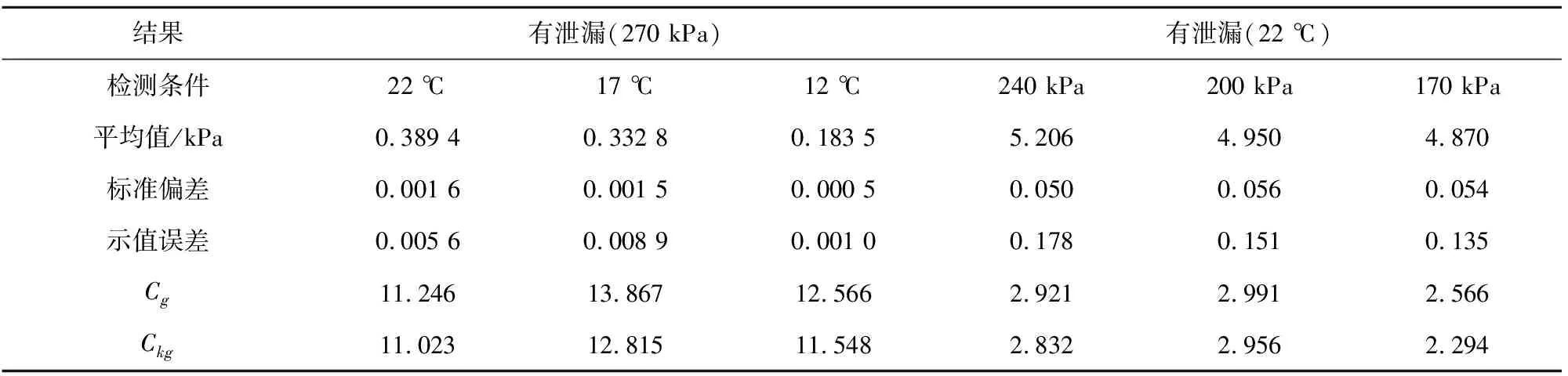
结果有泄漏(270 kPa)有泄漏(22 ℃)检测条件22 ℃17 ℃12 ℃240 kPa200 kPa170 kPa平均值/kPa0.389 40.332 80.183 55.2064.9504.870标准偏差0.001 60.001 50.000 50.0500.0560.054示值误差0.005 60.008 90.001 00.1780.1510.135Cg11.24613.86712.5662.9212.9912.566Ckg11.02312.81511.5482.8322.9562.294

5 结语

为了提高医疗耗材检漏仪的实用性，本研究应用混合补偿算法对压差传感器和基准电压进行补偿，减弱了电源电压波动对于基准电压的影响，提高了检测精度；搭建了基于ARIMA的压差预测模型，采用幂激励前向神经网络对建模误差进行修正。运用测得的监测数据进行预测对比，对称平均百分比误差小于15%，预测性能良好。实验结果表明，本方案能够在40 s以内判断泄漏结果，重复性和准确度均符合评定标准，提高了设备的易用性。