不连续时滞分数阶忆阻神经网络的非线性动力学分析
2019-05-22
(山东科技大学 电气与自动化工程学院, 山东 青岛 266590)
1971年,华裔科学家蔡少棠[1]根据概念的对称性首次提出了忆阻器的概念,描述了磁通和电荷之间的非线性关系。2008年,惠普公司研究团队首次实现了具有TiO2双层薄膜结构的实物忆阻器[2]。由于忆阻器的阻值依赖于电压或电流的作用时间而非当前时刻的瞬时值,从而使得忆阻器成为天然的非易失性存储器,即当忆阻器两端电压(或电流)掉电时,忆阻器仍然能记忆其当前时刻的电阻值。文献[3]研究表明忆阻器能够模拟大脑中的神经突触,由于忆阻器的这种记忆特性,越来越多的研究者用忆阻器代替传统神经网络中的电阻来构建忆阻神经网络[4]。近年来,忆阻神经网络(memristive neural networks,MNNS)的动力学行为得到了广泛的研究[5]。
分数阶微积分目前在各个领域都得到了广泛的应用。相较于整数阶微积分,分数阶微积分最主要的优点在于其具有记忆特性,这使得它为描述具有遗传和记忆特性的各种物质和过程提供了更新颖的、准确的数学工具[6]。文献[7]表明分数阶微积分能够更精确地刻画小鼠大脑新皮层锥体神经元的动力学行为。鉴于此,为了更好地描述大脑神经元的动力学过程,一些研究人员将分数阶微积分引入到神经网络中,建立了分数阶神经网络模型[8]。神经网络可以由超大规模集成电路(vary large scale integration,VLSI)来实现[9]。在整数阶神经网络中,电容是整数阶的。然而,大量研究表明电容实际上是分数阶的[10]。为此,研究人员用分数阶电容代替整数阶电容来构建神经网络电路,以提高模型的精确度,从而建立了分数阶神经网络。与整数阶神经网络相比,分数阶神经网络的非线性更强,且具有更多自由参数。近年来,关于分数阶神经网络的动力学研究取得了巨大的进展[11]。
为了更精确地描述大脑神经元的动力学行为,研究人员结合忆阻器和分数阶微积分的优点建立了分数阶忆阻神经网络模型(fractional memristive neural networks,FMNNS)[12]。从电路实现的角度来看,FMNNs可以通过将整数阶忆阻神经网络中的整数阶电容用分数阶电容代替来实现。虽然目前关于整数阶忆阻神经网络的动力学研究成果丰硕,但是传统的分析方法如Lyapunov方法和矩阵测度方法等都不能直接应用到分数阶忆阻神经网络中去。因此,如何将分数阶微积分理论的最新研究成果应用到分数阶忆阻神经网络的分析中来是目前急需解决的问题。分数阶和忆阻器的引入给神经网络的动力学分析带来了巨大的困难和挑战。近年来,关于分数阶忆阻神经网络的研究已经取得了一些成果[12-17]。文献[12]利用分数阶李雅普诺夫函数方法研究了FMNNs的Mittag-Leffler的稳定性。文献[14]利用不等式技术研究了时滞FMNNs的自适应同步问题。文献[15]研究了时滞FMNNs的混合投影同步。文献[16]利用比较原理研究了参数不确定多时滞FMNNs的同步问题。文献[17]利用新的Mittag-Leffler估计引理研究了参数不匹配FMNNs的准同步问题。
根据上述讨论可知,文献[5,11]研究的都是连续型神经网络的动力学,文献[13]研究了具有不连续忆导函数的FMNN的动力学行为,文献[12,14-17]主要研究了不连续忆阻神经网络的稳定性和同步问题。目前尚没有文献对不连续时滞FMNN的非线性动力学进行研究。为此,提出了一个不连续时滞分数阶忆阻神经网络模型,并研究了不同的分岔参数对系统动力学行为的影响。值得注意的是,不连续时滞分数阶忆阻神经网络的连接权重不同,使得其包含多个子系统。系统随开关阶跃T的变化而切换,使系统的动力学行为更加复杂。另外,文献[5,11]中提出的系统通往混沌的道路大多为倍周期分岔或反向倍周期分岔,而本研究提出的FMNN模型通往混沌的道路为阵发混沌,动力学行为更加丰富。不连续忆导函数和开关阶跃的加入能够极大地丰富系统的动力学行为,所得结果为不连续FMNN的应用打下基础。
1 预备知识
1.1 Caputo 型分数阶导数
定义 1[18] 函数f(t)的α阶Caputo型分数阶导数定义如下:
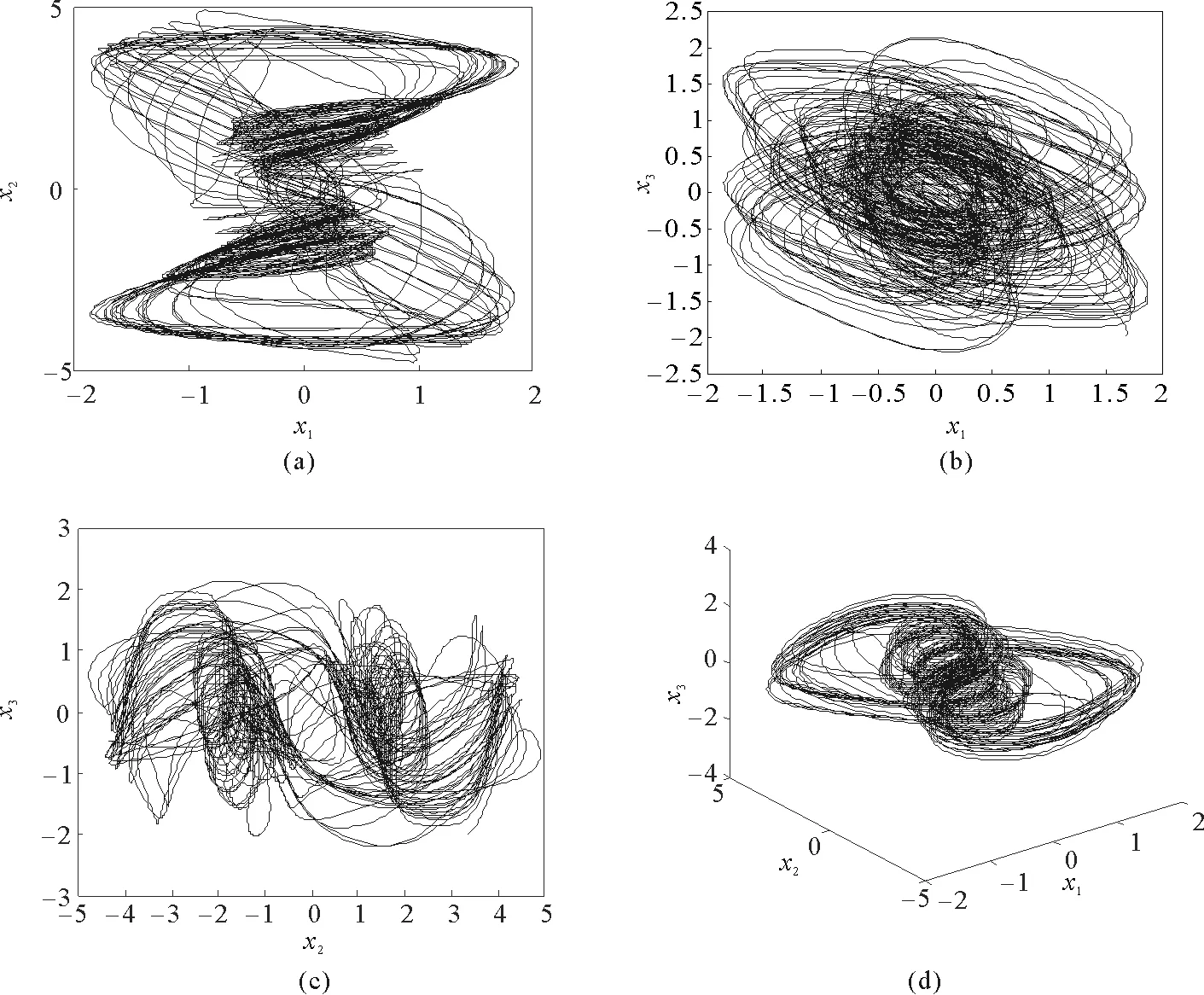
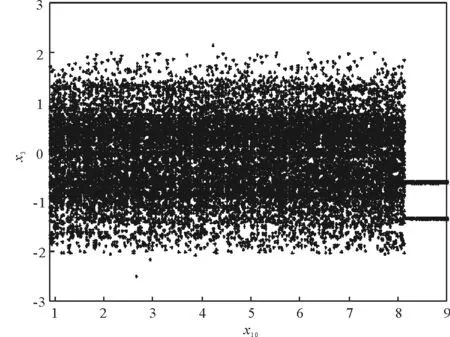
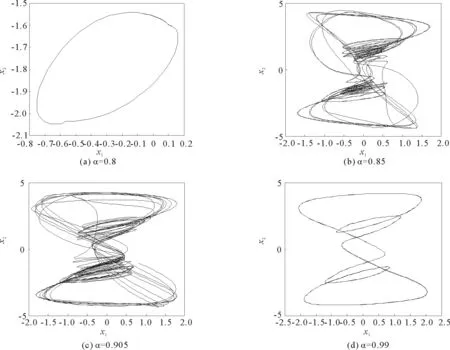
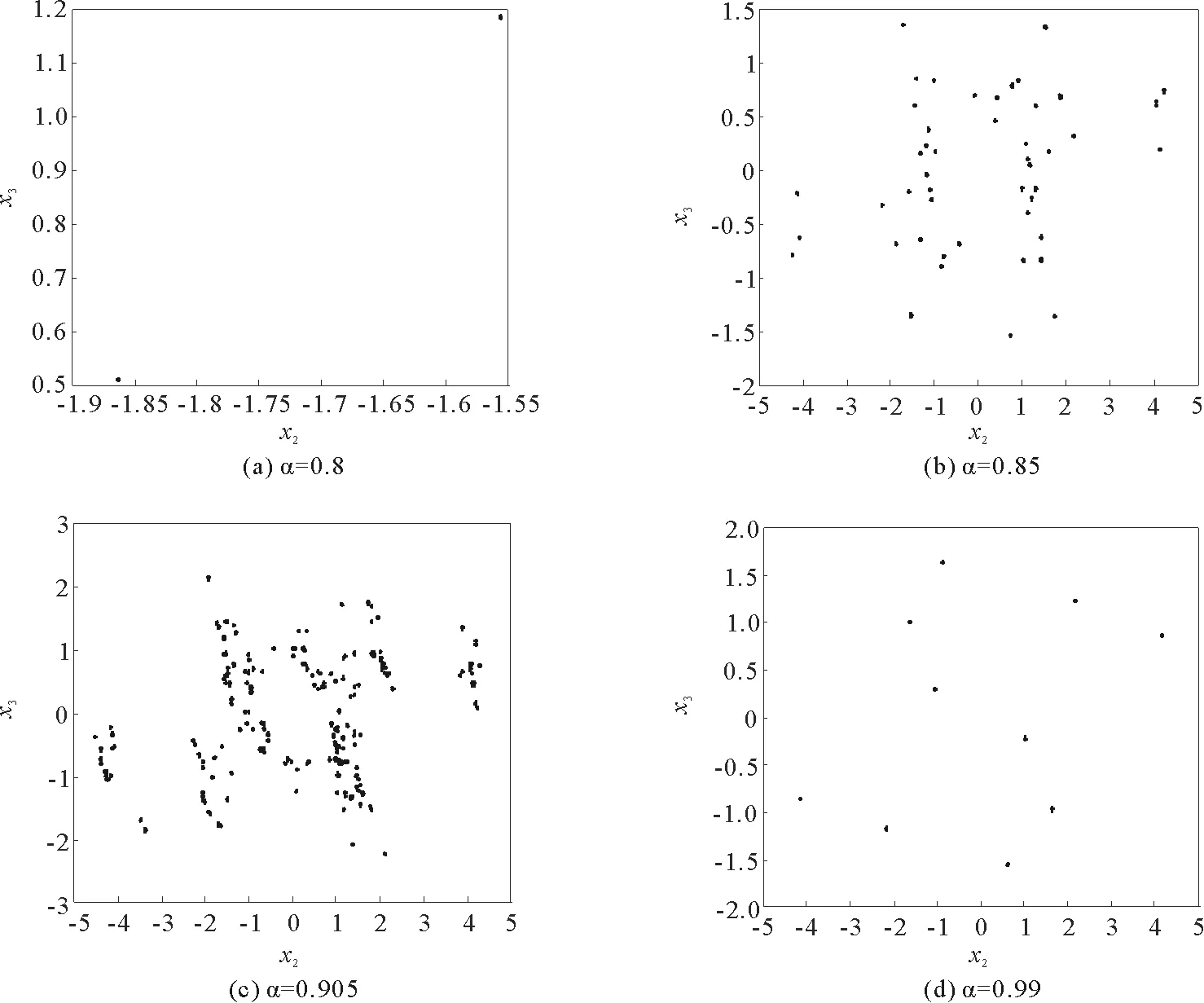
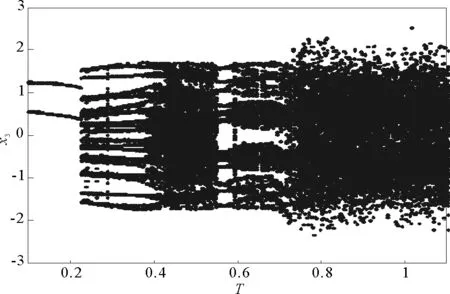
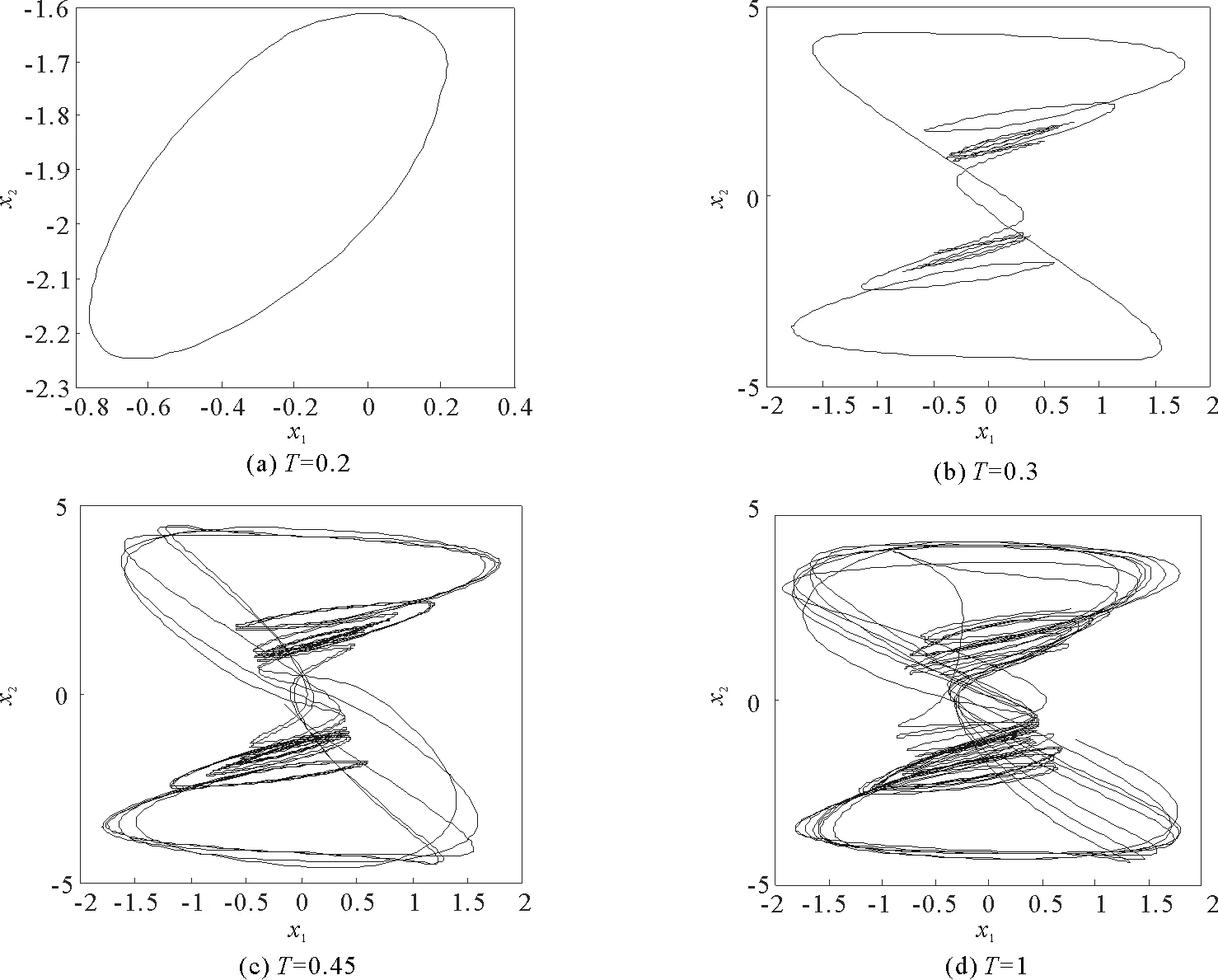
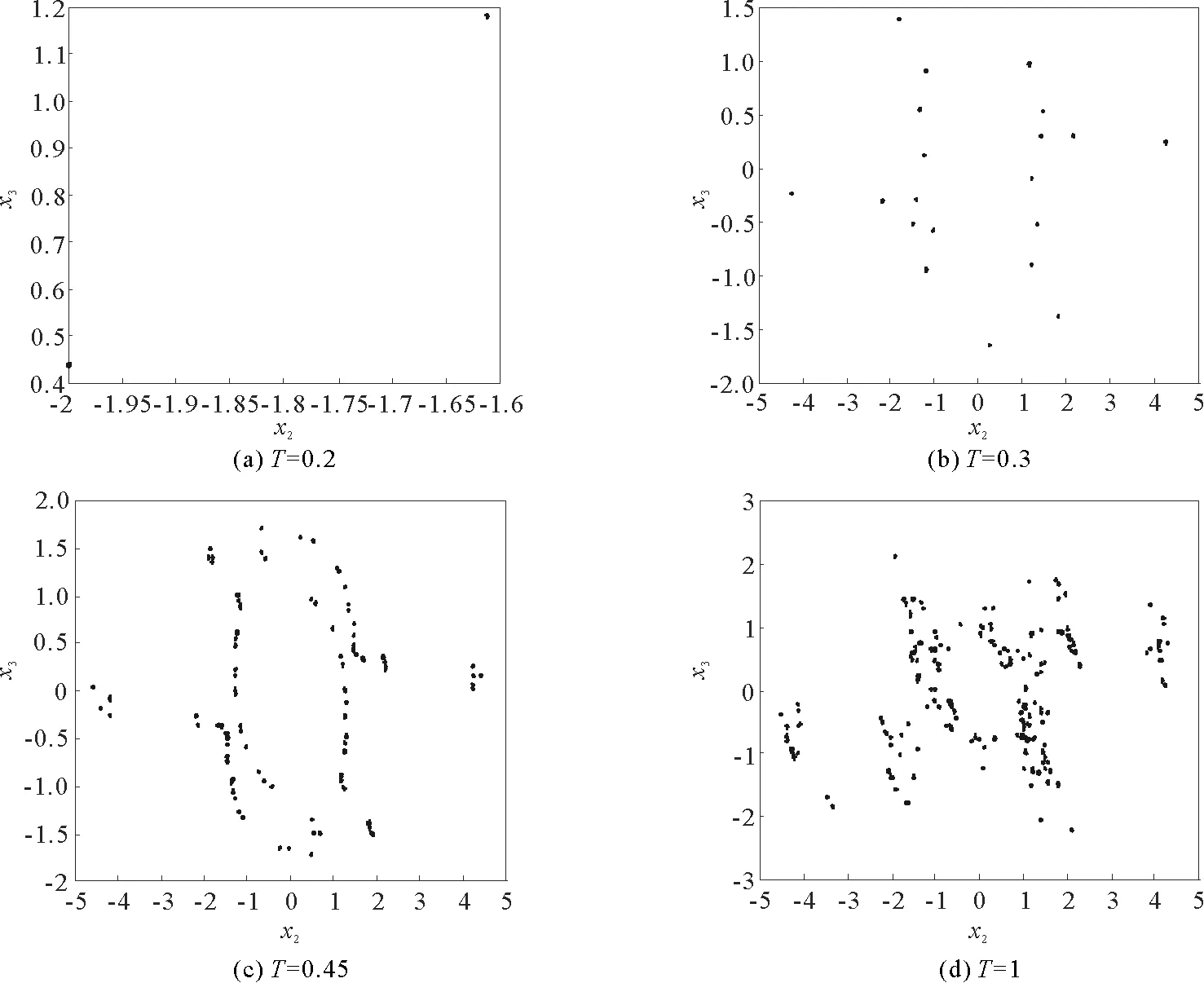
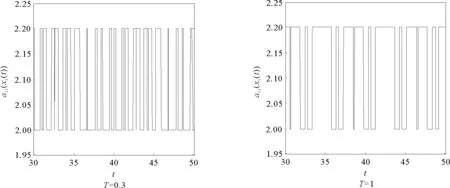
其中t≥t0,n是正整数并且满足n-1<α 忆阻器最初被用来描述磁通φ和电荷q之间的关系。磁通φ和电荷q之间的关系可以用q-φ或φ-q平面上一条过原点的特性曲线f(φ,q)=0来表征。磁通和电荷之间的关系φ=φ(q)可以定义一个电荷控制(或电流控制)的忆阻器。此时,非线性关系f(φ,q)=0能由关于电荷q的单值方程φ=φ(q)表示出来。因此,忆阻器可以用其忆阻值M(q)来表征,其电流-电压关系特性为 同样地,电荷-磁通特征关系q=q(φ)能定义一个磁通控制(或电压控制)的忆阻器。此时,f(φ,q)=0能由一个关于磁通φ的单值方程q=q(φ)来表示。由此可以推出: 考虑一类不连续时滞分数阶忆阻神经网络[14-17],表示如下: (1) 其中,i=1,2,…,n,n代表神经元的数量;0<α< 1代表分数阶;ci> 0代表自反馈系数;xi(t)为第i个神经元的状态变量;fj(·),gj(·)代表激活函数;τ代表时滞。忆阻连接系数aij(xj(t))和bij(xj(t))可以表示为: 本文提出了一个三维的不连续时滞分数阶忆阻神经网络模型,描述为 (2) 其中,将参数设置如下:c1= 2.2,c2= 1.2,c3= 1.8,τ=0.8,T= 1,fj(xj)=gj(xj)=tanh(xj),j= 1,2,3。不连续的连接权重为: 令α= 0.905,初始状态设定为x(s)= (0.9,-0.5,0.7)T,∀s∈ [-0.8,0]。如图1所示,系统(2)能够产生混沌吸引子。 图1 当初始状态x(s) = (0.9,-0.5,0.7)T时系统(2)的相图Fig.1 Phase portraits of system (2) with initial condition x(s)= (0.9,-0.5,0.7)T 图2 随x10变化的分岔图Fig.2 Bifurcation diagram with varied x10 上述分析已经验证:当α=0.905,x(s)= (0.9,-0.5,0.7)T,T= 1时,系统处于混沌状态。因此,取系统的初始状态α= 0.905,T= 1,(x1,x2,x3)T= (x10,-0.5,0.7)T,x10的变化范围为0.9~9,步长为0.02。分数阶微分方程(2)通过Adams-Bashforth-Moulton 预估-校正算法[20]求解,步长为0.005。如图2所示,当x10从0.9变化到8.12时,随着x10的增加,系统(2)表现出混沌行为。当x10从8.14变化到9,系统(2)出现周期-1轨道。 分别选取不同的x10,系统(2)的相图及相应的庞加莱截面(选取的截面为x1=0.5)如图3~4所示,仿真时间范围设为[200 s,400 s]。不同的x10对应的动力学行为如表1所示。 图3 x10取不同值时系统(2)的相图Fig.3 Phase portraits exhibited in system (2) with different values of x10 图4 x10取不同值时系统(2)的庞加莱截面Fig.4 Poincaré sections of system (2) with different values of x10 表1 x10取不同值时系统(2)的动力学Tab.1 Dynamics of system (2) for different x10 图5 随α变化的分岔图Fig.5 Bifurcation diagram with varied α 令初始状态(x1,x2,x3)T=(1,-0.5, 0.7)T,T= 1。α从0.8变化到1,步长为0.000 4。如图5所示,当α∈ [0.841 6,0.909 2],[0.910 8,0.951 6]和[0.954 0,0.951 2]时,系统(2)展现出混沌状态。当α∈ [0.800 0, 0.841 2],[0.909 6,0.910 4],[0.952 0,0.953 6],[0.961 6,0.986 0],[0.986 4,0.993 6]和[0.994 0,1.000 0]时,系统(2)表现出周期状态。 选取不同的分数阶α,系统(2)的相图及相应的庞加莱截面(选取的截面为x1=0)如图6~7所示,仿真时间范围设为[200 s,400 s]。不同的分数阶α对应的动力学行为如表2所示。 图6 α取不同值时系统(2)的相图Fig.6 Phase portraits exhibited in system (2) with different values of α 图7 α取不同值时系统(2)的庞加莱截面Fig.7 Poincaré sections of system (2) with different values of α 由图2、图5可以看出,随着分岔参数的变化,周期窗口与混沌窗口以阵发的形式交替出现,而未出现通过倍周期分岔到混沌的这种分岔过程。因此,不同于文献[5,11]中所研究的连续型系统的倍周期分岔,不连续系统(2)通往混沌的道路为阵发混沌。因此,本研究丰富了之前的结果。 令初始状态(x1,x2,x3)T= (1,-0.5,0.7)T,α= 0.905。T的变化范围为0.1~1.1,步长为0.002。当T∈ [0.392,0.544],[0.590,1.100]时,系统(2)展现出混沌状态。当T∈[0.100,0.222],[0.224,0.390],[0.546,0.588]时,系统(2)表现出周期状态。 选取不同的开关阶跃T,系统(2)的相图及相应的庞加莱截面(选取的截面为x1=0)如图9~10所示,仿真时间范围设为[200 s,400 s]。不同的开关阶跃T对应的动力学行为如表3所示。 表2 α取不同值时系统 (2) 的动力学Tab.2 Dynamics of system (2) for different α 图8 随T变化的分岔图Fig.8 Bifurcation diagram with varied T 图9 T取不同值时系统(2)的相图Fig.9 Phase portraits exhibited in system (2) with different values of T 图10 T取不同值时系统(2)的庞加莱截面Fig.10 Poincaré sections of system (2) with different values of T T动力学图0.20周期-1图9(a)0.30周期-10图9(b)0.45混沌图9(c)1.00混沌图9(d) 图11 T取不同值时a11(x1(t))的切换律Fig.11 Switching laws of a11(x1(t)) with different values of T 由于不连续忆导函数的存在,使得系统(1)本质上是一个由2n个子系统构成的切换系统。显然,新构建的系统(2)由8个子系统构成。因此,不连续忆导函数的加入可以丰富切换系统的子系统数目。特别地,本文分析了开关阶跃T对系统(2)动力学行为的影响。本文忆阻器的阻值是二值切换的,当开关阶跃T达到阈值电压时,忆阻器的阻值为一个特定的值,当开关阶跃T的值小于阈值电压时,忆阻器的阻值为另一个特定的值。忆阻器的阻值在两个值之间切换,系统展现出复杂的动力学行为。值得注意的是,不同的开关阶跃T并没有改变系统(2)的8个子系统的动力学行为,但可以改变忆阻连接权重的切换律。如图11所示,不同的开关阶跃T能够产生不同的切换律,进而可以影响或改变系统(2)的动力学行为。 提出了一个不连续的时滞分数阶忆阻神经网络模型,通过选取不同的分岔参数,对该模型进行了详细的分岔分析。利用分岔图、相图和庞加莱截面等数值仿真手段验证了其典型的动力学行为。不同于倍周期分岔,所提出的不连续分数阶忆阻神经网络通往混沌的道路为阵发混沌。同时,还揭示了不连续的忆导函数和开关阶跃T对系统动力学的内在影响机制。研究结果可为混沌生成提供新的思路和方法。1.2 忆阻器模型
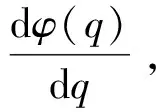

2 不连续时滞分数阶忆阻神经网络中的混沌现象
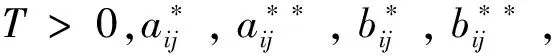


2.1 随初值x10的分岔分析
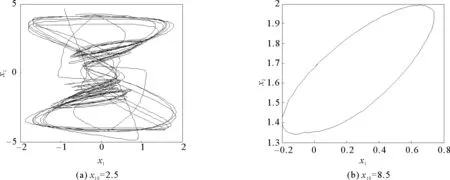


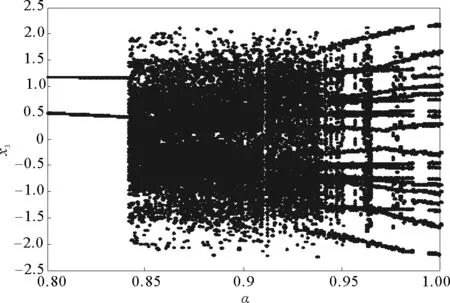
2.2 随分数阶α的分岔分析
2.3 开关阶跃T的分岔分析


3 结论
