几何解题教学用力点：图形变换后的不变性——从一道八年级全等把关题的讲评说起

☉江苏省镇江中学附属初中 张祖翼

熟悉初中各年级教学的同行都有这样的印象，学生进入初中阶段的第二次分水岭是几何的学习与证明，特别是图形变换之后数量关系之间的变化与不变性质是研究的热点问题.而对这类问题的讲评，深入思考下去，会启示我们在不同年级几何教学用力点的话题.本文从一道八年级把关题的讲评说起，对不同年级几何解题教学用力点给出笔者的理解和思考.

一、从一道八年级全等把关题的讲评说起

考题1：已知，如图1，边长为5的等边三角形ABC中，点D在边AB上，点F在边BC上，以DF为一边作等边三角形DEF，连接BE.

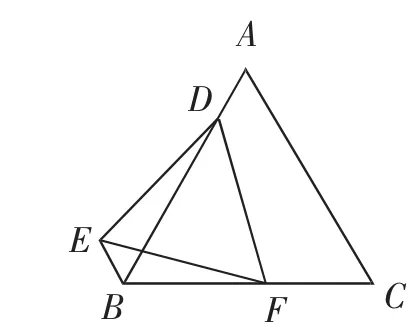
图1

图2

（1）当点D与点A重合时（如图2），求证：BE+BF=AC.

（2）如图1，当AD=1时，求BE+BF的值.

阅卷手记：这道试题位于八年级期末试卷倒数第二题的位置，属于把关题的难度.从阅卷情况来看，第（1）问的得分率为40%，第（2）问的得分率为15%.

讲评记录：第（1）问的方法较多，这里只提一种，如图3，在AC上取一点M，使CM=CF，连接MF.

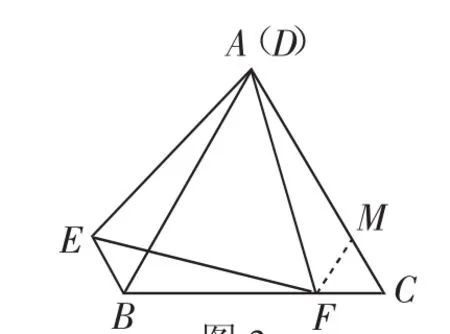
图3

图4

容易得出△CMF是等边三角形，先证明△ABE△ACF，可得到条件有助于证明△BEF △MFA，于是问题获得突破.

对于第（2）问，只要向第（1）问转化就可顺利解决，如图4，过点D作DG//AC，交BC于点G.容易得出等边三角形DBG，这样问题就转化为第（1）问的思路了，这里略去.

为了追求较好的讲评效果，我们还给出了如下的变式跟进.

变式跟进：如图5，等腰直角三角形ABC中，∠A=90°，另一个等腰直角三角形DEF的直角顶点D在射线AB上，顶点F在射线CB上，连接BE.分析线段BE、BD、BF之间的数量关系.

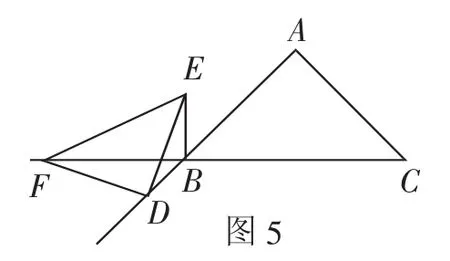
图5

图6

解法预设：如图6，过点D作DG//AC交CB于点G，可得等腰直角三角形BDG，再证明△BDE △GDF，可得BE=GF，从而沟通BG与BD的数量关系，实现问题突破.

还可将图形变式，如图7，点D在边AB上，其余条件不变，仍然可过点D作DG//AC交BC于点G，实现问题解决.

图7

二、七年级几何解题教学的用力点

根据教学观察，不少学生进入八年级就对上述变换类的几何题非常不适应，有些学生直言“第一小问有时还能想到思路，但是图形变式之后就难有思路了”.由此想到不同年级几何解题教学的用力点的相关话题，比如，这种类型问题的解题策略应该在七年级就需要强化训练，也应该是七年级几何解题教学的用力点.以下就结合具体题例的讲评进一步阐述.

考题2：如图8，点P是线段AB上一点，M、N分别是线段AB、AP的中点，若BP=6，求线段MN的长.

教学记录：七年级学习时，不少学生都表示这道试题有点儿难，为了求得较好的讲评效果，我们预设以下一些铺垫式问题.

铺垫问题1：如图9，AB=6，点C是线段AB上一点，M、N分别为AC、BC的中点，求MN的长.

图9

铺垫问题2：如图10，AB=6，点C是线段AB的延长线上一点，M、N分别为AC、BC的中点，求MN的长.

铺垫问题3：如图11，AB=6，点C是线段AB的延长线上一点，M、N分别为AC、BC的中点，求MN的长.

图9

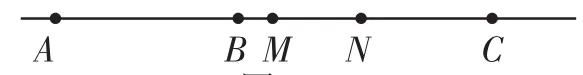
图10

图11

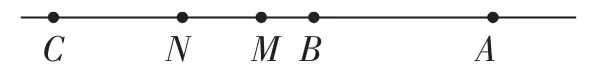
图12

铺垫问题4：如图12，AB=6，点C是线段AB的延长线上一点，M、N分别为AC、BC的中点，求MN的长.

学生理解了图12之后，就可以将字母直接替换成图8中的字母，解题步骤完全相同.

接下来，还可以安排学生继续思考从线段“双中点”到角“双角平分线”变式问题：

变式1：如图13，已知∠AOB=100°，OC是∠AOB内部一条射线，OM、ON分别是∠AOC和∠BOC的平分线.求∠MON的度数.

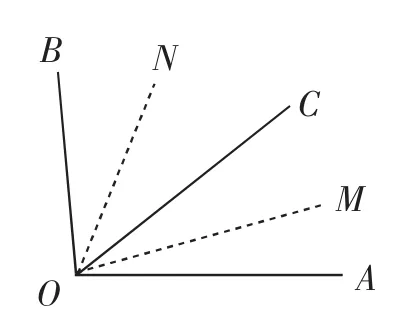
图13

图14

变式2：如图14，已知∠AOB=100°，OC是∠AOB外部一条射线，OM、ON分别是∠AOC和∠BOC的平分线.求∠MON的度数.

让学生把线段的双中点、角的双角平分线放在一起研究，想清辨明“它们都是一样的”，就可以加深对这类问题的理解，对八年级再遇到图形变换之后的全等探究也十分有益.

二、关于几何解题教学的进一步思考

1.七年级起始阶段注重几何语句的组织与规范

学生进入初中阶段有几个关键期.一是有理数初学阶段有理数运算问题中的符号容易出错.第二个关键期就是进入几何学习，几何图形初步学习时，有两大障碍，一是几何符号语言的适应性，以及几何解题语句、解题步骤的组织.不少学生在处理线段、角的计算问题时，常常只有算式而没有几何步骤，这些都是小学阶段几何图形计算问题的解题惯习，需要较长时间的训练才能逐步到位.而几何语句的规范表达又要靠学习几何图形的定义、表示、性质时进行示范，让学生熟记线段中点定义、角平分线定义、互余定义、互补定义等符号表达，灵活运用等式性质、等量代换进行几何语句组织、书写，都是七年级几何初学阶段的训练重点.特别是，像上文提到的线段的双中点、角的双角平分线问题，就不只是简单地停留在会算的层次上，而要让学生学会这些习题的语句表达、详细证明，这样有利于八年级时学习像上文“考题1”这类图形变换问题.

2.八年级几何证题注意图形变换前后的不变性

几何研究图形的形状、大小、位置，也研究图形变换，如平移、旋转、翻折等变换.像上文考题1，由动点引发动形之后相应线段之间的关系也是常见习题.特别是当图形变换之后线段之间、角之间的“变化”或“不变性质”常常是研究的重点与热点问题.对于七年级线段“双中点”距离的不变性质或“双角平分线”夹角的不变性质来说，到了八年级的全等变换之后，三条线段之间的数量关系不一定还是原来的关系，但是证明的思路，特别是辅助线的添加、转化的策略是一样的.这些都需要我们在解题教学时向学生传递、渗透.

3.九年级繁杂线条几何题要善于分离、聚焦图形

九年级的几何学习主要是圆和相似三角形，图形中的线段繁杂，且会将七、八年级特殊三角形、特殊四边形融合在圆中，并且往往涉及相似的探究，所以难度会较大.解题教学时，需要向学生传递渗透分离图形的能力、聚焦图形的意识，前者是提高学生抗干扰的能力，后者是学会识别、善于发现常见图形的能力.比如，圆中垂径定理的相关习题，常常要连接半径、作弦心距等，这些辅助线的主要功能是将问题转化为特殊三角形来研究.再比如，繁杂图形中相似三角形的识别就需较强的分离、聚焦图形的能力，根据条件分析出待证明相似的两个三角形并用阴影表示出来，标注恰当的符号与待证元素之间的关系，为明确解题方向提供帮助.

三、写在后面

代数学习的经验告诉我们，像方程多会有一般形式与非一般形式，求解时往往要将方程化为一般形式以便于进一步解答.而几何的很多求证问题也有类似的一般形式（我们常常称为“标准图形”）和非一般形式（“非标准图形”）.几何证题能力强的学生，往往能在繁杂、难以辨识的“非标准图形”中向“标准图形”转化.想来，这种“一般化”“标准化”的能力也就是我们在数学解题教学过程中的用力点.