灵活应用换元法解决数学问题

☉山东省济南市莱芜区雪野镇中心中学 毕平思

学习了二元一次方程组的解法后，我们知道解二元一次方程组有两种基本方法：代入法和加减法.下面让我们看看如何解方程组根据方程组的特点，常规解法是采用加减法.比较两个未知数的系数，我们发现消去x比较简单，解法如下.①×7，得14x+21y=84③，②×2，得14x-34y=194 ④.③-④，得55y=-110.则y=-2.把y=-2代入①，得2x+3×（-2）=12.则x=9.则原方程组的解为上述解法其实是一种常规解法.本题其实可以应用均值换元法巧解.若实数m、n满足m+n=p，则可设我们称这种换元方法为均值换元法.观察方程①，根据系数特点，可设2x=6+6t，3y=6-6t，即x=3+3t，y=2-2t.代入方程②，得7（3+3t）-17（2-2t）=97.则t=2.则x=3+3×2=9，y=2-2×2=-2.不难发现，采用均值换元法解原方程组，大大减少了运算量，提高了解题效率.实际上，换元法也是一种重要的数学解题方法.在解决数学问题时，有时可以把某个式子看成一个整体，用一个变量去代替它，从而使问题得到简化，叫作换元法.换元法的种类比较多，均值换元法只是其中的一种.应用换元法可以起到化难为易、化繁为简之效，从而提高解题效率.

一、用于计算

分析：由于括号内加数太多，此题若直接计算，无论是先对括号内通分，还是应用乘法分配律，都不现实.注意到括号内有许多相同的项，如可以先将这些相同的项看成一个整体并用字母表示，再计算就方便多了.

解：令则原式

评注：本解法实际上是双参数换元，即在换元时引入两个字母（或参数）.通过换元可以发现，换元之后原式变得非常简捷，而且在计算时相同项可以相互“抵消”.

快乐体验：已知且都是正数，试比较M、N的大小，并说明理由.

二、用于解方程组

分析：本题若按常规解法，需要先对方程组进行化简，比较麻烦，且易出错．若能注意观察到两个方程中都含有可分别视为一个整体，然后运用整体换元的方法求解．

快乐体验：解方程组

例3已知关于x、y的二元一次方程组的解是则关于x、y的二元一次方程组的解是______.

评注：本题若按常规方法，需要将代入方程组①求出再把代入方程组②，得到另一个方程组再解这个方程组，得这样解步骤甚多、运算繁杂，容易产生错误.仔细观察方程组①和②，对比两个方程组的结构.若设x+y=u，x-y=v，则方程组②可变形为方程组③对比方程组①和③，我们发现这两个方程组除了未知数的表达形式不一样，未知数的系数和常数项部分都相同，因此它们的解相同，则即解这个方程组，得显然这样求解非常简捷.

快乐体验：已知方程组的解是则方程组的解是（ ）.

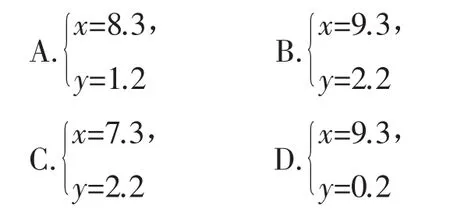
三、用于求二元二次方程的实数解

例4方程x2-xy+y2-x-y+1=0的实数解是_____.

评注：本题若按常规方法，可以先将原方程整理成关于x的一元二次方程，得x2-（y+1）x+（y2-y+1）=0.由方程有实数根的条件，得一元二次方程的判别式即（y-1）2≤0.而（y-1）2≥0，于是（y-1）2=0，则y=1.

将y=1代入原方程，得（x-1）2=0，则x=1.

则原方程的实数解为x=1，y=1.

其实本题若用二元代换求解，非常简捷.由于对于任意实数，恒有令则x=a+b，y=a-b，这种代换就叫作二元代换.二元代换是一种非常重要的换元方法，利用二元代换解决数学问题同样可以起到化繁为简、化难为易之功效.下面利用二元代换解答本题：

则a=1，b=0.则x=1，y=1.

则原方程的实数解为x=1，y=1.

快乐体验：方程x2+xy+y2+x-y+1=0的实数解是_____.

以上仅通过三例说明了换元法在解决数学问题时的作用.换元法的应用还有很多，如我们可以利用换元法解分式方程，如解方程利用换元法解无理方程，如解方程利用换元法解分式方程组，如方程组的解是______（可先对方程组中的每个方程两边分别取倒数，将原方程组变形为的形式，然后再采用换元法）；利用换元法化简分式，如已知：x+y+z=3a（a≠0，且x、y、z不全相等），求的值.希望大家在今后的学习中认真总结，看看哪些数学问题适合应用换元法，并尽可能掌握这种方法，从而提高解决数学问题的效率.W