双拦截弹拦截单目标边界型微分对策制导律研究*
2019-05-22朱东方刘延芳
张 帅,朱东方,孙 俊,华 春,刘延芳
(1. 航空工业哈尔滨飞机工业集团有限责任公司·哈尔滨·150066;2. 上海航天控制技术研究所·上海·201109;3. 上海航天信息研究所·上海·201109;4. 哈尔滨工业大学 航天学院·哈尔滨·150001)
0 引 言
未来的新型空袭武器,如战术弹道导弹(Tactical Ballistic Missile,TBM)、高超声速巡航导弹(Supersonic Cruise Missile,SCM)和无人驾驶飞行器(Unmanned Aerial Vehicle,UAV)等,具有飞行速度快、机动能力强等特点[1]。在拦截这类目标时,拦截弹在速度、机动能力、过载响应速度等方面不再具有明显的优势。同时,由于这类新型目标的结构尺寸小、结构强度高,要对其进行成功拦截需要实现很小的脱靶量,甚至需要通过直接碰撞将其摧毁(Hit to Kill)。
为提高成功拦截的概率,一方面需要采用先进的制导、控制系统,提高单发命中概率(Single Shot Kill Probability,SSKP);另一方面,可以采用同时发射多枚拦截弹的方式完成拦截。本文主要对后者进行了研究。
微分对策理论是在古典对策理论和最优控制理论相结合的基础上,研究双方或多方最优对抗策略的理论[1],其被广泛应用于拦截弹制导律的设计[2-9]。Gutman S 指出,比例导引(Proportional Navigation,PN)制导律是一种在对抗双方都具有理想侧向动力学特性假设下的线性二次型微分对策(Linear Quadratic Differential Game,LQDG)制导律[3],他同时给出了同样假设下、对抗双方控制受限条件下的边界型微分对策(Bounded Differential Game,BDG)制导律[4]。Shinar J等将BDG制导律扩展到了包含拦截弹一阶动力学特性(DGL/0)[5]和目标一阶动力学特性(DGL/1)[6-7]的模型上。考虑对目标状态估计的延迟、速度和速度剖面的时变特性,Shinar J和 Shima T等提出了DGL/C[5,8]、DGL/E[9]和DGL/EC[10]制导律。李云迁等针对新型拦截弹,将复合控制引入到了微分对策制导律中[11-12]。刘延芳等针对大初始航向误差时的角度非线性,提出了非线性微分对策制导律[13]。刘长有等[14]采用强迫奇异摄动给出了非线性微分对策次最优反馈制导律。
然而,以上文献中提出的制导律针对的是一对一拦截问题。在多弹拦截问题中,新拦截弹的加入使得对策模型复杂化,演变为“多对一追踪-逃逸”问题。Perelman A等基于零和(Zero-Sum)理论提出了协同二次型微分对策(Cooperative Linear Quadratic Differential Game,CLQDG)制导律[15-16]。该制导律针对的是航空器通过发射防护导弹来躲避来袭拦截弹攻击的两组三体最优策略问题:拦截弹追踪航空器,航空器躲避来袭拦截弹,防护导弹试图摧毁拦截弹。针对同样的问题,Shima T在攻击导弹采用线性制导律、线性化运动学和完全信息的假设下给出了最优合作追踪-逃逸策略[17]。然而,该问题与多弹拦截问题有很大的不同。彭琛等研究了饱和攻击多弹分布协同末制导问题[18],但此问题并不适用于多弹拦截问题。Foley A M给出了非零和多对一对策问题的基本模型和最优策略[19-20],Lin W给出了在拥有局部信息时的多对一对策问题的纳什平衡策略(Nash Equilibrium Strategy, NESS)[21]。
本文针对两枚拦截弹拦截单目标的末段制导问题,将其建模为非零和二对一追踪-逃逸对策模型,采用微分对策理论给出BDG制导律,并对该制导律的性能进行分析。
1 系统建模
1.1 多弹拦截问题
在末制导段,2枚拦截弹P、Q和目标T的三维相对运动可以分解到2个正交平面内,本文仅对俯仰平面内的运动进行了研究。为简化分析,采用如下假设[1-5,7-8]:
(1)拦截弹和目标的速度为常值;
(2)拦截弹和目标可以获得彼此的精确信息;
(3)拦截弹和目标的相对运动可以在初始视线附近实现线性化;
(4)忽略由于拦截弹和目标高度不同带来的重力加速的影响;
(5)拦截弹和目标的自动驾驶仪具有理想的动力学响应(零阶延迟)。
末制导段俯仰平面内拦截弹和目标间的相对运动如图1所示。其中,V、a和γ分别表示速度、加速度和航迹角;λ和r分别表示视线角和弹目距离;y表示在垂直视线方向上,目标与拦截弹之间的相对距离;下标P、Q和T分别表示拦截弹P、Q和目标T,PT表示P和T之间的对抗,QT表示Q和T之间的对抗,0表示初始时刻。
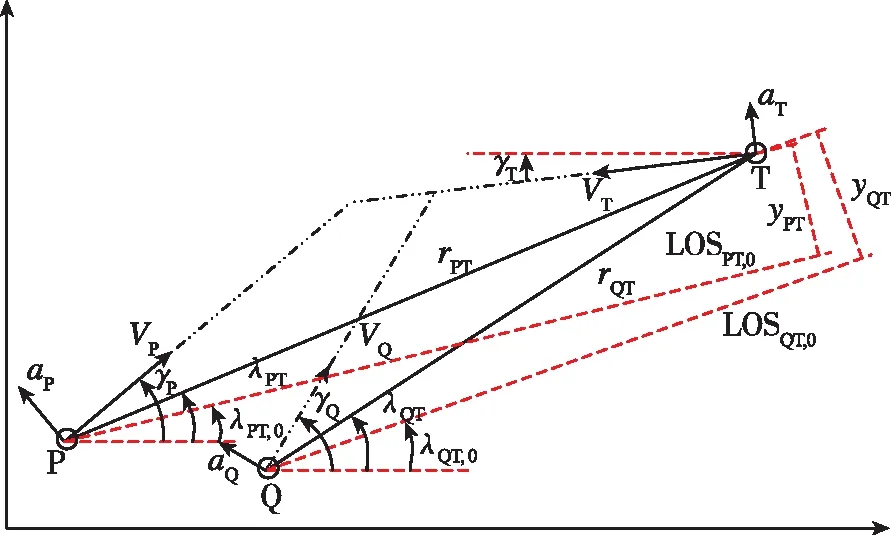
图1 末制导段拦截弹和目标间的几何关系Fig.1 Geometry of end-game guidance
(1)
其中
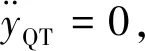
(2)
基于假设1)、3),在给定的初始条件下,对抗PT和QT的结束时间可以近似计算为
(3)
满足
tf,PT>tf,QT
(4)
其中,φ为前置角,定义为
(5)
本文主要对迎向拦截[12]进行研究,对于迎向拦截,前置角满足关系
-π/2<φi<π/2,i∈{P,Q,PT,QT}
(6)
将拦截的结束时间定义为
tf=tf,PT
(7)
拦截弹和目标的最大加速度受限,为避免控制饱和,有
|ui| (8) ZEM表示从当前时刻(拦截弹和目标都不再输出指令时)至末制导结束时的脱靶量的大小。应用状态转移矩阵,ZEM矢量可以表示为 z(t)=DΦ(tf,t)x(t) (9) 其中,状态转移矩阵为 D为常值矩阵,为 将式(9)对时间求导可以得到ZEM动态为 (10) 其中, 假设2枚拦截弹完全一致且拦截过程相互独立,每一枚拦截弹都控制自己的脱靶量使其达到最小,而目标选择使最小脱靶量最大的控制策略,因此拦截弹和目标的目标函数为 (11) 将状态方程(1)、约束方程(8)和目标函数(11)定义的非零和二对一追踪-逃逸对策模型表示为G。 (12) 使三个不等式对所有的容许控制uP、uQ和uT都成立,则该策略集称为G的纳什平衡策略。 由于式(11)中目标的性能函数不连续,为了应用现有理论进行求解,重新定义连续的性能函数为 (13) (14) (15) 协变量满足 (16) 最优控制策略为 (17) 其中 将开环最优策略(15)代入式(9),可得到最优零控脱靶量动态 (18) 定义2:ZEM矢量z(t)的集合称为拦截空间S,即 S={z(t)} (19) 2.2.1 P-拦截空间 定义3:满足 的ZEM矢量组成的拦截空间S的子空间称为P-拦截空间,即有 (20) 定理1:如果满足z(t)∈SP,当κ=1时式(17)是对策模型G的纳什平衡策略。 (21) 因此,为证明式(17)是G的纳什平衡策略,只需要对式(12)中的第三式进行验证。 当κ=1时, (22) 将式(17)代入式(10),可以得到 (23) 由z(t)∈SP,可以得到|zP(tf)|<|zQ(tf)|,因此有 (24) 假设拦截弹P和Q采用式(17)的策略,而目标采用任意容许策略uT,此时有三种可能的结果 a) |zP(tf)|>|zQ(tf)|,此时有 (25) 结合式(22)、(24)和(25),可以得到 (26) 对于情况b)|zP(tf)|=|zQ(tf)|和c)|zP(tf)|<|zQ(tf)|,同样可以得到式(26)成立,即式(12)第三式得到验证。因此,如果满足z(t)∈SP,当κ=1时,式(17)是对策模型G的纳什平衡策略,定理得证。 在P-拦截空间里,结合式(20)和式(23),可以得到 signz(t)=signz(tf) (27) 因此,最优反馈制导律为 (28) 2.2.2 Q-拦截空间 定义4:满足 的由ZEM矢量组成的拦截空间S的子空间称为Q-拦截空间,即有 (29) 定理2:如果满足z(t)∈SQ,当κ=0时,式(17)是对策模型G的纳什平衡策略。 证明:同定理1,这里只需要对式(12)中的第三式进行验证。 当κ=0时, (30) 将式(17)代入式(10),可以得到 (31) 由z(t)∈SQ,可以得到|zP(tf)|>|zQ(tf)|,因此有 (32) 假设拦截弹P和Q采用式(17)的策略,而目标采用任意容许策略,此时有三种可能的结果 a)|zP(tf)|>|zQ(tf)|,此时有 (33) 结合式(30)、(32)和(33),可以得到 (34) 对于情况b)|zP(tf)|=|zQ(tf)|和c)|zP(tf)|<|zQ(tf)|,同样可以得到式(34)成立,即式(12)第三式得到验证。因此,如果满足z(t)∈SQ,当κ=0时,式(17)是对策模型的纳什平衡策略。定理得证。 在Q-拦截空间里,结合式(29)和式(31)可以得到 signz(t)=signz(tf) (35) 因此,最优反馈制导律为 (36) 2.2.3 PQ-拦截空间 定义5:存在0<κ<1使得在式(17)策略的作用下终端零控脱靶量满足zP(tf)=zQ(tf)的拦截空间的子空间称为PQ-拦截空间,即有 SPQ={z(t)|∃0<κ<1,zP(tf)=zQ(tf)} (37) 定理3:如果满足z(t)∈SPQ,当κ满足|zP(tf)|=|zQ(tf)|时,式(17)是对策模型G的纳什平衡策略。 证明:同定理1,这里只需要对式(12)中的第三式进行验证。 根据PQ-拦截空间的定义,当z(t)∈SPQ时,|zP(tf)|=|zQ(tf)|,因此有 (38) 假设拦截弹P和Q采用式(17)的策略,而目标采用任意容许策略uT,此时有三种可能的结果: 情况a)为 |zP(tf)|>|zQ(tf)|,此时有 (39) 结合式(38)和(39),可以得到 (40) 对于情况b)|zP(tf)|=|zQ(tf)|和情况c)|zP(tf)|<|zQ(tf)|,同样可以得到式(40)成立,即式(12)第三式得到验证。因此,如果满足z(t)∈SPQ,当κ满足zP(tf)=zQ(tf)时,式(17)是对策模型G的纳什平衡策略。定理得证。 在PQ-拦截空间里,0<κ<1,根据式(17),当signzP(tf)=signzQ(tf)时,最优反馈制导律为 (41) 当signzP(tf)=-signzQ(tf)时,最优反馈制导律与κ相关,其中κ可通过求解|zP(tf)|=|zQ(tf)|获得。 典型的拦截空间分布如图2所示,其中中心区域为奇异区(Sigular Range),其物理意义将在下一节进行说明。在奇异区,拦截弹和目标的最优反馈策略是任意的。 图2 拦截空间分布Fig.2 Distribution of intercept space 在给定任意最终脱靶量时,结合式(14)可以得到κ值,将κ值带入式(17)可以获得最优制导策略,将最优制导律代入式(18)并积分可以得到最优轨迹。当zP(tf)=zQ(tf)时,取κ值为[0,1]之间任意的数,可以得到给定κ值下的最优轨迹。从不同的最终脱靶量及κ值出发,可以得到最优轨迹集合,该集合填充着对策空间(t,zP,zQ)。典型的对策空间的结构如图3所示。图中给出的曲线为奇异区与P-拦截空间、Q-拦截空间及PQ-拦截空间的边界最优航迹。P-拦截空间、Q-拦截空间和PQ-拦截空间之外的区域为奇异区。当拦截的初始条件位于该区域时,最优导航策略是任意的。不论采用什么样的制导策略,当零控脱靶量矢量达到边界最优航迹时,其会沿着边界最优航迹运动,并保证零脱靶量拦截。从图3可以看到,当P拦截弹和Q拦截弹的初始零控脱靶量具有相反的符号时,奇异区域会增加,即零脱靶量拦截的区域有所增加。 图3 对策空间结构Fig.3 Game space structure 选择在初始ZEM矢量位于PQ-拦截空间条件下进行仿真研究,两枚拦截弹采用本文提出的制导律(表示为LQDG/S),目标采用“棒-棒”机动策略,即初始时沿某一方向采用最大加速度机动,在时刻(tgo)sw时改变机动方向沿相反的方向以最大加速度机动[5,8,10-12]。假设目标无法获得拦截弹的准确信息,加速度方向的改变时间随机,此时目标以一定的概率实现最优机动。在不同的仿真中,机动方向的改变时刻(tgo)sw在剩余飞行时间内以0.03s的时间间隔变化。在仿真中,制导周期为10ms,积分步长为1ms。目标和拦截弹的加速度受最大可用过载的限制。仿真采用的主要参数在表1中给出。 表1 仿真参数 图4、图5给出了(tgo)sw=2s时的零控脱靶量和加速度随时间变化的曲线。图6给出了脱靶量随目标机动方向的转向时间变化关系,图6中的直线表示脱靶量的均值。其中,脱靶量定义为拦截弹P和Q的脱靶量的最小值。从图6可以看到,脱靶量的均值约为0.4m。在目标的加速度转向时间(tgo)sw=0.4s时,脱靶量存在峰值,表明该时刻为目标的最优机动转向时机。 图4 零控脱靶量轨迹Fig.4 Trajectory for zero-effort miss distance 图5 加速度曲线Fig.5 History of acceleration 图6 脱靶量随转向时间的变化曲线Fig.6 Relationship between miss distance and switch time 本文主要研究了2枚拦截弹同时拦截单个目标时在末段制导问题,主要结论为: (1)将2枚拦截弹同时拦截单个目标的问题建模为“非零和二对一微分对策模型”,并采用最优控制及边界型微分对策理论对模型进行求解; (2)拦截空间分解为4个相互交集为空集、且并集覆盖整个拦截空间的子空间SP、SQ、SPQ和奇异区,并根据纳什平衡策略给出了考虑其他拦截弹存在的边界型微分对策制导律; (3)当2枚拦截弹在初始时刻的零控脱靶量具有相反的符号时,对策空间存在一个较大的奇异区; (4)仿真结果表明,采用2枚拦截弹进行拦截时,脱靶量对目标机动方向的转变时间具有很好的鲁棒性。1.2 对策模型

2 纳什平衡策略
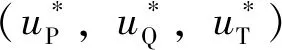
2.1 伴随模型及求解


2.2 拦截空间及最优策略



2.3 对策空间结构
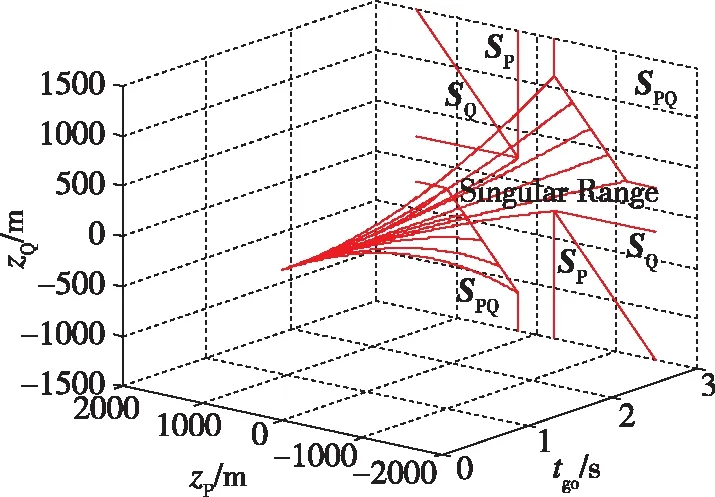
3 仿真研究

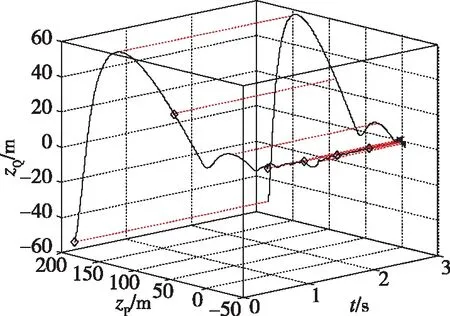
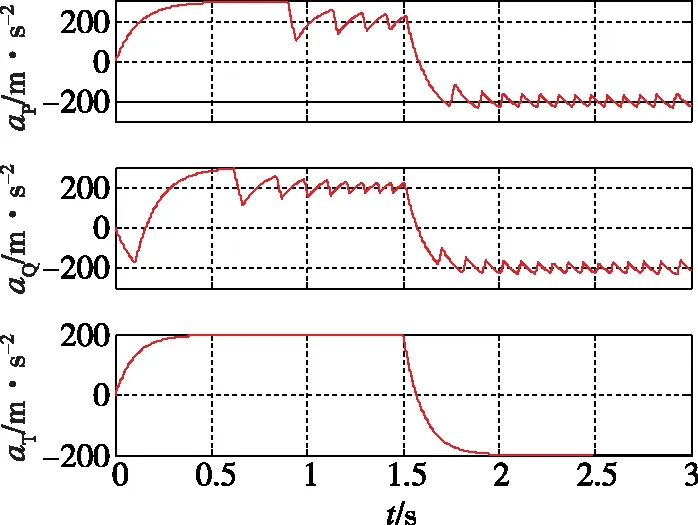

4 结 论
