基于响应面全局优化技术的蜂窝板材料性能参数修正
2019-05-21孙卫青
孙卫青,程 伟
(北京航空航天大学 航空科学与工程学院,北京 100191)
近年来,航天器的微振动问题已经引起越来越多的关注。微振动是由各种扰振源(如动量轮,控制力矩陀螺和太阳能帆板作动器)所激励引起,而后通过航天器的结构传递到成像或指向装置,导致精度降低。微振动的能量分布在1kHz左右的较宽的频率范围内,可能会激发起航天器上某些结构件的弹性体模态,而且这种宽频的振动又无法通过姿态调整系统或轨道控制系统来进行抑制。
对于微振动的控制有两种途径。一方面,国内外有很多学者在研究通过设计无源或有源隔振器来最小化扰振源作用到结构上的载荷。而另一方面,可以通过优化航天器结构,并采用具有高刚度/质量比的材料(例如目前广泛使用的蜂窝夹层板),从而降低传递到最终目标点的振动。
对于蜂窝夹层板结构的动力学特性研究,早在20世纪80年代,基于Mindlin板壳理论,曾经开发出了一些夹层板弯曲振动的理论方法[1-4]。而自20世纪90年代以来,有限元(FE)方法开始广泛应用于结构动力学仿真[5-13]。无论采用何种夹层板结构的动力学分析方法,要想获取准确的分析结果,都首先要保证表层及特别是芯层结构的材料参数是精确的。在上述的一些研究工作中,芯层的材料参数往往都是通过实验测定的。然而,对于一些软芯材料(如蜂窝芯),因为在实验中往往需要通过特别的夹紧装置对其进行固定,因而想要准确地获取其材料参数尤其是面外剪切模量的难度较大。而芯层的面外剪切模量又恰恰对于整体夹层结构的动态特性而言是最为重要的。由于构建详细的芯层有限元模型计算成本较高,因此工程上最有效的方法是基于理论计算构建芯层甚至整个夹层板的等效模型,但是考虑到生产加工过程中的工艺误差,必须对等效模型进行验证和校核。Jiang等[14]曾试图通过模态实验数据对铝蜂窝板的蜂窝芯的面外剪切模量进行修正。Debruyne等[15]通过对模态实验数据及有限元分析结果进行随机性分析,研究了表层蒙皮杨氏模量和蜂窝芯面外剪切模量的变化特性。孔宪仁等[16]曾试图将芯层等效为各向同性材料,建立了材料参数对应蜂窝板固有频率的响应面模型,但并没有通过实验进行有限元模型的有效性验证。总体而言,目前针对这方面的研究工作并不多,而且对于芯层材料等效参数辨识的优化算法研究也不甚完整。
对于航天器的微振动问题,由于其本身具有激励能量小,振动响应级别在微米级别的特点,因此对于有限元模型的精度有更高的要求。
此外,航天器蜂窝板结构中通常有用于装配的预埋件,对于预埋件的处理目前鲜有文献提及。本工作建立了典型航天器蜂窝板带预埋件结构的动力学模型,并考虑了胶层附加质量的影响,尝试使用基于响应面模型的快速全局优化技术对蜂窝板动力学有限元模型进行修正,以满足微振动分析的高精度要求。
1 方法及原理
1.1 双层壁蜂窝芯的等效模型
给定芯层材料的杨氏模量Es,剪切模量Gs,密度ρ及泊松比νs,可以根据以下理论计算双厚度壁六边形蜂窝芯(如图1所示)的等效材料特性参数。

图1 双层壁厚六面体蜂窝芯胞元示意图Fig.1 Sketch of a cell in a hexagonal honeycomb core
首先通过施加单位载荷和单位位移的方法推导出两个方向的面外剪切刚度值G13和G23[17]
(1)
(2)
根据胞元中材料所占的百分比,可以计算得到芯层材料的密度
(3)
考虑蜂窝芯的法向刚度与其密度成正比,得到
(4)
通过在末端施加力矩,然后计算胞壁的弹性变形,获得面内模量和泊松比[18-19]
(5)
(6)
(7)
(8)
(9)
基于上述方程的推导过程,进一步综合考虑了轴向和剪切变形,推导出了精确的面内泊松比[20]
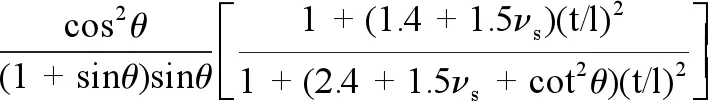
(10)
对于剪切模量G23,可以通过对蜂窝芯单胞进行有限元分析并对比不同高宽比的剪切模量,得到G23的最小二乘回归近似确定值[21]
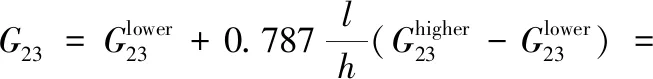
(11)
面外泊松比ν31和ν32等于芯层材料的泊松比,根据互易性关系计算得到ν13和ν23[22]
ν31=ν32=νs
(12)
(13)
(14)
1.2 响应面模型
响应面模型(response surface model, RSM)目前已经在很多领域得以广泛应用[23]。王开山等[24]曾尝试用二阶多项式构建了印制电路板的动力学响应面模型。鲍诺等[25]针对某飞机模型的前10阶模态频率建立了四阶多项式响应面模型。
要得到一个准确的响应面模型,需要预先考虑两个方面:数值分析样本的实验设计方法及构建响应面模型的函数算法。
1.2.1 实验设计方法
实验设计的抽样方法大致可分为两类:正交设计和随机设计。正交设计的优点是所有输入参数在统计学上都是独立的,因此在物理实验中随机误差最小。然而,正交设计总是集中在边界上[26],实验次数将随着输入参量设计值的数量成指数倍数增长,对于高阶响应面模型而言将会大幅提高计算成本。因此,正交设计一般主要用于设计参量筛选,从大量设计变量中识别出最重要的因素[27]。
对于确定性计算分析(包括有限元分析)不存在随机误差,而且随机采样可以最小化设计区域上的累计均方差[28]。目前最常用的随机抽样方法是拉丁超立方体设计方法(Latin hypercube design,LHD)。
图2是中心复合实验设计(central composite ins-cribed design,CCID)和一种LHD对于两个输入参量(X1,X2)的抽样对比。

图2 中心复合实验设计(a)和一种拉丁超立方体实验设计(b)对于两个输入参量的抽样对比Fig.2 Sample points for two input factors of CCID(a) and a possible LHD(b)
1.2.2 响应面模型构建算法
最常用的响应面模型构建算法包括多项式回归算法、Kriging算法和径向基函数(RBF)等算法。Jin等[29]通过比较不同模型对于具有不同问题尺度,不同程度非线性和噪声的问题所获得的结果,认为在大多数情况下,RBF是在准确度和鲁棒性方面最可靠的方法,特别是对于高阶非线性问题而言。
RBF模型的基函数以采样数据点和待预测点之间的欧几里德距离为变量,这样可以保证RBF模型在所有采样点位置的函数值等于采样数据的输出响应。RBF模型的一般形式是
(15)
(16)
其中βi是加权因子,ri表示输入向量和第i次实验设计点之间的欧几里德距离,φ(r)是欧几里德距离函数,其中最为普遍的函数形式包括以下4种:
(1)线性函数:φ(r)=rφ(r)=r
(2)立方函数:φ(r)=r3
(3)薄板样条:φ(r)=r2lg(r)
基于实验样本,方程(15)可以以矩阵形式写成
Aβ=y
(17)
其中,

(18)
β=(β1,…,βn)T
(19)
y=(y(1),…,y(n))T
(20)
通过线性方程组求解来,可以确定得到各加权因子βi(i= 1,…,n)
β=A-1y
(21)
构造RBF模型完成后,就可以模拟输入参数空间内任意点x的输出
(22)
1.3 基于响应面模型的优化算法
基于响应面模型的优化算法是一种基于响应面模型进行自适应采样的全局优化算法。Jones等[30]最早提出了基于Kriging响应面模型进行自适应LHD采样进行全局优化的方法,其原理如图3所示。首先使用基于LHD采样的少数几个样本来初步探索设计空间,然后建立初步的响应面模型,根据得到的响应面模型分析可能的最优区域,在该区域中逐步添加新的样本,并不断更新响应面模型。重复该过程,直到新的采样点非常接近现有采样点之一。优化终止条件通常可以定义为新采样点与现有采样点间的距离容差,即当新采样点与现有采样点的距离相对现有采样点空间坐标的百分比小于该容差限值时,优化终止。
评估添加新样本的可能最优区域主要基于两方面的考虑:(1)响应面模型是否能够预测到更好的设计;(2)在该区域内的样本数是否太少以至于响应面模型在该区域的准确性无法保证。因为这种优化算法仅基于自适应采样,相比较遗传基因等全局优化算法的迭代过程,可以充分保证其效率。

图3 基于响应面模型的优化算法流程图Fig.3 Efficient global optimization work flow for response surface modal
2 实验及有限元建模
图4所示的蜂窝夹心板结构中,面板和芯层材料均为铝合金(材料特性如表1所示)。根据式(1)~(14)计算得到蜂窝芯的等效材料性能(如表2所示)。

图4 蜂窝板尺寸示意图Fig.4 Schematic diagram of honeycomb plate

Young’s modulus,E/GPaDensity, ρ/(kg·m-3)Poissonratio,ν69 2730 0.33
如图5所示,通过锤击法模态实验测量夹层板的动态响应特性。被测蜂窝板用软橡胶带悬挂以模拟自由边界条件。总共有56个敲击点(7×8)和1个加速度响应点,带宽设置为2kHz,频率分辨率为0.5Hz。相关测试设备列于表3中。

表2 蜂窝芯等效材料特性参数Table 2 Equivalent material properties of the honeycomb core

图5 蜂窝板动态响应实验示意图Fig.5 Test set-up of dynamic response experiment for the honeycomb plate

表3 模态测试设备列表Table 3 Measurement devices employed for modal testing
使用Nastran以壳-实体-壳(shell-volume-shell,SVS)的方式进行蜂窝板建模,其中两个面板使用壳单元,芯层使用实体单元。整个模型包含5376个实体单元和2层共5376个壳单元。
对于用于螺栓连接的铝材质预埋件,在模型中处理为分布式集中质量添加到对应的芯层实体节点上。在整个蜂窝板中有两种预埋件,两个垂直边上有12个大预埋件,每个质量为0.0405kg,两个水平边上有14个小预埋件,每个质量为0.0183kg。胶层的附加质量影响也作为分布式集中质量附加到两层面板的壳单元节点上。胶层的质量由整板实际质量减去铝蜂窝芯、两个铝面板及预埋件质量而计算得到,总质量为0.60kg。
表4为通过有限元分析获得的1kHz带宽内前6个模态频率与实验结果的对比。各阶模态的模态置信准则(MAC)值均大于0.9,最大频率误差不超过3%,平均误差为1.24%。说明有限元分析结果与实验结果吻合较好。但对于第1阶、第2阶以及第5阶模态,误差在1%~3%之间,可期待通过模型修正进一步提高其精度。
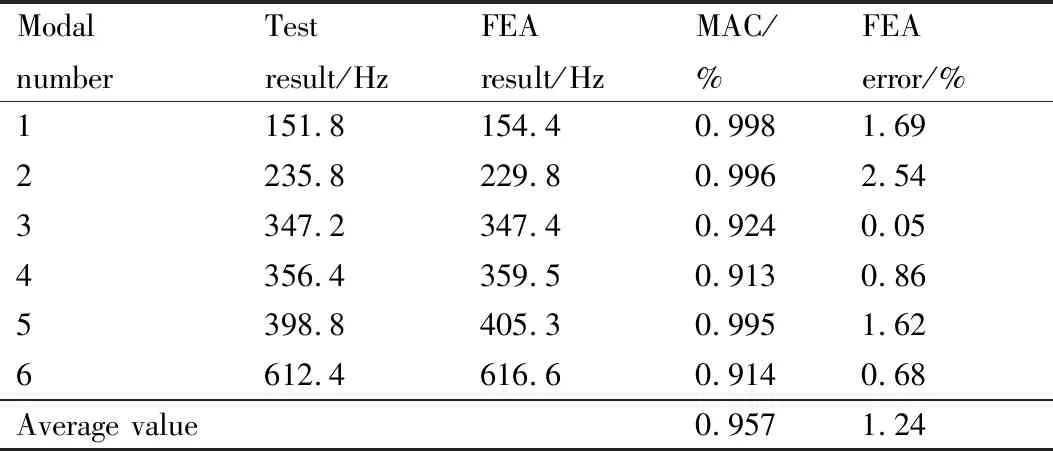
表4 初始有限元模型分析结果与实验结果模态频率对比Table 4 Modal frequencies from the FE analysis and experimental results
3 有限元模型修正
3.1 识别用于优化的输入参数
在进行有限元模型修正之前,首先需要确定待优化参数。对于蜂窝板蒙皮的材料参数、预埋件及胶层的质量均可认为是确定的。考虑到蜂窝板加工工艺的误差,应将蜂窝芯理论等效模型的材料属性作为待优化参数。
蜂窝芯属于正交异性材料,对应Nastran实体单元CHEXS,需要将蜂窝芯的正交各向异性材料参数根据胡克定律转移为MAT9的各向异性材料参数矩阵。即将6个材料参数(E11,E22,E33,G12,G23,G31)和ρ转化到6×6的MAT9材料参数矩阵D中,矩阵D中8个有效元素与6个材料参数的对应关系为:d11=(1-ν23ν32)/(E22E33Δ),d12=d21=(ν12+ν13ν32)/(E11E33Δ),d13=d31=(ν31+ν21ν32)/(E22E33Δ),d22=(1-ν13ν31)/(E11E33Δ),d33=(1-ν12ν21)/(E11E22Δ),d44=G12,d55=G23,d66=G31,其中Δ=(1-ν12ν21-ν23ν32-ν31ν13-2ν12ν23ν31)/(E11E22E33),其他元素均为零。
鉴于输入参量相对较多,为提高优化效率,可以首先确定出仿真模型对哪些输入参数最为敏感,哪些是最为重要的输入参数,以缩减优化变量的个数。
利用1.2节中提到的正交实验设计中的中心复合实验设计(CCID)进行计算,然后根据计算产生的样本进行Pearson相关分析,可以确定出最重要的输入参数。
输出结果(y)和第k个输入参数(xk)之间的Pearson相关系数rk定义为:
(23)

Pearson相关系数取值在-1和+1之间。接近+1或-1意味着该输入参数对分析结果存在直接的正向或反向影响,而接近0表示这个输入参数与分析结果之间相对独立。相关性分析的样本能够覆盖整个设计空间,因此它可以反映每个输入因子对结果的总体影响。
表5列出了各输入参量对应各阶固有频率的相关系数。图6对比了各参量对六阶模态频率的平均相关系数,可以确定出d55(G23),d66(G31)和ρ是3个最重要的参数。
3.2 基于响应面模型的优化
根据相关性分析的结果,选择蜂窝芯的3个等效材料参数(G23,G31和ρ)作为进一步优化的输入参数,将有限元分析和实验结果的前六阶模态频率的平均误差作为最小化目标函数:

表5 蜂窝芯材料参数对应各阶模态的Pearson相关系数Table 5 Correlation factors of the honeycomb core material parameters for each modal frequency
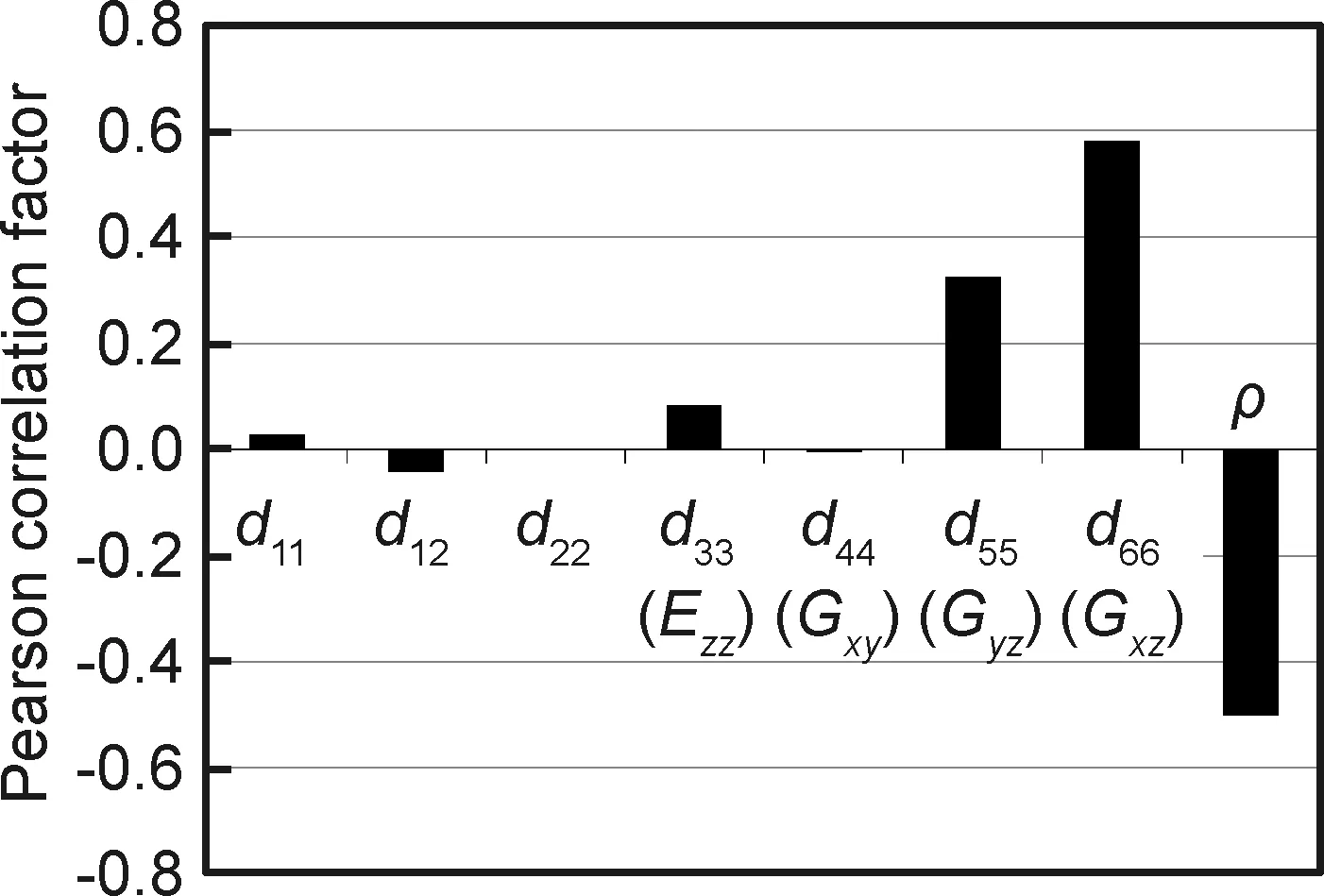
图6 蜂窝芯各材料参数与六阶模态频率的平均相关系数Fig.6 Averaged correlation factors for the six modal frequencies
(24)
其中λi是各阶模态特征频率,下标i是模态阶数。
使用径向基函数响应面模型进行自适应拉丁超立方采样,进行全局优化。径向基函数采用立方函数,每次迭代的采样点数为10。优化终止条件中新采样点与现有采样点的距离容差设为0.1%。图7为整个迭代过程中的采样点分布,其中不同颜色代表密度的大小(范围为20~35kg/m3),圆的直径尺寸代表频率误差的大小(范围为0.88%~22.24%),从图7中可以看到当G23= 130MPa,G31= 91MPa附近优化过程得以收敛。整个优化过程仅用了22次计算即到了输入参数最优解(见表6)。

图7 基于径向基函数响应面模型的全局优化采样点分布Fig.7 Samples distribution during global optimization based on RBF response surface model

表6 蜂窝芯等效材料特性参数优化结果Table 6 Optimization results of equivalent material property of the honeycomb core
表7为修正后有限元模型的模态频率与实验结果的对比,图8为初始有限元模型和修正后有限元模型的模态频率精度对比。从中可以看出除第3阶,其他各阶分析精度相比较初始有限元模型均得以提高,平均频率误差从1.24%降低为0.88%。而第3阶模态误差尽管略有所放大,但精度仍可控制在0.15%,相比较其他阶,尤其是第4阶和第5阶模态精度的改善,是可以接受的。
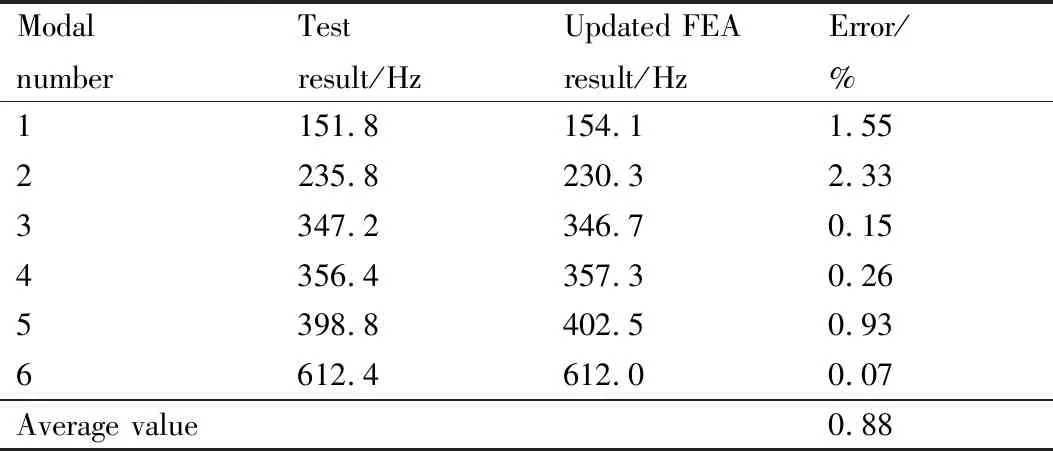
表7 修正后有限元模型结果与实验结果的模态频率对比Table 7 Modal frequencies from the updated FE analysis and experimental results
图9为当密度为23.58 kg/m3时,G23和G31相对模态频率平均误差的响应面模型。图9中可以看出,当2个面外剪切模量G23和G31取值分别超过100MPa和70MPa后,平均频率误差精度逐渐稳定,逐渐逼近最优点。

图8 初始和修正后有限元模型的模态频率精度对比Fig.8 Modal frequencies error comparison between initiative and updated FE model

图9 G23和G31相对6阶平均模态频率误差的响应面 模型(ρ=23.58kg/m3)Fig.9 Response surface model ofG23andG31for average error of first six modal frequencies (ρ=23.58kg/m3)
4 结论
(1)基于蜂窝夹层板的蜂窝芯等效参数模型,建立了考虑安装预埋件及胶层附加质量的铝蜂窝夹层板有限元模型。
(2)通过正交数值实验设计(中心复合实验设计)从蜂窝芯层的9个等效材料参数中筛选出3个重要参数作为有限元模型修正的输入参量。
(3)利用基于响应面模型的全局优化技术对蜂窝芯的两个面外剪切模量及密度进行了参数优化,修正后的有限元模型的前六阶模态的平均频率误差达到0.88%,最大误差不超过2.5%,精度可以满足航天器微振动分析的要求。
