县域中小企业生命周期研究

姚健琪，杨云波，施建华，陈晓平

（1.福建师范大学 数学与信息学院，福建 福州350117;2.闽南师范大学 数学与统计学院，福建 漳州363000）

随着改革开放的步伐，我国中小企业不断地发展，已经逐渐成为国民经济的重要组成部分。然而，中小企业在成长和发展过程中，也面临着一系列发展问题，尤其是生存问题，日益成为社会、政府和学界关注的焦点。劳动力成本上升、出口贸易的同比增加幅度下滑等现象直接影响了我国中小企业健康发展。国内外研究表明，中小企业死亡率高，生命周期普遍较短。Abdesselam 等(2004)发现欧洲中小企业能够生存3年以上的仅占65%，其中能够生存5 a 以上的仅占50%；美国中小企业能够生存5 a 以上的仅占68%，能够生存6～10 a 的约占19%，生存时间超过10 a 的仅占13%；法国中小企业50%以上的生存时间不超过5 a[1]。陈晓红等(2009)对我国五个城市(郑州、成都、长沙、广州、深圳)的中小企业进行统计研究分析，发现这些地区中小企业的平均生存时间为4.32 a，并且这些中小企业存活时间小于3年的占42.99%，存活时间为3～5 a 的仅占26.48%[2]。

国内学者对中小企业生存及其影响因素进行了大量的理论研究和实证分析。张静等(2013)基于1999-2007年我国制造业企业微观数据，阐述了新建公司进入与退出市场的现状，进而利用Cox 比例风险模型探讨了对企业生存有显著影响的因素[3]；何平(2008)搜集并总结梳理了国内外现有关于企业寿命研究的理论成果，提出了延长企业寿命的建议[4]。郑建贞等(2014)利用生存分析模型对中国企业OFDI 持续时间数据进行全样本和分层研究，采用Kaplan-Meier 估计方法分析了中国企业子公司在海外领域的生存时间，应用Cox 模型探讨了对OFDI 生存时间存在显著影响的相关变量[5]。国内外对中小企业的研究中，大多数考虑中小企业发展受融资困难、税收等经济、政策因素的影响，却很少学者对中小企业的发展状态和生存状况进行研究，因此文中以县域中小企业为样本，运用多种分类预测模型，有效地预测县域中小企业的生存状态，最终选取了更有效的logistic 回归模型。

以福建省罗源县工商局1979-2017年登记注册成立的中小企业为研究对象，定义企业注销或者吊销营业执照的时间为死亡时间。截至2017年，1219 家企业注(吊)销，即可知35.15%的企业真实生存时间；而2 249 家企业未注(吊)销，无法得知这64.85%的企业真实生存时间，即出现了右删失数据，这种情况导致数据信息的缺失。由于其含有数据信息，故在对右删失数据进行分析时需要保留未死亡部分，不能直接删除。文中研究的企业生存时间存在删失观测数据的情况，不能直接采用线性回归的方法，故需建立Logistic 回归模型、决策树分类模型和K 近邻分类模型来预测县域中小企业的生存状态，并以误判率和ROC 曲线作为评价标准，将Logistic 回归、决策树和K 近邻分类模型的预测效果进行对比，得出Logistic 回归模型可以更有效地预测县域中小企业的生存状况。

1 数据样本及其处理

文中以罗源县1979-2017年成立的中小企业作为样本数据。企业样本数据包含产业类别、企业类型、企业类别、注册资本。将产业类别和企业类型进一步划分，将产业类别划分为三大产业(第一产业、第二产业、第三产业)，将企业类型划分为五个类别(国有企业、股份合作制企业、集体所有制企业、有限责任公司、其他企业)。以观察期为界限，计算生存时间，为了更好地处理数据和建立模型，将注册资本加1 之后取自然对数。由于抽取的样本有些数据信息不全，故文中剔除了缺失数据。经过预处理之后的样本数据结构见表1。

表1 变量及其类型

2 研究的理论与方法

2.1 logistic 回归模型

逻辑回归是在线性回归的基础上，套用了一个逻辑函数。设因变量Yi是一个二分类变量，取值为1 或0，在m 个自变量影响下发生Yi=1 的条件概率为pi，pi=P（Yi=1∣X1，X1，…，Xm），则Logistic 回归模型[6]的基本结构为：

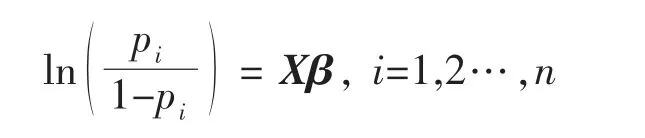
其中β为系数向量，X=（1，X1，X1，…，Xm），β=（β0，β1，…，βp）T。

2.2 决策树模型

决策树模型是一种简单易用的非参数分类器，是基于变量特征对实例进行分类，结构呈树形，由结点和有向边构成。它不需要对数据进行任何的先验假设，计算速度较快，结果容易解释，而且稳健性强。基于ID3 算法和C4.5 算法，决策树学习的主要环节是特征选择、生成决策树、减枝，对训练集样本进行学习时，在损失函数最小的前提下，构建决策树模型，并在决策树模型上对测试集数据进行分类[7]。决策树的一个重要概念是熵，熵表示随机变量不确定性的度量，设X 为一个取有限个值的离散型随机变量，概率分布为：

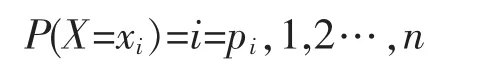
则X 的熵定义为:

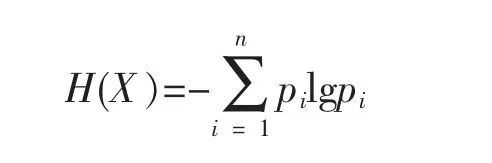
熵越大，随机变量的不确定性就越大。

条件熵H(Y|X)表示在已知随机变量X 的条件下随机变量Y 的不确定性。定义为X 给定条件下Y 的条件概率分布的熵对X 的数学期望

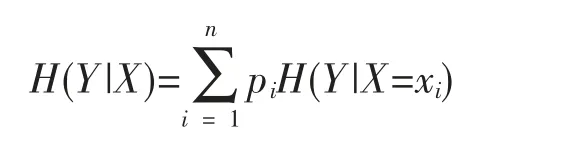
信息增益表示得知特征X 的信息而使得类Y 的信息不确定性减少的程度。特征A 对训练数据集D 的信息增益g(D,A)，定义为集合D 的经验熵H(D)与特征A 给定条件下的经验条件熵H(D|A)之差，即

决策树模型应用信息增益准则来选择特征，通过图解方式求解在不同条件下各类方案的信息增益，然后通过比较，做出决策。信息增益大的特征具有更强的分类能力。

2.3 K 近邻分类模型

K 近邻分类模型是一种目前在回归、分类和模式识别等领域被广泛使用的经典非参数分类模型。

K 近邻分类的基本思想是：给定数据库样本x，需要将它分类,从训练集中找出k 个与其最相近的样本，然后看这k 个样本中哪个类别的样本多，则待判定的值就属于这个类别。k 近邻模型的3 个基本要素是距离度量、k 值的选择、分类决策规则。k 近邻分类模型的基本步骤是：①计算已知类别训练集样本数据中每个点与当前点的距离，一般采用欧氏距离。②根据计算出来的距离，选取与当前点距离最小的k 个点，采用这k 个训练数据样本所属的类别作为样本x 的备选类别。③统计前k个点中每个类别的样本出现的频率， 返回前k 个点出现频率最高的类别作为当前点的预测分类。k近邻分类的核心就是使用一种距离度量，获得距离目标点最近的k 个点，根据分类决策规则，决定目标点的分类[8]。

3 分类预测模型

3.1 Logistic回归模型

3.1.1 变量筛选

若注册资本（X1）、产业类别（X2）、企业类别（X3）、企业类型（X4）为4 维协变量，则logistic 回归模型为：

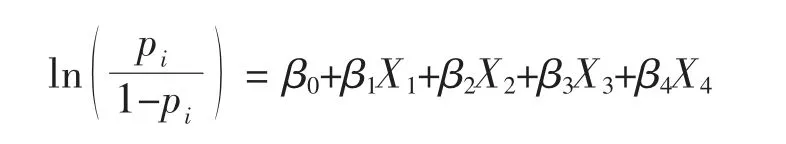
利用AIC 最小准则的逐步回归法选择协变量，其思想是在模型中一次剔除或加入一个协变量，选择AIC 值最小的模型，重复上述操作，直到没有协变量可以被剔除或加入为止，这样得到的最终模型为最优模型[9]。利用AIC 最小准则对上述4 个协变量进行选择，发现全模型AIC 值最小，故全模型为最优模型。则经过变量筛选后的logistic 回归模型为：

3.1.2 Logistic 回归模型的建立

根据变量筛选得到的4 维协变量，由于产业类别(X2)、企业类别(X3)、企业类型（X4）是定性变量，故引入2 个0～1 型自变量X21、X22，反映产业类别的3 个水平；引入2 个0～1 型自变量X31、X32，反映企业类别的3 个水平；引入4 个0～1 型自变量X41、X42、X43、X44，反映企业类型的5 个水平。在全部样本中抽取75%的样本数据作为训练集，25%的样本数据作为测试集， 利用训练集对4 维协变量建立logistic 回归模型，参数β 的估计值如表2所示。将的估计值代入上述模型中，结果如下所示：

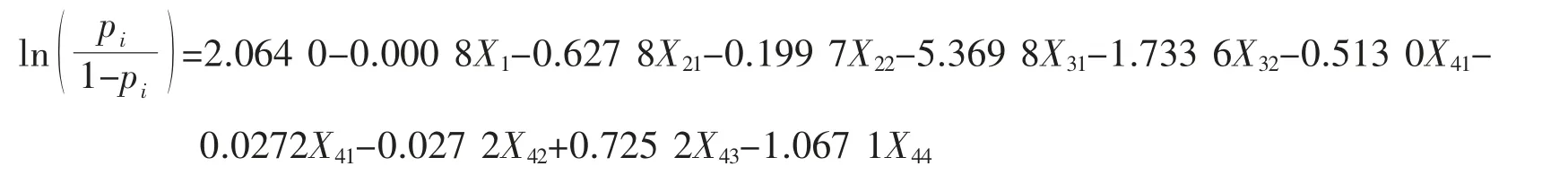
其中X1为注册资本 （对数），

表2 协变量系数及显著性

上述模型结果显示残差为2 400.5， AIC 值为2 420.5，散布参数的估计为1,说明模型未发生过散布现象。

3.2 决策树分类模型

3.2.1 决策树模型的建立

在全部样本中抽取75%的样本数据作为训练集，25%的样本数据作为测试集， 利用训练集样本数据建立决策树分类模型，再用测试集样本数据对该模型进行预测，画出决策树模型图如图1所示。

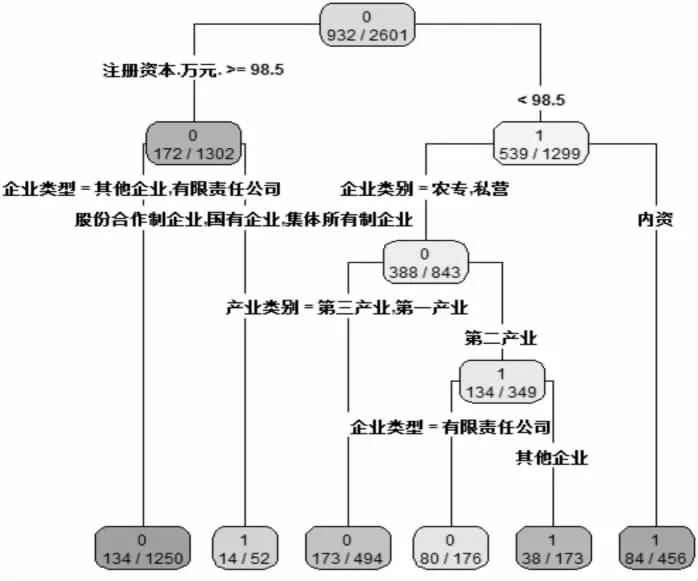
图1 决策树模型图

3.2.2 模型规则提取

利用R 语言提取决策树模型规则，最终提取的规则包含如下6 个。

规则1：当注册资本小于98.5 万元，且企业类别为内资时，判定公司为死亡。

规则2：当注册资本小于98.5 万元，企业类别为农专或私营，产业类别为第二产业，且企业类型为其他企业时，判定公司为死亡。

规则3：当注册资本大于等于98.5 万元，且企业类型为股份合作制企业、国有企业或集体所有制企业时，判定公司为死亡。

规则4：当注册资本小于98.5 万元，企业类别为农专或私营，产业类别为第二产业，且企业类型为有限责任公司时，判定公司为未发生死亡。

规则5：当注册资本小于98.5 万元，企业类别为农专或私营，且产业类别为第一产业或第三产业，判定公司为未发生死亡。

规则6：当注册资本大于等于98.5 万元，且企业类型为有限责任公司或其他企业，判定公司为未发生死亡。

3.2.3 变量重要性

如图2所示，在决策树模型的4 个变量中，最重要的变量是注册资本，其次是企业类型，然后是企业类别，最后是产业类别。

3.3 K 近邻分类模型

在全部样本中抽取75%的样本数据作为训练集，25%的样本数据作为测试集。K 近邻分类3 个重要的 过程是k 值的选取、距离的度量方式和分类决策办法[10]。

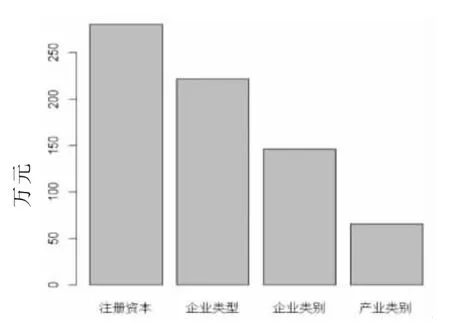
图2 决策树模型的变量重要性图

3.3.1 k 值的选取

利用R 语言建立k 近邻分类算法， 并找出使得测试集误判率最小的k 值，图3是k 值为1到100 时对应的误判率之间的散点图。

由图3可以看出，当k 值取23 时，误判率最低，预测分类效果最好，故23 是最佳k 值。

3.3.2 距离的度量

一般情况下，样本之间的近邻距离是依据欧式距离决定的，故文中采用的距离度量方式是欧氏距离。假设数据集中第i 个样本的特征向量，其中xij表示第i 个样本中第j 个特征的取值。此时任意两个样本xj和xk之间的欧式距离定义为d（xj，xk），公式为：

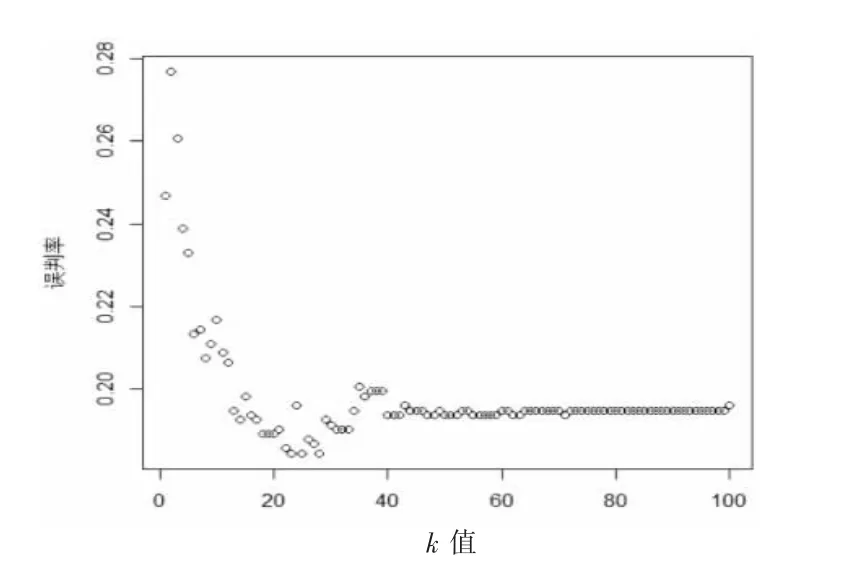
图3 不同k 值的分类效果散点图

3.3.3 分类决策规则

k 近邻分类最常采用的分类决策的办法是多数表决，故文中也采用多数表决的方法确定待分类样本的类别，即哪个类别的样本数目最多，就把样本x 的类别归于哪一类。

4 模型对比

利用测试集的样本，以误判率和ROC 曲线作为评价标准，将logistic 回归、决策树和K 近邻分类模型的预测效果进行对比。

4.1 模型评价标准

4.1.1 误判率

对一般分类模型而言，如果因变量有C 种类别，当C＞1 时，可以通过绘制C*C 错误分类表来评价模型的预测效果及准确性。若pij表示把第i 种类别误判为第j 种类别的个数，则

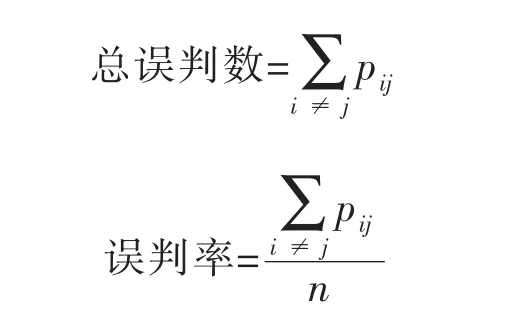
4.1.2 ROC 曲线

ROC 曲线是依据大小不等的阈值，以灵敏度为纵坐标、1-特异性为横坐标描述分类模型预测效果的曲线。由训练集样本建立的模型，给定一个阈值，则可以判断公司是否发生死亡，判断的情况有以下4 种情况：

（1）公司预测结果为未发生死亡，观测值也是未发生死亡，这种情况为真阴性，用TN 表示；

（2）公司预测结果为未发生死亡，观测值为死亡，这种情况为假阴性，用FN 表示；

（3）公司预测结果为死亡，观测值也是死亡，这种情况为真阳性，用TP 表示；

（4）公司预测结果为死亡，观测值是未发生死亡，这种情况为假阳性，用FP 表示。

ROC 曲线纵坐标为灵敏度，也叫真阳性率，sensitivity=TP/(TP+FN)，表示给定阈值时正确预测为死亡的公司个数占真正发生死亡的公司个数的比例。特异性表示给定阈值时正确预测为未发生死亡的公司数占真正未发生死亡的公司个数的比例，ROC 曲线横坐标为1-特异性，也叫假阳性率，1-specificity=FP/(FP+TN)， 表示给定阈值时将未发生死亡错误预测为发生死亡的公司数占真正未发生死亡的公司个数的比例。ROC 曲线描述的是当阈值从0 到1 变动时灵敏度和(1-特异性)之间的关系。AUC 是ROC 曲线下整个区域面积的比重，AUC 常用来评估模型的性能好坏，AUC 的值越大，说明模型越有效，有效的模型在ROC 曲线下方有更大的面积[11]，相应的AUC 的值也越接于1。

4.2 模型测试

运用上文两种评价标准比较Logistic 回归模型、决策树模型和K 近邻分类模型这三种模型的性能。在全部样本中抽取75%的数据作为训练集， 25%的数据作为测试集，用测试集样本数据对利用训练集建立的模型进行测试，这样得出的结论更有说服力。

4.2.1 Logistic 回归模型测试

通过训练集建立Logistic 回归模型，用测试集进行测试，对于每一个测试样本(比如)，利用建立好的模型预测出来的是pi，并不是第i 个样本的预测水平(“0”或者“1”,“no”或者“yes”,等)，此时需要取一个阈值pt，当pi＞pt时，这个测试样本被判定为某一水平；否则被归为另一个水平。

当阈值为0.5 时，可以得到其错误分类表(如表3所示)，这说明有76 个样本原来是水平“0”被误判为水平“1”，有98 个样本原来是水平“1”被误判为水平“0”，正确分类的样本是表中对角线上的样本，此时误判率为0.200692。

显然，用阈值为0.5 不一定合适，应利用R 语言继续找出使得测试集误判率最小的阈值，图4是阈值为0.01 到0.99 时对应的误判率之间的散点图。

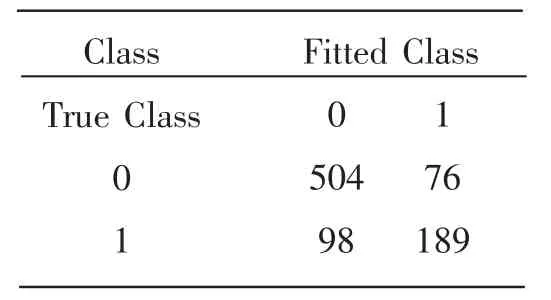
表3 Logistic 回归的错误分类表

图4 不同阈值的分类效果散点图

由图4可知，选择阈值等于0.71，可使得logistic 模型的误判率最小，表4为logistic 回归模型的错误分类表，这说明有41 个样本原来是水平“0”被误判为水平“1”，有117 个样本原来是水平“1”被误判为水平“0”，正确分类的样本是表中对角线上的样本，此时得到误判率为0.1822，阈值为0.71 的效果比阈值为0.5 要好一些。

logistic 回归模型预测的ROC 曲线如图5所示，ROC 曲线下方的面积占整个区域面积的0.8257,所以其AUC 为0.8257，说明logistic 回归模型有很好的预测效果。

4.2.2 决策树模型测试

利用训练集样本建立决策树模型，用测试集样本进行测试，表5为决策树模型的错误分类表，这说明有53 个样本原来是水平“0”被误判为水平“1”，有113 个样本原来是水平“1”被误判为水平“0”，正确分类的样本是表中对角线上的样本，此时可以得到误判率为0.1915。

决策树模型预测的ROC 曲线如图6所示，ROC 曲线下方的面积占整个区域面积的0.7574,所以其AUC 为0.7574，从误判率和AUC 来看，无论是分类的判别还是敏感度，决策树模型都不如logistic回归。

表4 Logistic 回归的错误分类表

表5 决策树的错误分类表

图5 logistic 回归测试样本的ROC 曲线

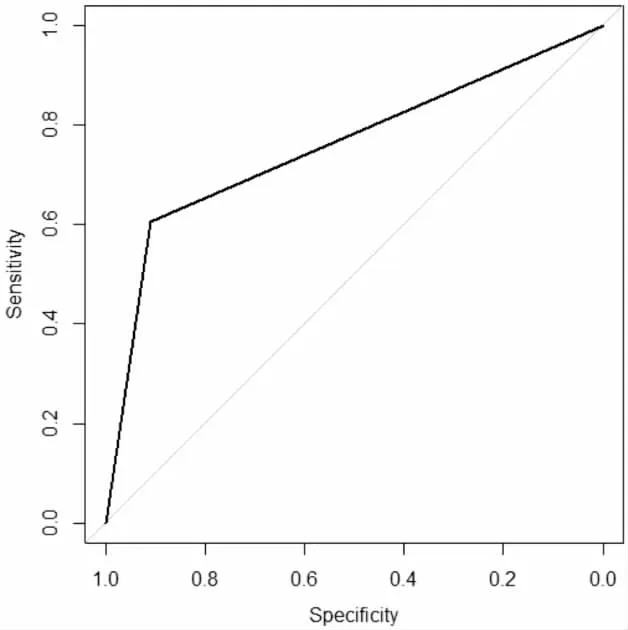
图6 决策树模型测试样本的ROC 曲线

4.2.3 k 近邻分类测试

由上文可知，选择k 值等于23，可使得k 近邻的误判率最小，表6为k 近邻模型的错误分类表，这说明有56 个样本原来是水平“0”被误判为水平“1”，有104 个样本原来是水平“1”被误判为水平“0”，正确分类的样本是表中对角线上的样本，此时得到误判率为0.1845。

k 近邻分类模型预测的ROC 曲线如图7所示，ROC 曲线下方的面积占整个区域面积的0.7705,所以其AUC 为0.7705，说明k 近邻分类模型有不错的预测效果。

表6 k 近邻的错误分类表

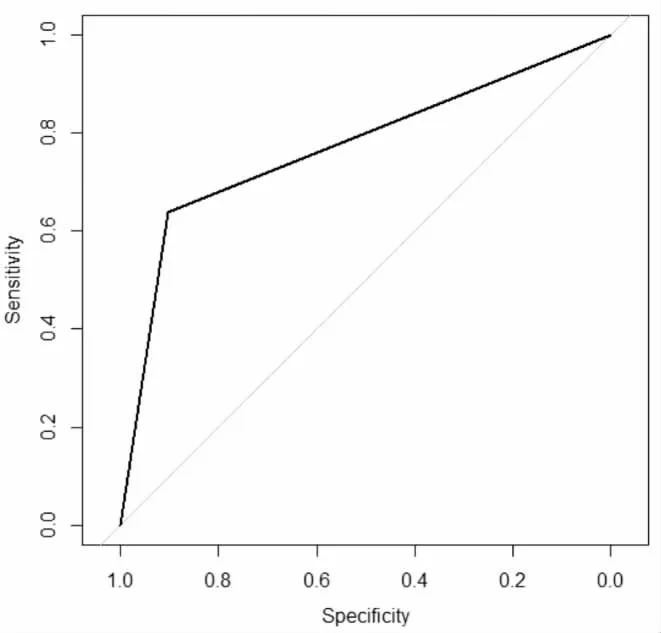
图7 k 近邻分类模型测试样本的ROC 曲线

4.3 模型比较

介绍二个常用的评价模型性能的标准， 即误判率和ROC 曲线。用训练集样本分别建立了Logistic 回归模型、决策树模型和k 近邻分类模型，并计算了各个模型的误判率和AUC 值，表7是这3种分类模型预测效果汇总表。从误判率来看，决策树模型的误判率最大，k 近邻分类模型的误判率次之，Logistic 回归模型误判率最小；从AUC 来看，logistic 回归模型的AUC 值最大，k 近邻分类模型的AUC 值次之，决策树模型的AUC 值最小。从误判率和ROC 曲线两个常用的评价模型性能的标准来看，基于Logistic 回归的分类预测模型误判率最低，AUC 值最大，预测正确率最高，说明基于Logistic回归的分类预测模型可以有效地预测企业发生死亡情况。同时，3 个模型的AUC 值均大于0.5，由此说明三者都可以预测企业发生死亡情况。

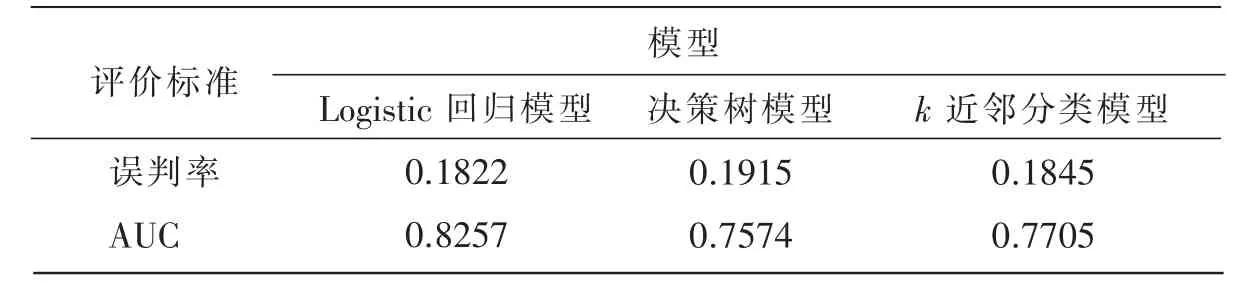
表7 3 种分类模型预测效果汇总表

5 结论与政策建议

以罗源县中小企业为样本，利用所抽取的训练集样本分别建立logistic 回归模型、决策树分类模型和k 近邻分类模型来分析对中小企业生存周期有影响的因素， 并以误判率和ROC 曲线作为模型性能的评价标准，将Logistic 回归、决策树和K 近邻分类模型的预测效果进行对比。主要结论有：①注册资本、产业类别、企业类别和企业类型对企业的生存周期存在显著影响且在不同时间段内生存概率存在显著差异。②企业注册资本越高，企业生存时间越长；第三产业的企业生存时间更长；国有企业比其他四种企业生存时间更长；农专的生存概率最高，内资企业的生存概率最低。③在这三个模型中，基于logistic 回归的分类预测模型误判率最低，AUC 值最大，预测正确率最高，说明基于logistic 回归的分类预测模型可以更有效地预测企业的生存状况。

据此，提出以下政策建议：①中小企业的发展速度逐渐缓慢，效益逐渐降低，亏损、破产逐渐增多，相关部门和中小企业应积极合作，构建政府、金融机构和中小企业的合作平台，积极推行创新金融模式,可以极大地推动中小企业的发展和技术进步。②注册资本更低，企业生存时间更短，政府应采取积极的税收政策和货币政策支持其度过难关，解决中小企业融资难的问题，提高中小企业生命周期，降低中小企业死亡率。③民营企业对当地财税收入有很大的贡献，却比国有企业生存时间更短，地方政府应积极制定更多优惠政策，发展民营企业，实现民营企业与国有企业共同健康发展。