非线性区间型退化模型分析

管 强，刘桂红，林婷婷

（1．三明学院 信息工程学院， 福建 三明，365004；2 三明学院 人事处， 福建 三明，365004）

按照一定的设计要求和工艺方案所生产出来的合格产品，在规定的工作条件下均具有某种规定的功能，在可靠性理论中，将产品丧失所规定功能的现象称为失效[1]。针对退化型失效产品使用到一定的时间，都会慢慢地降低其功能但不完全丧失[2]，传统理论研究将产品失效定义为其性能退化[3]至低于或高于一个临界值（退化失效水平），如灯泡等元器件电性能衰退[4]、机械元件磨损、轮胎磨损、药品效用降低，这种定义虽然简单合理，但实际上不能完全描述产品退化失效问题。如轮胎磨损，不能简单的规定轮胎磨损高于到一个指定值就失效，毕竟轮胎是否失效在一定程度上取决于使用者的心理承受力， 胆小的使用者认为轮胎磨损至D1值就失效， 而胆大的使用者认为轮胎磨损至D2值才失效，一般的使用者则认为轮胎磨损至[D1，D2]中的一个值时失效。此时规定当轮胎的磨损达到在区间[D1，D2]中的一个值时认为轮胎失效就比较合理。针对单点型退化，近几十年来已有大量文献和学者对退化数据[5]提出了许多统计分析方法并取得了丰硕的研究成果。管强，汤银才[6]在传统单点退化的思想上提出区间退化模型， 并讨论了退化轨道是线性时的区间退化模型问题。本文则主要讨论退化轨道是非线性时的区间退化模型问题， 并利用数值积分[7]分析区间退化模型的寿命分布，将区间退化模型与传统单点模型进行对比，最后通过实例分析体现区间退化的合理有效性。

1 退化数据统计模型

1.1 退化轨道函数

假设一个产品的退化量不仅是时间的单调函数，而且依赖于一些参数α 与β，这样的函数称为退化轨道函数[7]，记为

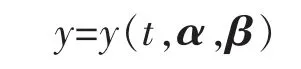
其中参数可分为两类：一类是固定参数（向量）α，它对总体中所有产品都是不变的；另一类是随机参数（向量）β，它随着产品不同而随机变化，一般假定β 服从某一分布fβ（θ），θ 是分布中的参数（向量）。

1.2 区间型退化失效分布函数

传统的失效标准是当产品的性能退化量超过或少于一个确定单点值时，即产品失效。然而这种单点型失效标准在现实应用中有时未必妥当，在这里对单点型失效标准进行修改，提出区间型退化失效标准，即当产品的性能退化量超过或少于一个区间型随机变量时产品失效。若产品寿命为T，退化量y（t，α，β）是增函数时，事件“产品在t 时刻之前失效”等价于“其退化量y（t，α，β）在t 时刻之前就达到失效区间水平D”，即“T≤t”等价于“y（t，α，β）≥D”。类似的，退化量y（t）是减函数时，“T≥t”等价于“y（t，α，β）≤D”，故产品寿命的分布函数为

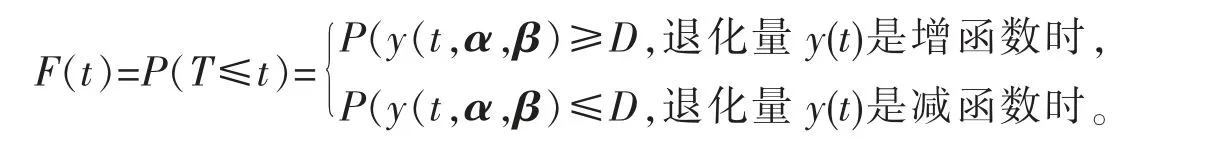
其中α 是确定参数（向量），β 是随机参数（向量），D 是介于区间[D1,D2]的随机变量。产品寿命的分布依赖于β 的分布和D 的分布，即依赖于轨道参数β，与失效区间水平D。

2 非线性-区间型退化模型寿命分布函数

2.1 两个参数的区间退化模型

设某产品的实际退化轨道是时间t 的非线性增函数，即

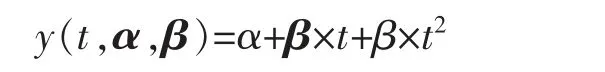
其中α 是固定参数，表示所有的试验产品在时刻0 时的初始退化量，而β 是随机参数，它是由产品间的差异引起的，表示退化率[9]。

考虑1 中β 与失效区间水平D 在不同情况下的寿命分布函数

定理1：设某产品的实际退化轨道是时间t 的非线性增函数，即

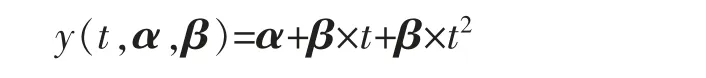
其中α 是固定参数，β 是随机参数，D 是失效区间水平，当β 服从正态N（μ，σ2），D 服从均匀分布U[D1,D2]时，T 寿命分布函数为

证明：

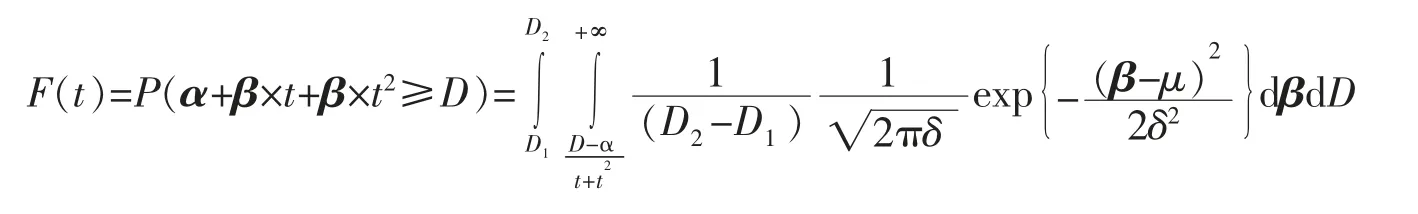
定理2设某产品的实际退化轨道是时间t 的非线性增函数，即

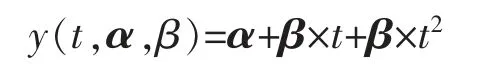
其中α 是固定参数，β 是随机参数，D 是失效区间水平，当β 服从对数正态分布LN（μ，σ2），D 服从U[D1,D2]时，T 寿命分布函数为

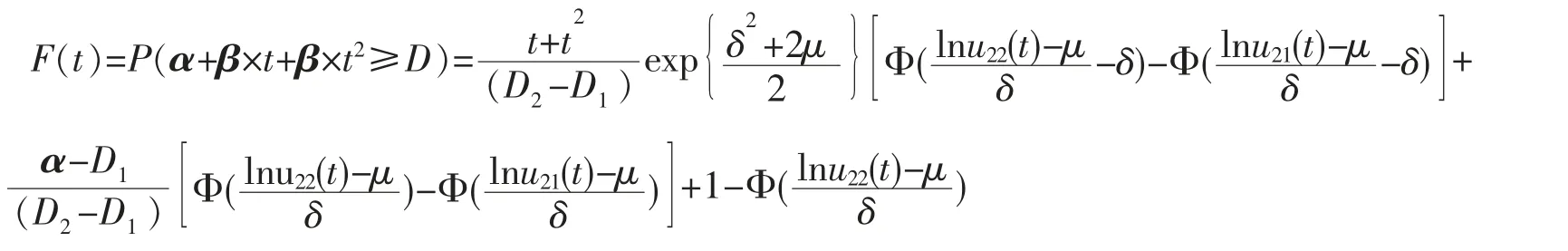
证明：

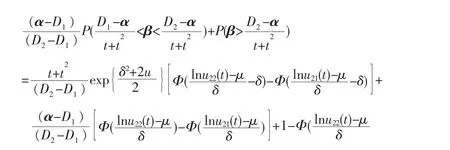
定理3设某产品的实际退化轨道是时间t 的非线性增函数，即

其中α 是固定参数；β 是随机参数；D 是失效区间水平。当β 服从威布尔分布Wei（m，η），D 服从U[D1,D2]时，T 寿命分布函数为

证明：

定理4设某产品的实际退化轨道是时间t 的非线性增函数，即

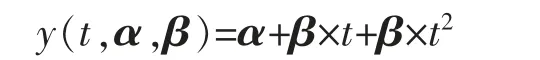
其中α 是固定参数，β 是随机参数，D 是失效区间水平，当β 服从伽马分布Γ（a，b），D 服从U[D1,D2]时，T 寿命分布函数为

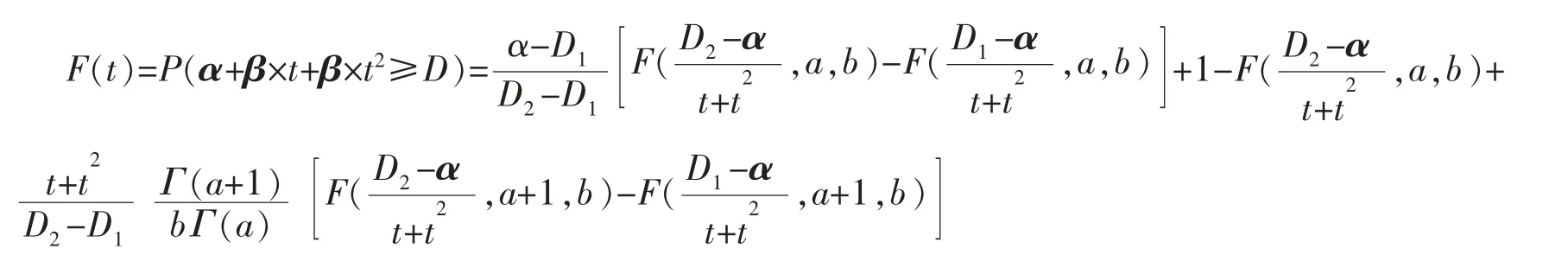
证明：

定理5设某产品的实际退化轨道是时间t 的非线性增函数，即

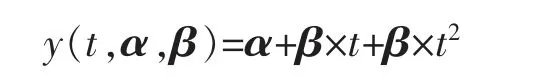
其中α 是固定参数，β 是随机参数，D 是失效区间水平，当β 服从均匀分布U（β1，β2），D 服从U[D1,D2]时，T 寿命分布函数为

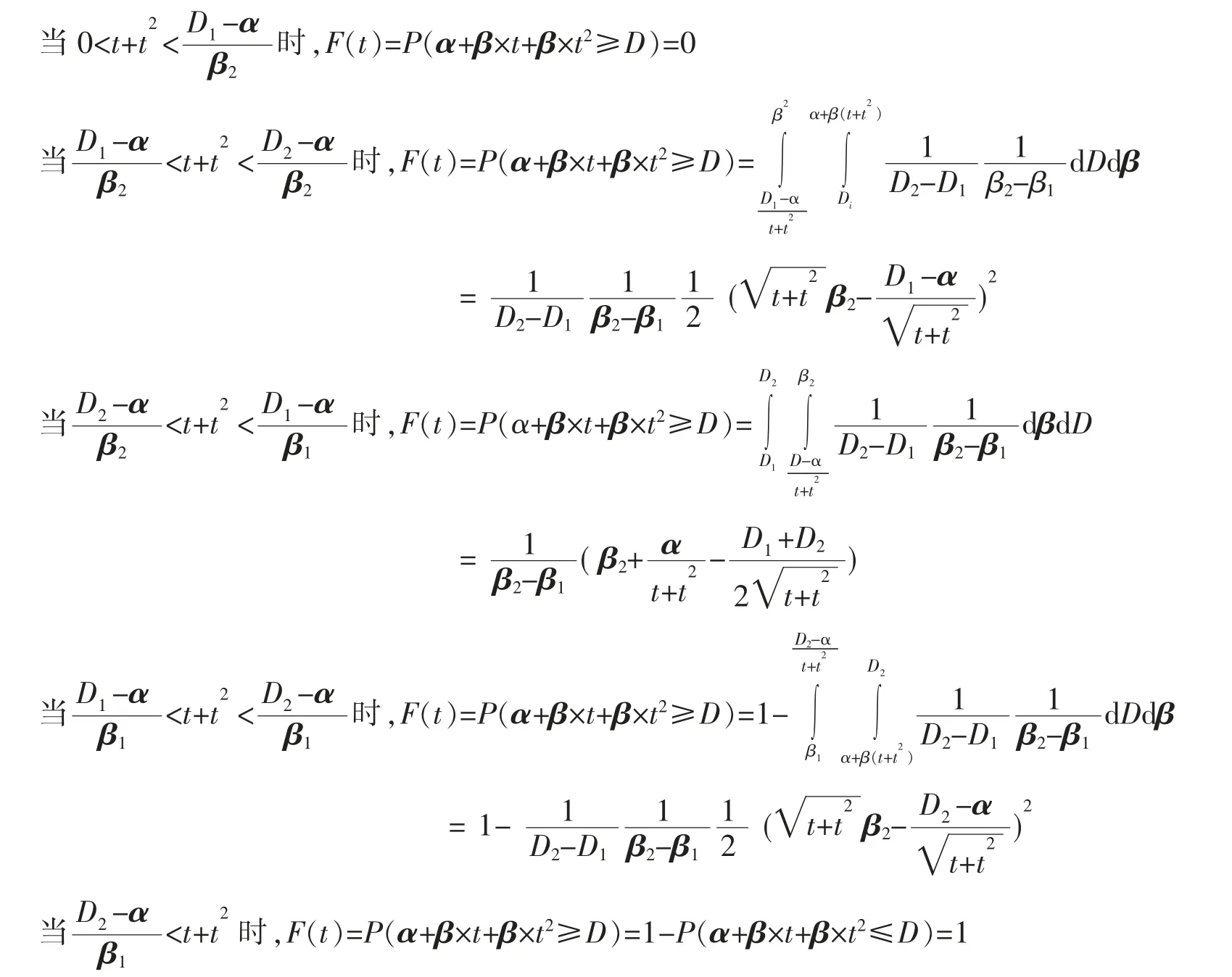
定理6设某产品的实际退化轨道是时间t 的非线性增函数，即

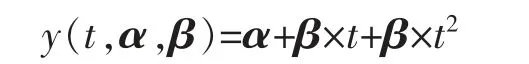
其中α 是固定参数，β 是随机参数，D 是失效区间水平， 当β 服从指数分布EXP （λ1），D 服从[D1,D2]时，截断指数分布EXP（λ2），T 寿命分布函数为

证明：

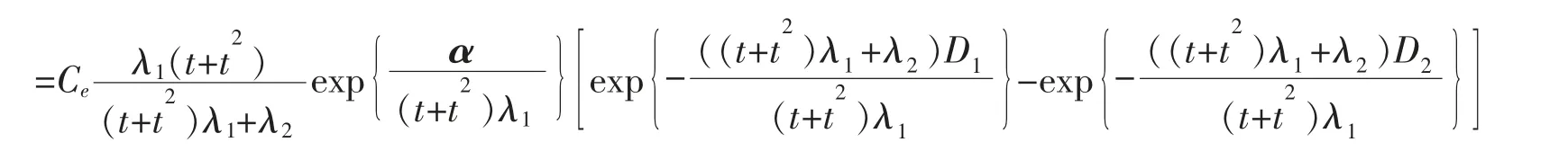
定理7设某产品的实际退化轨道是时间t 的非线性增函数，即

其中α 是固定参数，β 是随机参数，D 是失效区间水平，当β 服从正态分布N（μ1，δ21），D 服从[D1,D2]时，截断指数分布N（μ2，δ22），T 寿命分布函数为

证明：

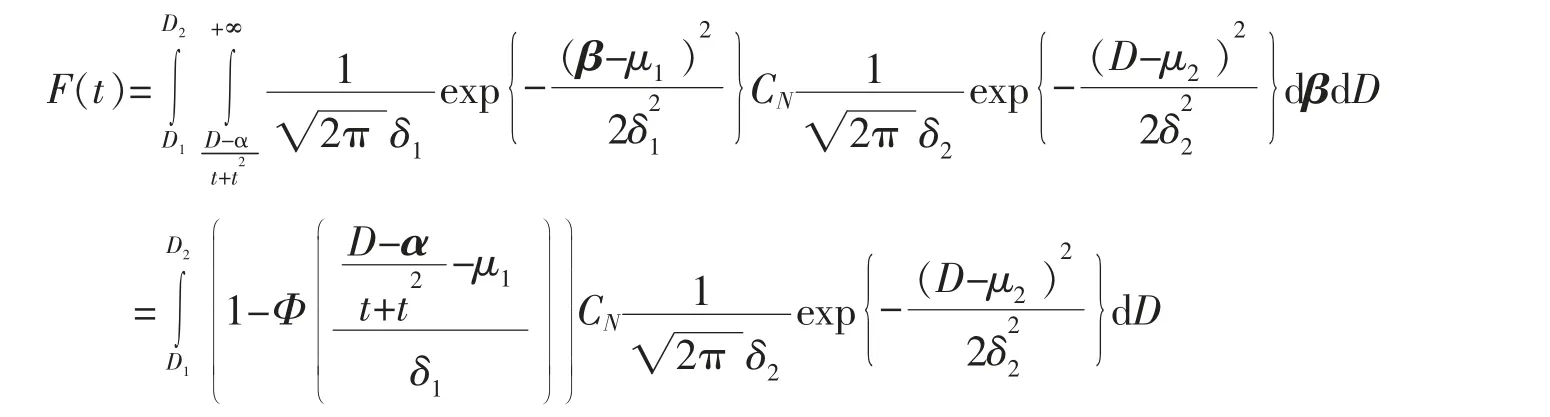
定理8设某产品的实际退化轨道是时间t 的非线性增函数，即

其中α 是固定参数，β 是随机参数，D 是失效区间水平，当β 服从对数正态分布LN（μ1，δ21），D 服从[D1,D2]时，截断指数分布N（μ2，δ22），T 寿命分布函数为

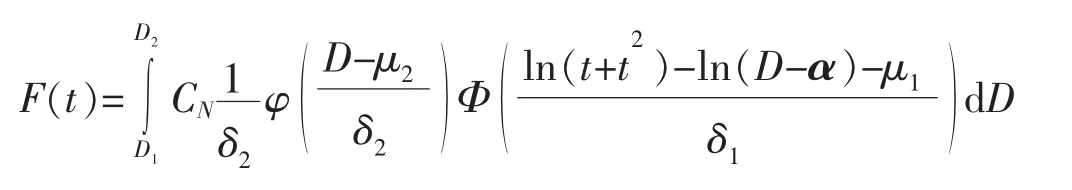
证明：

定理9设某产品的实际退化轨道是时间t 的非线性增函数，即

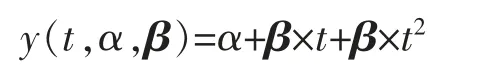
其中α 是固定参数，β 是随机参数，D 是失效区间水平，当β 服从威布尔分布Wei（m，η），D 服从[D1,D2]时，截断正态分布N（μ2，δ22），T 寿命分布函数为

证明：

定理10设某产品的实际退化轨道是时间t 的非线性增函数，即

其中α 是固定参数，β 是随机参数，D 是失效区间水平，当β 服从伽马分布Γ（a，λ），D 服从[D1,D2]时，截断正态分布N（μ2，δ22），T 寿命分布函数为

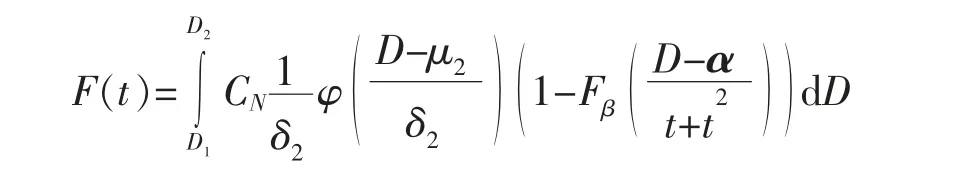
证明：

其中Fβ（x）是伽马分布Γ（a，λ）的分布函数.

定理11设某产品的实际退化轨道是时间t 的非线性增函数，即

其中α 是固定参数，β 是随机参数，D 是失效区间水平， 当β 服从对数正态分布LN （μ1，δ21），D 服从[D1,D2]时，截断正态分布N（μ2，δ22），T 寿命分布函数为

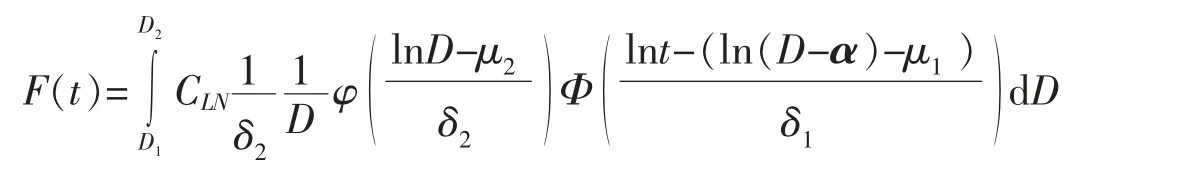
证明：

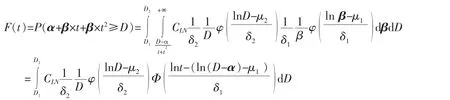
上面对常见11 种非线性区间退化模型进行了讨论，获得了其对应寿命分布，其中部分寿命分布函数没有显示表达式，其求解可以采用数值积分和蒙特卡罗积分求解。寿命分布求出后，就可以对产品寿命各种特征进行推断。

2.2 三个参数的区间退化模型

设某产品的实际退化轨道是时间的非线性增函数，即

其中α 是固定参数，表示所有的试验产品在时刻0 时的初始退化量，而β1是β2随机参数，它是由产品间的差异[10]引起的，表示退化率。

定理12设某产品的实际退化轨道是时间t 的非线性增函数，即

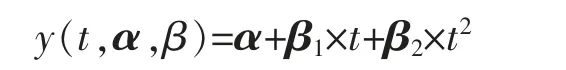
其中α 是固定参数，当β1服从正态N（μ1，σ21），β2服从正态N（μ1，σ22），D 服从U[D1,D2]时，T 寿命分布函数为

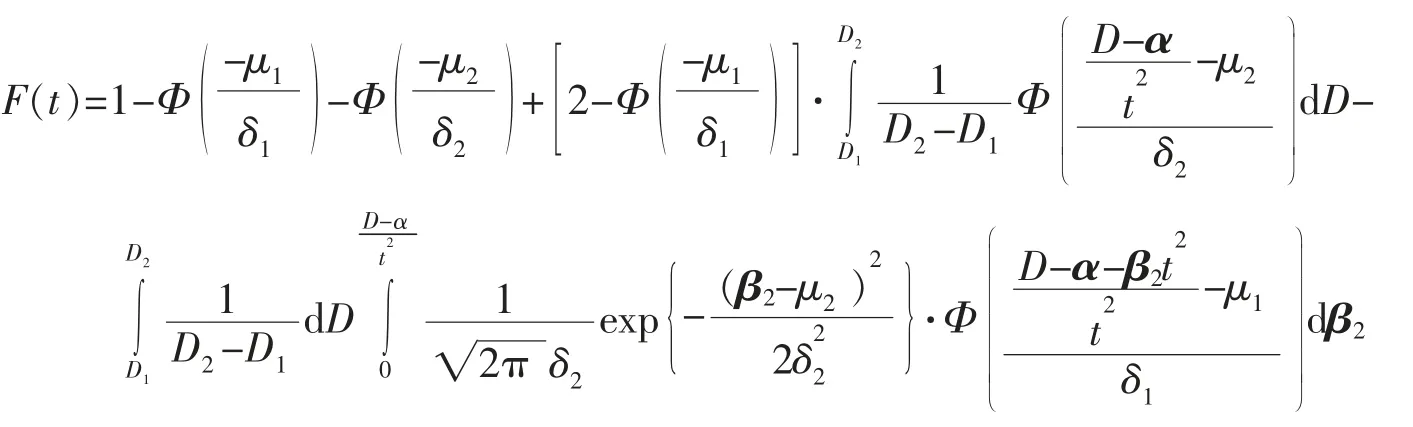
证明：

定理13设某产品的实际退化轨道是时间t 的非线性增函数，即

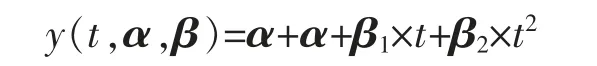
其中α 是固定参数，β 是随机参数，D 是失效区间水平，β1服从正态N （μ1，σ21），β2服从对数正态LN（μ1，σ22）D 服从U[D1,D2]时，T 寿命分布函数为

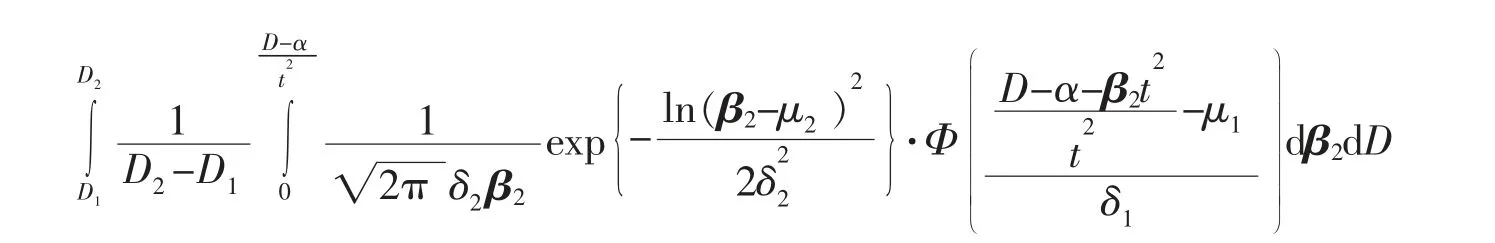
证明：

3 区间型退化模型寿命分布函数数值解

对于第2 节所求没有显示表达式的寿命分布函数[11]，可以采用蒙特卡罗积分[12]进行。从第2 节第7～11 种情况发现这些没有显示表达式的寿命分布函数都具有如下形式积分

其中f（x）是服从区间U[D1,D2]上已知确实的某一个分布的密度函数，g（t，x）是已知确定的某一个二元函数。因此F（t）可以按如下步骤计算

1.对给定的t，从服从的分布汇总抽取N 个样本(x1,x2，…，xN）

对于一般退化轨道2.1，和区间失效水平D，其寿命分布函数的蒙特卡罗解按如下步骤进行：

1.根据退化数据，采用极大似然估计等方法估计出β 分布中参数的估计以及固定参数α 的估计；

2.由β的分布fβ（）分中产生一个样本，把它带入退化轨道同时区间失效水平D从区间[D1,D2]中按事先给定分布随机产生一个失效水平，然后按计算首次达到的时间；

3.步骤2 重复N 次，譬如N=1 000 000，可得N 个首次达到的时间；

4 模拟例子

4.1 精确解例子

为了对比单点型退化与区间型退化寿命分布的关系，假定单点型中固定退化水平值是区间型退化水平区间中间值，如单点型失效水平取值为40，则区间型失效水平取[38,42]，[36,44]等，否则两者不好对比，失去对比意义。下面我们根据第3 节给出的区间-非线性退化分布函数，分别画出单点型和区间型分布函数图。

1）假设第2 节第1 种情况（正态分布-均匀分布）线性模型中α=1，β～N（0.5，0.052）区间型退化D 服从均匀分布[38,42]和[36,44],单点型退化D=40。进行模拟求解得单点型退化和区间型退化分布函数图（见图1）。

从图1中可以看出区间退化失效分布与传统单点型退化分布函数是有区别的，且在前半部分时间里区间失效分布函数值大于传统单点型退化分布函数值，后半部分时间里则相反。随着均匀分布区间接近于单点时，其分布函数趋于单点型退化分布函数。

2）假设第2 节第2 种情况（对数正态分布-均匀分布）线性模型中α=1，β～LN（0.5，0.052），区间型退化D 服从均匀分布[38,42][36,44],单点型退化D=40。求得它们分布函数图（见图2）。从图2中，可以看出区间退化失效分布与传统单点型退化分布函数有显著区别，其他规律类似（正态分布-均匀分布）情况。

图1 轨道正态分布-失效水平均匀分布线性模型下的分布函数

图2 轨道对数正态分布-失效水平均匀分布线性模型下的分布函数

3） 假设第2 节第3 种情况 （威布尔分布-均匀分布） 线性模型中α=2，β 服从威布尔分布Wei（2,2），类似求得它们分布函数图（见图3）。从图3中，可以看出区间退化失效分布与传统单点型退化分布函数区别不明显。

4）假设第3 节第4 种情况（威布尔分布-均匀分布）线性模型中α=1，β 服从伽马分布Γ（6,12），类似求得它们分布函数图（见图4）。从图4中，可以看出区间退化失效分布与传统单点型退化分布函数区别不明显。

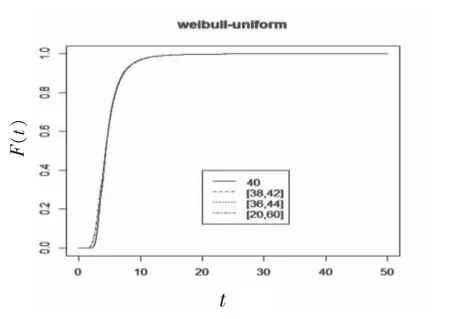
图3 轨道威布尔分布—失效水平均匀分布线性模型下分布函数

图4 轨道伽马分布—失效水平均匀分布线性模型下分布函数

5)假设第2 节第5 种情况（均匀分布-均匀分布）线性模型中α=1，β 服从均匀分布U[0.3，0.6)，类似求得它们分布函数图（见图5）。从图5中，可以看出区间退化失效分布与传统单点型退化分布函数区别明显，其它规律类似（正态分布-均匀分布）情况。

6）假设第2 节第6 种情况（指数分布-指数分布）线性模型中α=1，β 服从指数分布EXP（2），失效水平D 服从截断指数分布EXP（2），类似求得它们分布函数图（见图6）。从图6中，可以看出区间退化失效分布与传统单点型退化分布函数区别明显，其它规律类似（正态分布-均匀D 分布）情况。

图5 轨道均匀分布-失效水平均匀分布线性模型下的分布函数

图6 轨道指数分布-失效水平截断指数分布线性模型下的分布函数

4.2 数值解例子

下面给出第2 节中寿命分布函数没有显示表达式时的模拟情况

1）假设第2 节第7 种情况（正态分布-正态分布）线性模型中α=1，β～N（0.5,0.52）服从区间上截断正态分布N（40,52）。求出寿命分布数值积分（见图7）。从图7中，可以看出区间退化失效分布与传统单点型退化分布函数区别明显，其他规律类似（正态分布-均匀分布）情况。

2）假设第2 节第8 种情况（对数正态分布-正态分布）线性模型中α=1，β～LN（0.8,0.052）失效水平D 服从区间上截断正态分布N（40,52）。求出寿命分布数值积分（见图8）。从图8中，可以看出区间退化失效分布与传统单点型退化分布函数区别明显。

3）假设第2 节第9 种情况（威布尔分布-正态分布）线性模型中α=1，β 服从威布尔分布Wei（0.6,4），失效水平D 区间上截断正态分布N（40,52）。利用蒙特卡罗积分求得其寿命分布（见图9）。从图9中，可以看出区间退化失效分布与传统单点型退化分布函数区别不明显。

4） 假设第2 节第10 种情况 （伽马分布-正态分布） 线性模型中α=1，β 服从伽马分布Γ（4,0.5），失效水平D 服从区间上截断正态分布N（40,52）。利用蒙特卡罗积分求得寿命分布数值积分（见图10）。从图10 中，可以看出区间退化失效分布与传统单点型退化分布函数区别不明显。

5）假设第2 节第11 种情况（对数正态分布-对数正态分布） 线性模型中α=1，β服从对数正态分布LN（0.8,0.052），失效水平D 服从区间上截断对数正态分布LN（3.7,1.32）。利用蒙特卡罗积分求得寿命分布数值积分（见图11）。从图11 中，可以看出区间退化失效分布与传统单点型退化分布函数区别明显。

图7 轨道正态分布-失效水平截断正态分布线性模型下的分布函数

图8 轨道对数正态分布-失效水平截断正态分布线性模型下的分布函数

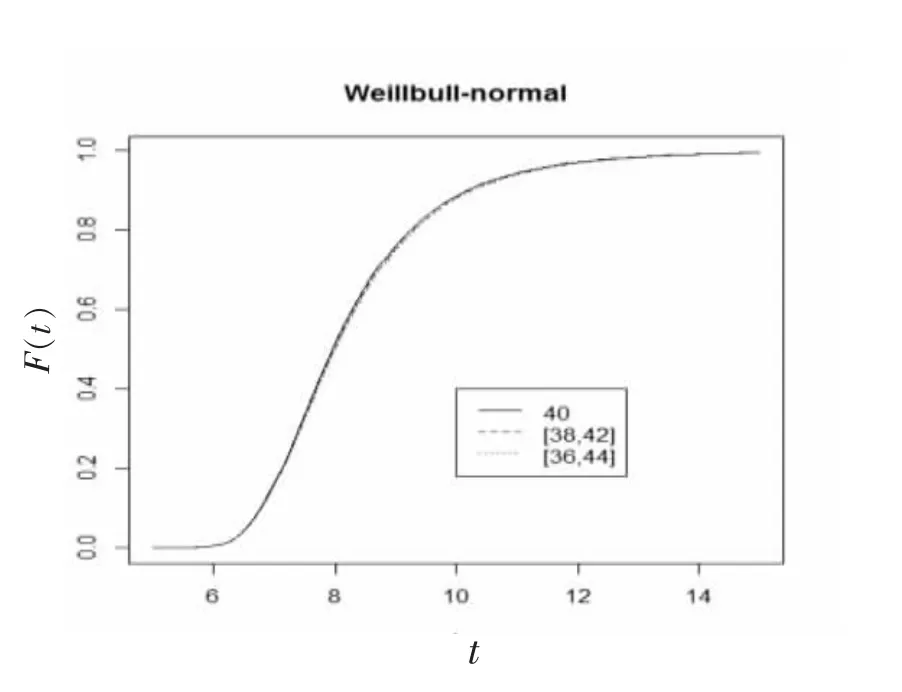
图9 轨道威布尔正态分布-失效水平截断正态分布线性模型下的分布函数

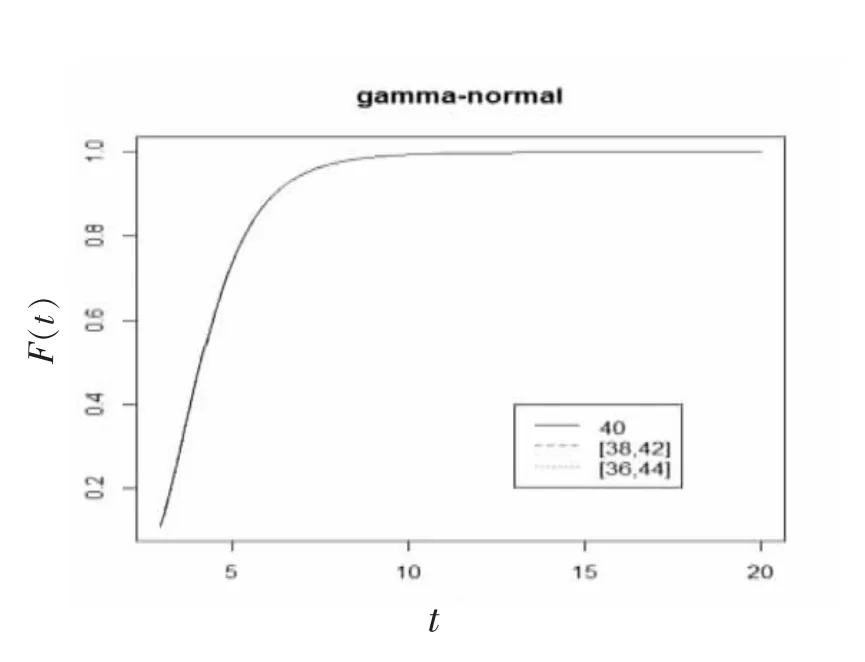
图10 轨道伽马分布-失效水平截断正态分布线性模型下的分布函数

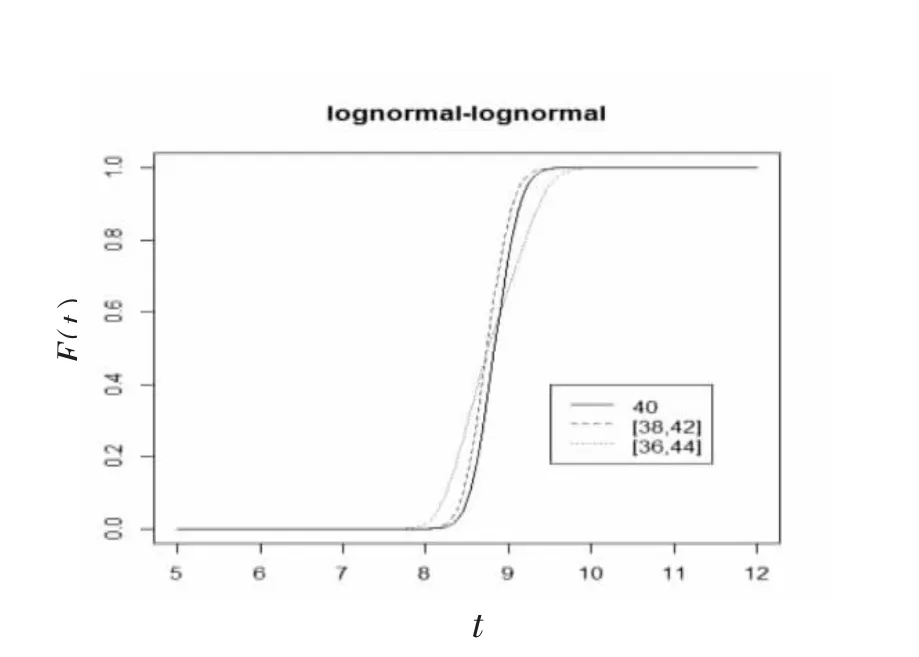
图11 轨道对数正态分布-失效水平截断对数正态分布线性模型下的分布函数

5 结果和展望

本文针对非线性退化轨道情况，详细讨论和求解出五种情况下区间退化寿命分布函数，并利用蒙特卡罗数值积分法给出区间退化寿命分布函数无显式时的求解步骤和方法。通过模拟分析对比了单点型退化和区间型退化寿命分布函数的关系。当区间缩小至单点时，区间型退化寿命分布就接近于单点型退化寿命分布函数；当区间对称离开单点时，区间型退化寿命分布与单点型退化寿命分布函数就有区别，其区别强度与退化轨道随机参数分布息息相关。从模拟5 中情况结果中发现当退化轨道随机参数服从对数正态分布时区间型退化寿命分布与单点型退化寿命分布函数区别最明显。因此在实际应用中，当失效机理不够确定时，使用传统单点型退化模型进行推断，就会产生较大误差。

虽然本文给出了区间型退化分析一般的解决思路，但是对于不同的退化轨道和失效水平分布其寿命分布求解是千差万别的，其单点型退化寿命分布与区间型退化寿命分布关系还需进行研究。传统单点型加速退化[13]，竞争退化[14]，退化优化设计[15]等方面也可以考虑推广至区间型加速退化[16]，竞争退化，退化优化设计等。因此未来区间型退化模型的研究还可以进一步深入。