饱和非线性约束离散时间时滞系统鲁棒H∞控制

王留海，肖民卿，冯青香

（1.福建师范大学 数学与信息学院，福建 福州350007；2.福建省分析数学及应用重点实验室，福建 福州350007）

饱和现象普遍存在生物、工程及社会经济等实际系统中，饱和约束是计算机控制、数字信号处理等领域中不可避免的问题，也是数字滤波器设计、神经网络控制等领域中的常见问题。

系统中非线性包括溢出和量化非线性，通常是导致系统不稳定性的因素。一般情况下，研究饱和非线性的影响时，主要考虑溢出非线性。另外，时滞现象也是普遍存在的，是造成系统不稳定和性能变差的主要根源。近年来，时滞系统的分析研究得到许多学者关注。文献[1]讨论了线性离散时变时滞系统的状态反馈控制问题。文献[2-3]讨论了饱和非线性不确定离散时间时滞系统，给出了使闭环系统渐近稳定的新判据。文献[4-5]讨论了线性离散时间不确定系统的鲁棒H∞控制问题，文献[6]讨论了一类非线性系统的鲁棒控制问题。文献[7-12]讨论了不确定系统的鲁棒H∞控制器设计问题，给出了相应的控制器设计方法，这些工作研究了给定扰动抑制水平γ 的H∞控制器的设计方法。文献[15-16]中, V.Krishna Rao Kandanvli, Haranath Kar 等人讨论了一类饱和不确定离散时间时滞系统的鲁棒渐近稳定性问题，通过引用对角占优矩阵为附加矩阵，给出状态饱和约束条件下系统渐近稳定的充分条件。到目前为止，对含有饱和非线性状态约束的时滞系统的研究已有较多成果，然而关于含有饱和非线性状态约束的离散时间时滞系统的鲁棒性能分析和控制器设计的研究却很少见到报道。

鉴于此，本文利用“严格超度量矩阵的逆为行对角占优矩阵”[13-14]这一结论，构造适当的Lyapunov-Krasovskii 函数，引入参数，给出了系统存在鲁棒H∞控制器的一个新的判别准则，进而基于该准则，设计了使得闭环系统渐近稳定且满足最优H∞性能的状态反馈控制器。最后，通过算例验证了该方法的有效性。

1 问题描述

考虑具有饱和非线性状态约束的离散时间时滞系统：

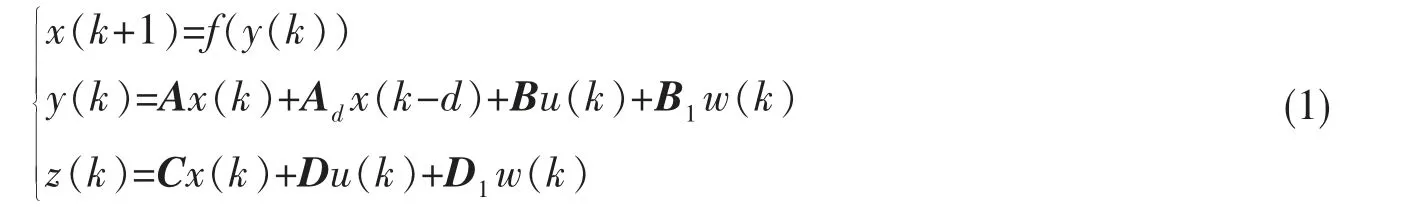
其中x（k）∈Rn是系统状态向量，u（k）∈Rm是控制输入，w（k）∈Rp是外部扰动输入，且是平方可和的，即w（k）∈L2[0，∞），z（k）∈Rq是被调输出，A，Ad，B，B1，C，D，D1是适当维数的实常数矩阵，d 是滞后时间。饱和非线性约束函数为:

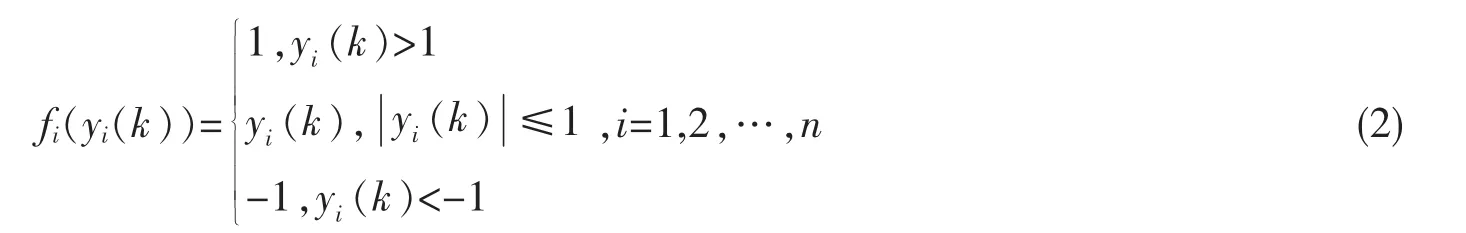
本文研究的问题是对给定的常数γ＞0，设计一个状态反馈控制律u（k）=Kx（k），使得闭环系统满足以下设计指标。

闭环系统是渐近稳定的；在零初始条件x（0）=0 下，对任意非零w（k）∈L2[0，∞），系统被调输出z（k）满足表示空间L2[0，∞）中的标准范数。

满足以上指标状态反馈控制律u（k）=Kx（k）称为系统(1)的γ-次优H∞控制律。另外，使得γ 最小化的控制律u（k）=Kx（k）称为系统(1)鲁棒H∞最优保性能控制律。

考虑状态反馈控制律u（k）=Kx（k）， 其中K 是待设计的定常反馈增益矩阵。将控制律应用到系统(1)，可以得到闭环系统

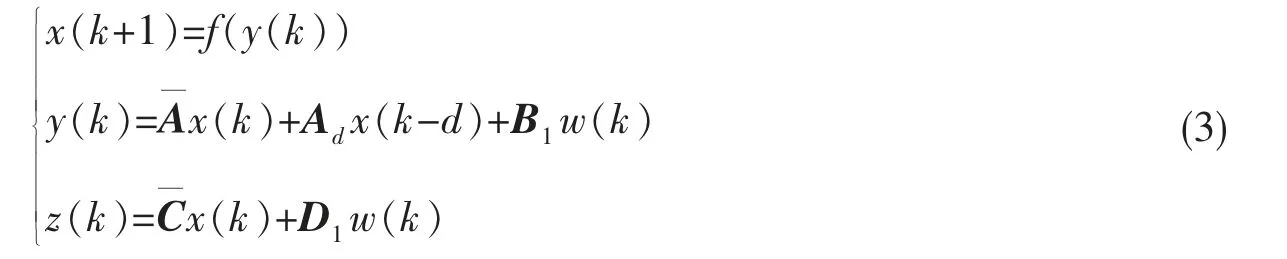
引理1[15]给定适当维数矩阵Ω1，Ω2，Ω3其中Ω1和Ω2是对称的，则Ω1-Ω3Ω2-1Ω3T＞0 和Ω2＞0，当且仅当

定义1[13]矩阵N=[aij]∈Rm×n是严格超度量矩阵，要满足下列条件：

引理2[13]如果矩阵N=[aij]∈Rn×n是一个严格超度量矩阵，那么N 是可逆非奇异矩阵，且它的逆矩阵是一个严格对角占优超度量矩阵，(即N-1=[bij]∈Rn×n是实对称正定矩阵， 当bij＞0，i≠j 和bii＞并有bij=0 当且仅当aij=0。

引理3[15]若G=[gij]是一个对称正定矩阵，且满足

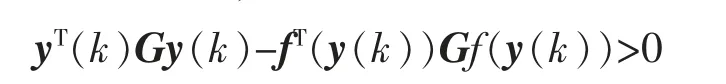
当且仅当G 是一个对角占优矩阵。

2 主要结论

定理1对给定常数γ＞0，闭环系统(3)存在γ-次优H∞控制律u（k）=Kx（k）的一个充分条件是存在对称矩阵P，S 和严格对角占优的矩阵G=[gij]，有：

证明：考虑Lyapunov 函数：

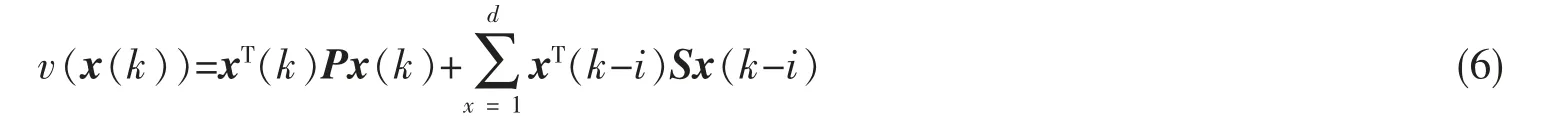
沿着闭环系统(3)的状态轨迹，v（x（k））的前向差分为

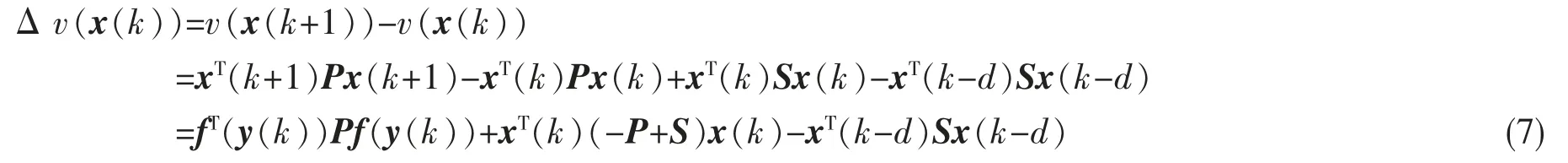
考虑给定的常量δ＞0，即

由(3), (7)和(8)式知，有

其中

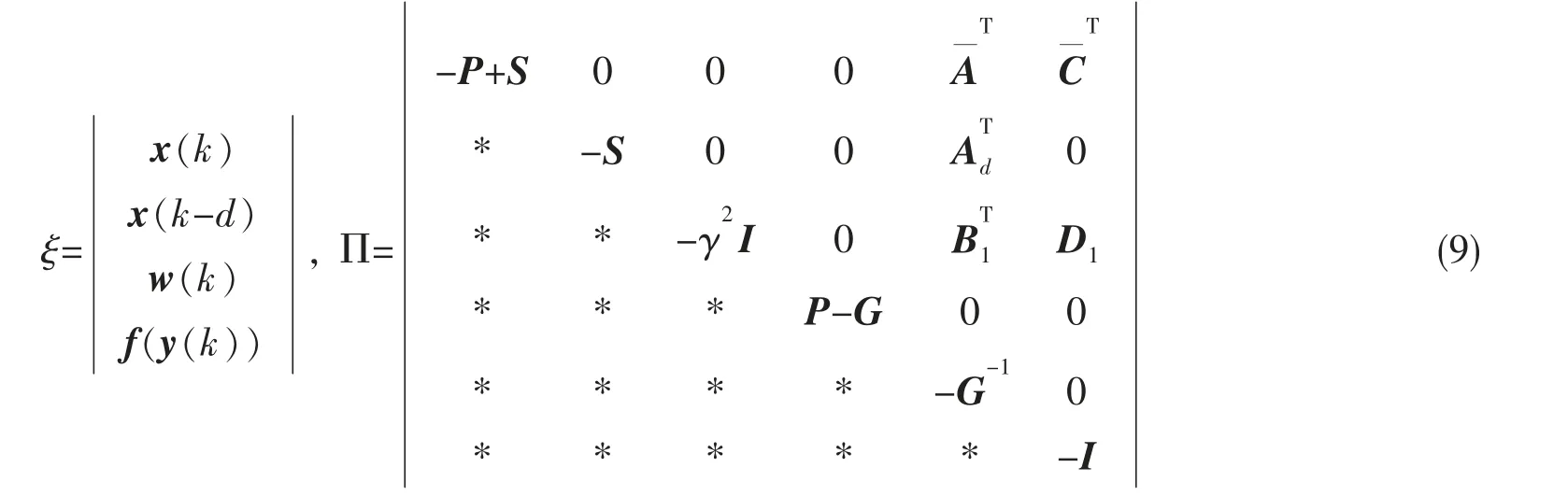
若Π＜0，可得Δ v（x（k））+δ+zT（k）z（k）-γ2wT（k）w（k）＜0。

由零初始条件，可得

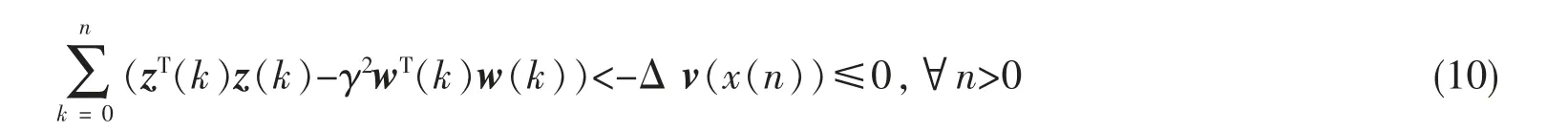
又有w（k）∈L2[0，∞），可得定理得证。

定理2对于给定常数γ＞0，如果存在对称正定矩阵X 和T、严格超度量矩阵N 和适当维数的矩阵Y，满足矩阵不等式（11）。

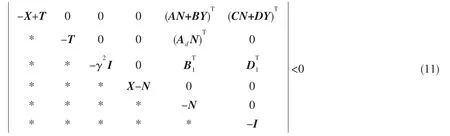
则u（k）=YN-1x（k）是系统（3）的一个γ-次优H∞控制律。

证明：由矩阵不等式(5)可写成去

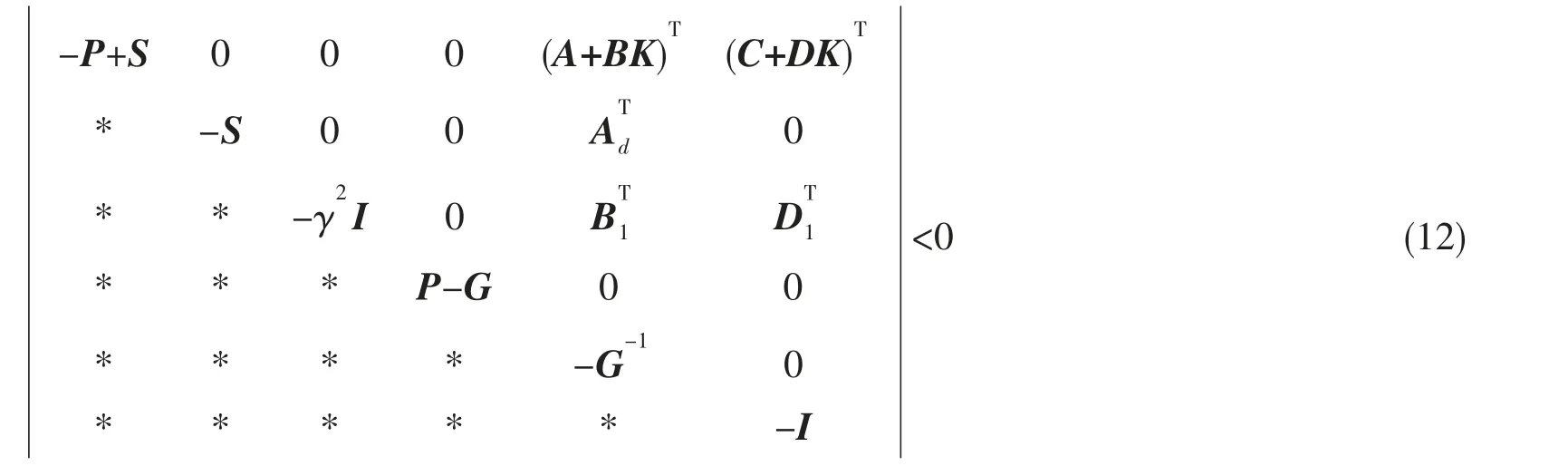
用矩阵diag{G-T，G-T，I，G-T，I，I}分别左乘和右乘(12)，并记X=G-TPG-1，T=G-TSG-1，N=G-1，Y=KG-1，即可得矩阵不等式(11)。定理得证。

另外，基于γ-次优控制器H∞的存在条件(5)，通过变量替换γ2=ρ，建立和求解以下优化问题

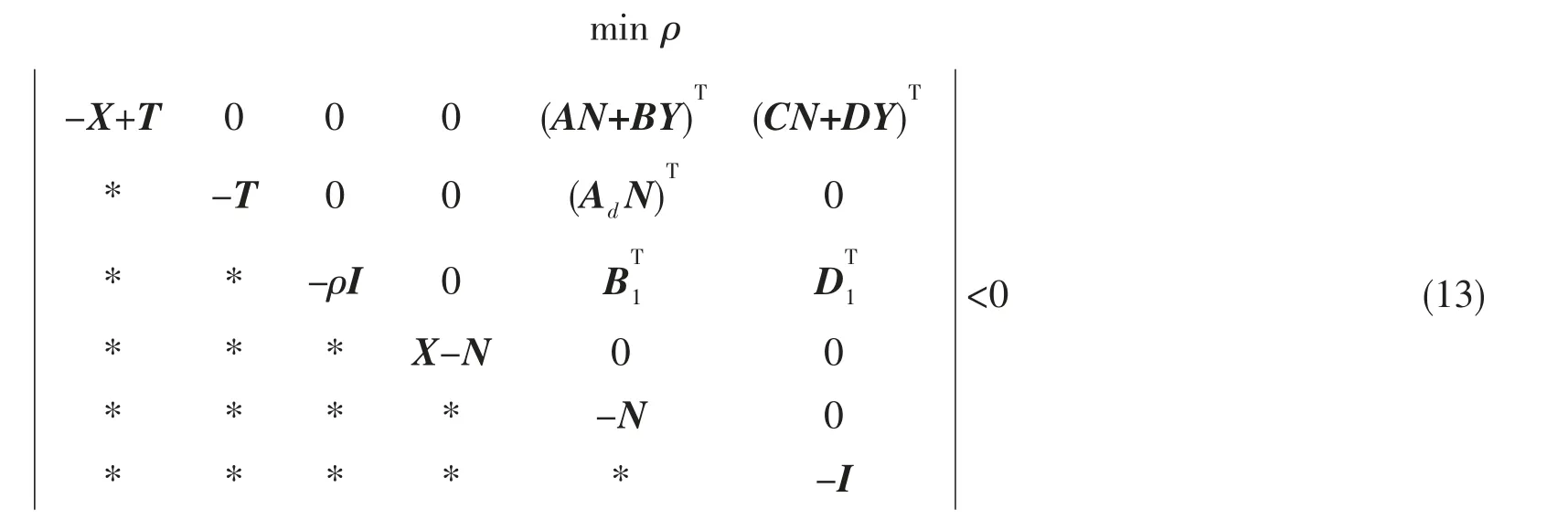
这就给出了系统(3)的最优鲁棒H∞状态反馈控制律的设计方法。很容易看到不等式(13)是一个具有LMI 约束和线性目标函数的凸优化问题， 因此利用LMI 工具箱中的求解器求解该问题的全局最优解。从而设计出最小化的性能指标的状态H∞状态反馈控制器。

3 算例

考虑具有饱和非线性约束的离散时滞系统(1)，其中

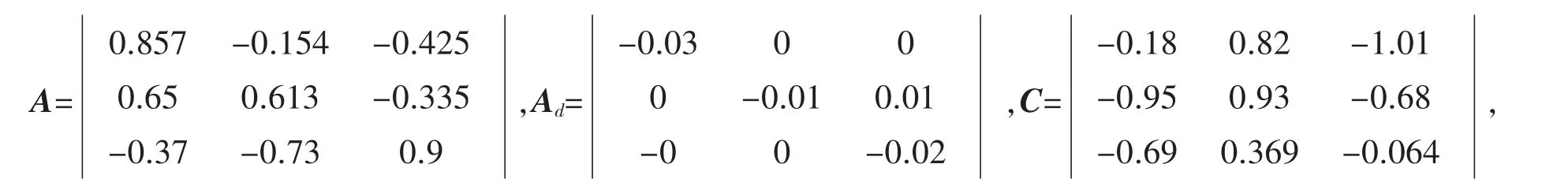
D=[-0.7 0.5 0.2]T，D1=[0.5 0.2 0.1]T，B=[0.2 -0.4 0.68]T，B1=[0.1 -0.6 0.3]T，d2=2 系统初始状态x（-2）=[1 1 1]，x（-1）=[2 1.2 0.8]，x（0）=[-1.3 0.8 -2]，扰动方程为w（t）=0.5cos（2πk）exp（-k）。由于A 的特征值为1.5586,0.4057+0.3426i,0.4057-0.3426i，所以矩阵A 是不稳定的。初始系统H∞状态轨线如图1所示。现在考虑该系统H∞状态反馈控制器问题。通过应用LMI 工具箱中的求解器mincx 来求解相应的优化问题(13)，可得该问题的最优解是：

通过可行解易构造出该系统γ 最小化H∞的状态反馈控制律

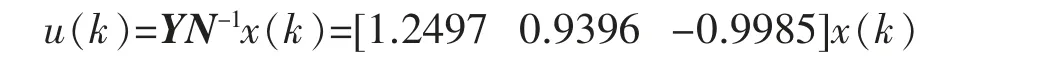
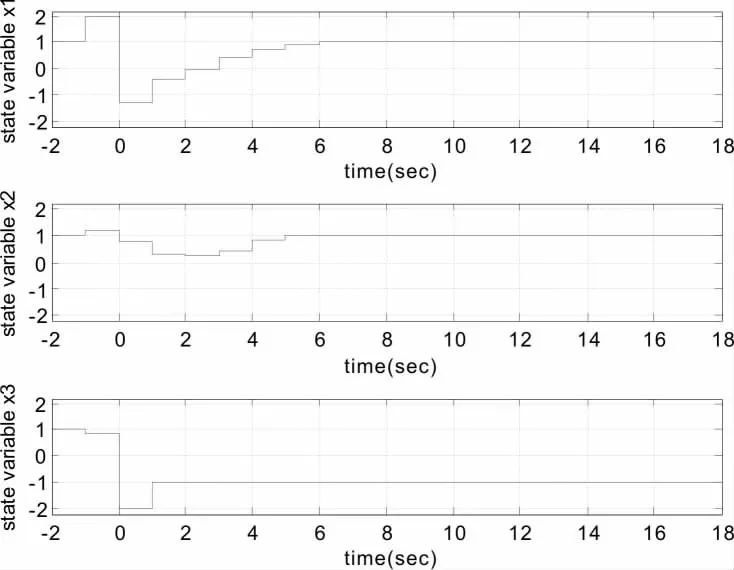
图1 初始系统的状态轨线

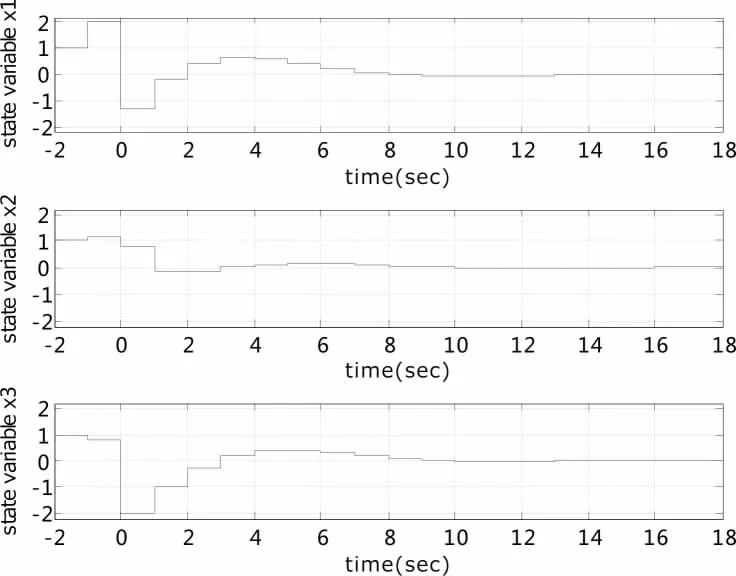
图2 闭环系统（3）的状态轨线

4 结论

本文研究了一类带有饱和非线性约束的离散时间时滞系统的鲁棒H∞控制问题， 通过采用LMI的处理方法， 导出了一组LMI 的可行性表示该闭环系统的γ-次优H∞状态反馈控制律存在的充分条件，进而通过变量替换求解一个凸优化问题，给出了满足控制约束的最优状态H∞控制律的设计方法。最后，通过算例验证了该方法的有效性。