一种新的脉冲联合调制水声通信方法

张路蔚，刘凇佐，王嘉玮，陶剑锋

(1.杭州应用声学研究所，浙江 杭州 310012；2.哈尔滨工程大学，黑龙江 哈尔滨 150001)

0 引 言

混沌是一种非线性的类伪随机的表现形式，易于产生、易于再生、确定性、类随机、非相关和种类众多是该系统的特点[1]。混沌序列是一种非周期码序列，具有码元库数量大、不同映射对应的混沌序列以及不同相位对应的混沌序列永远不重复的特点，混沌序列的统计特性可近似看作高斯白噪声[2]。将混沌序列应用在编码通信与调制通信中可以获得较强的抗截获性和保密性，因此，混沌通信将成为隐蔽水声通信中的一个重要发展方向[3]。经典的时间离散混沌映射系统包括逻辑斯蒂克(Logisic)映射、契比雪夫(Chebyshev)映射和帐篷(Tent)映射[4]。Patten时延差编码(Pattern Time Delay Shift Coding,PDS)在通信中为脉位编码，将信息调制到码元的时延信息中，不同的时延值代表不同的信息，具有较强的抗多普勒和抗多途扩展能力，但PDS采用的码元长度是固定的，这会导致通信速率的下降以及时间压缩扩展时解码带来的高误码率。混沌脉宽调制(Chaotic Pulse-Width Modulation,CPWM)和混沌脉位调制(Chaotic Pulse-Position Modulation,CPPM)是基于PSD体制提出的新技术，目前研究人员已经在水声通信应用中对这两种技术做出了探索性的研究[5]。CPPM技术最大的特点是其在非相干解调时不需要每一帧都加入同步头，而是具有自同步特性。之后相继提出了混沌脉冲宽度调制(CPWM)技术。不论是CPPM技术或是CPWM技术，每个完整混沌脉冲都只携带1 bit信息。本文研究了联合CPPM与CPWM技术，提出一种混沌脉位、脉宽联合调制的通信方法，将信息分别调制到混沌脉冲信号的脉位与脉宽上，使得一个完整脉冲携带2 bit信息，通信速率最高可提高到2倍，有效通信带宽增加，通信隐蔽性增强。文章讨论了混沌脉位-脉宽联合调制(Chaotic Pulse-Position and Pulse-Width Joint Modulation,CPPPWM)系统参数选取问题，通过仿真实验对CPPPWM系统的误码率性能进行分析，并分析验证了CPPPWM系统的有效性。

1 新型混沌脉位-脉宽调制通信系统

CPPPWM是结合了脉宽调制与脉位调制技术，使用混沌编码对脉冲的脉宽与脉位长度进行调制的一种联合调制通信方式。CPPPWM将二进制信息分别调制到混沌调制的脉宽与脉位上，即每一个完整脉冲可承载2 bit信息。图1是CPPPWM调制解调的原理图[6]。

图1中的混沌脉冲生成器的核心是比较器。计数器在混沌脉冲生成器运行时处于自由运行模式，在此模式下产生一个线性增长的信号C(t)=K1t，其中K1是线性增长信号的增长斜率，又叫做计数步长。每当脉冲到达时，C(t)进行零重置。在重置时刻tn之前，计数器输出值暂时寄存，同时将输出值送入非线性转换器F(⋅)中。用一个放大器来产生另一个线性增长的信号A(t)=KK1t=K2t，K是放大器增益，且K＞1(即K2＞K1)，所以信号A(t)的增长斜率大于信号C(t)的增长斜率。当放大器输出信号的能量级等于计数器输出信号的能量级F()时，输出1与输出2先后输出两个窄脉冲，输出时间分别为输出2的脉冲产生时间要比输出1的脉冲产生时间早，且脉冲产生时间受控于增益K和计数步长K1的值。输出1与输入端连接形成一个闭路环，根据脉宽与脉冲周期适当调节参数，混沌脉冲生成器的两个输出端将产生两组混沌脉冲序列，相邻脉位按F(⋅)规则变化。

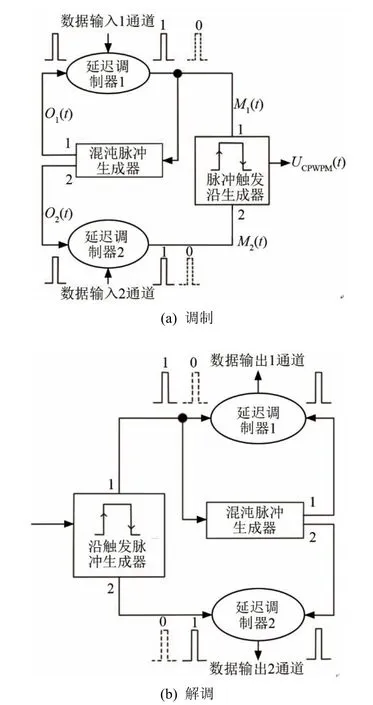
图1 CPPPWM调制与解调原理图Fig.1 Schematic diagrams of CPPPWM and its demodulation

1.1 CPPPWM调制

在CPPPWM调制模块中，混沌脉冲生成器反馈回路输出的二进制信息O1(t)和O2(t)分别在延迟器1和延迟器2的作用下被调制到两个连续脉冲的脉冲间隔上。输入端的脉冲触发数据源在延迟调制器处可以得到下一组二进制信息和。根据二进制信息的值，输入脉冲O1(t)和O2(t)被延迟的时间为和。其中，d1和d2是时间延迟常数项，可保持系统同步性；m1和m2是调制幅度，反映了“0”比特与“1”比特之间的延迟时间差。因此，延迟调制器输出的延迟脉冲M1(t)和M2(t)产生时间分别为产生混沌脉冲序列将作用到脉冲触发沿生成器上，随着M1(t)和M2(t)的触发，脉冲触发沿生成器的输出会转换到相应的高低电平，以此定义混沌调制的脉位和脉宽[4]。脉冲触发沿生成器输出的脉冲序列即为CPPPWM信号，数学表达式为

其中，u(t)是单位阶跃函数，tn是产生第n个脉冲的时刻，A是脉冲幅度，Δτn是脉冲宽度。第n条脉冲宽度与第n+1条脉冲位置的定义为

CPPPWM联合调制下的脉冲间隔与脉宽Δτn都承载了二进制信息，且ΔTn与Δτn的变化取决于混沌映射F(⋅)。

CPPPWM调制方法下，脉宽Δτ与脉位ΔT都被用来调制二进制信息，且使用非线性函数F(⋅)来控制Δτ与ΔT的变化。由式(2)可知，CPPPWM下的Δτ与ΔT取决于参数m1、m2，d1、d2，K1、K2和F(⋅)，所以CPPPWM调制方法下的脉宽脉位以混沌的方式变化。CPPPWM调制方式图解如图2所示。

图2 CPPPWM，PPM，PWM调制位置图Fig.2 Modulation position diagram of CPPPWM,PPM and PWM

1.2 CPPPWM解调

CPPPWM解调最直观的方法就是调制的逆过程。如图1(b)所示，接收信号需要送入脉冲触发沿生成器中。脉冲触发沿生成器通过上升沿或下降沿触发，在其输出1和输出2的端口产生窄脉冲。脉冲触发沿生成器的输出1与混沌脉冲生成器相连，连接方式与调制模块完全相同。理论上，由于系统保持同步状态，所以混沌脉冲生成器输出端重新生成的混沌脉冲序列与送入调制端口的完全相同。混沌脉冲生成器的输出脉冲送入延迟调制器1和2，与相应的脉冲触发沿生成器的输出脉冲作对比，进而得到延迟时间Δτn-F(Cn)/K2和ΔTn+1-F(Cn)/K1。二进制信息最终的理论恢复结果为

CPPPWM系统可以根据自身的脉冲序列形式自动同步。根据式(3)可知，CPPPWM系统若要正确解调需要准确知道ΔTn、Δτn和ΔTn+1三个时间间隔，目的是准确找到系统同步，这样才能够正确解调出信息。不难发现，CPPPWM系统参数m1、m2，d1、d2，K1、K2和F(⋅)就是系统的密钥，只有接收端正确掌握所有参数信息时，才可以正确解调信号。

CPPPWM解调的另一种方式是检测窗法。上升沿和下降沿的检测窗的定义如图3所示。假设解调器一直保持同步，则从混沌脉冲生成器中恢复的脉冲序列将与调制端完全一样，所以图2中第n条脉冲上升沿和下降沿检测时刻和可以确定。上升沿和下降沿的检测阈分别为检测域平均分配给“0”窗和“1”窗，即“0”窗和“1”窗有相同的宽度。由于噪声对于接收信号y(t)造成影响，如果被移动的脉冲沿落入不正确的检测窗就会出现误码，即调制端发送的“0”比特，接收端检测时却落入了“1”窗，反之亦然。本文中，将每个窗分成若干块，每一块的宽度是系统采样周期1/fs，fs为系统的采样频率；接收信号y(t)在检测窗的每一块都被检测一次，即每次采样都被检测一次。

图3 CPPPWM解调器中脉冲检测窗Fig.3 The pulse detection filter of CPPPWM

检测窗法的优点在于对每一个码的检测都是独立的，从而降低了误码率。在仿真时发现，调制逆过程的效果并不理想，这是由于信道中的噪声及多途对接收信号造成畸变与时间扩展，使得对接收信号的初始定位不够准确，进而对接下来的解调产生累积偏差，所以导致误码率较高的情况，采取检测窗的方法来判断解调结果就可以避免累积误差。

1.3 Tent映射下CPPPWM算法

Tent映射与Logistic映射都是经典的一维混沌映射，目前被广泛应用在离散混沌映射系统中。但Logistic映射具有遍历不均匀性，计算速度相对缓慢；而Tent映射结构简单，迭代结构更适合计算机，且Tent与Logistic互为拓扑共轭映射，具有相同的混沌特性，所以Tent映射下的混沌序列在混沌扩频码、混沌保密系统和混沌优选算法等领域中更具优越性[7]。基于上述结论，本节研究了Tent映射下CPPPWM算法的实现。

Tent映射方程：

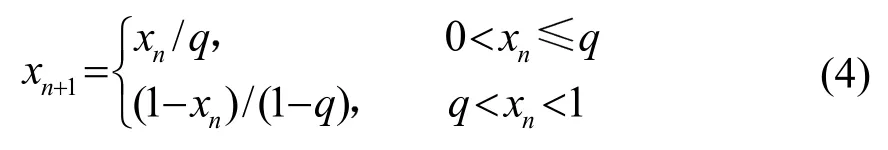
其中，系统参数q∈(0,1)，当参数q在(0,1)区间变化时，系统处于混沌状态；且q=0.5时，系统呈短周期状态，如(0.2,0.4,0.8,0.4…)，系统的结构较为简单，所以q=0.5时混沌系统复杂度最小。另外，Tent系统的初始值不能与系统参数q相同，即x0≠q；否则系统会随时间演变为一个周期系统，丢失映射的混沌特性。所以，使用Tent映射系统时，应合理选取系统参数q和系统初始值x0[8]。

根据1.1节对CPPPWM系统调制的描述，输出值通过函数F(⋅)循环迭代得到。从初始值x0映射到xn的公式如式(5)所示，xi均为[0,1]分布。

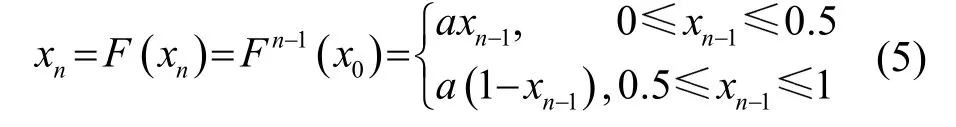
式中，n是时间步长，x0是初始值，xn-1是第n个时刻的输出值，参数a与q呈倒数关系，a控制Tent映射的混沌行为。

在CPPPWM系统中，根据式(4)，第n个脉冲的位置与宽度可重新定义为

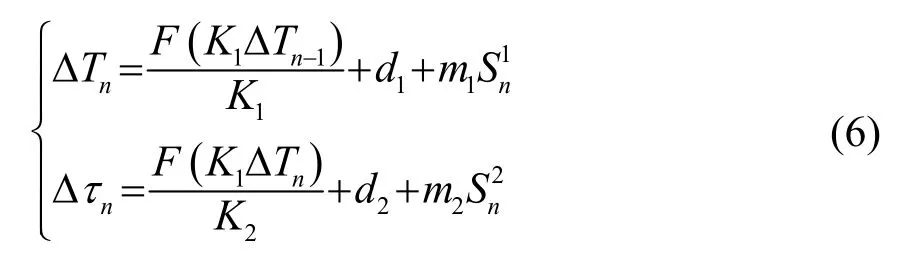
继续对式(6)进行转换，得到

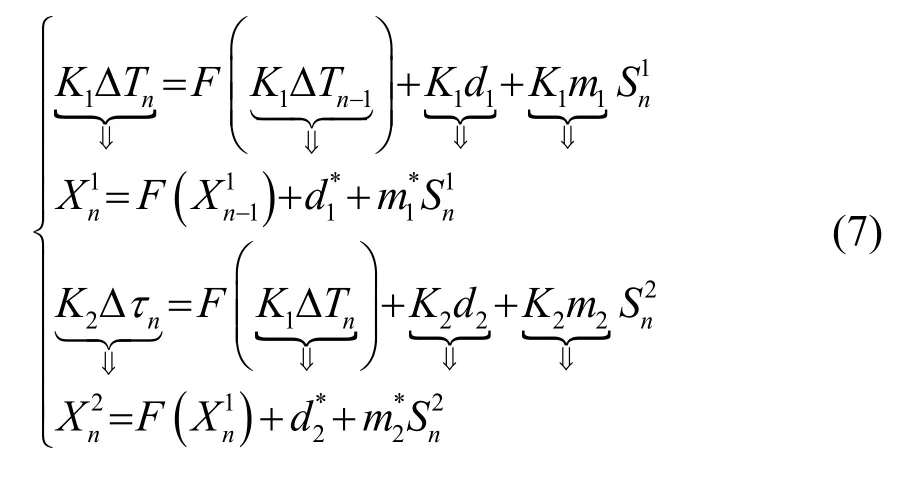
其中，K1ΔTn-1和F(K1ΔTn-1)是非线性函数F(⋅)在第n-1时刻的输入和输出；K1ΔTn和F(K1ΔTn)是非线性函数F(⋅)在第n时刻的输入和输出。为公式推导方便，K1d1用表示，K2d2用表示。K1m1用表示，K2m2用表示。从式(6)中提取出简化的脉冲时间间隔为

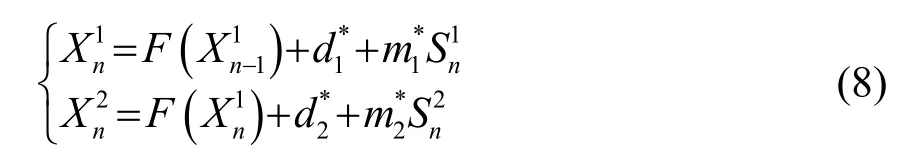
根据式(5)和式(7)可得，基于Tent映射的CPPPWM系统映射可写为

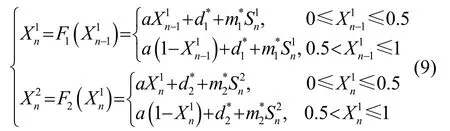
1.4 误码率性能分析

为便于分析，将CPPPWM系统的环境简化为加性高斯白噪声信道，简化后的CPPPWM系统如图4所示。传输信号和信道噪声叠加在一起为阈值检测器的输入，记为y(t)，在阈值检测器中与门限H作对比。当y(t)的量级大于H时，产生相应的脉冲沿，输出端输出幅度为A的矩形脉冲p(t)。阈值检测器的输出被送入CPPPWM解调器以恢复二进制信息[9]。

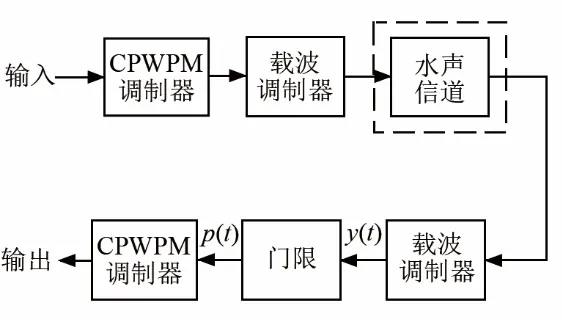
图4 简化CPPPWM通信系统模型Fig.4 Simplified CPPPWM communication system model

一个CPPPWM脉冲包含的一个符号S，每个符号S含有两比特信息“00”、“01”、“10”或“11”。在以下分析中，以符号“00”为例，发送符号S00，那则正确的符号检测概率为

其中，PR0/0是发送“0”上升沿、检测也为“0”的概率，PF0/0是发送“0”下降沿、检测也为“0”的概率。由于PR0/0概率是接收信号y(t)在上升沿任意一个检测窗内都超过门限H的概率，检测窗在高斯白噪声环境下是统计独立的，如果超过1/4的符号解调错误，那么就可以认为信息无法恢复，CPPPWM系统的理论误码率BER的估计如式(11)所示[10]：

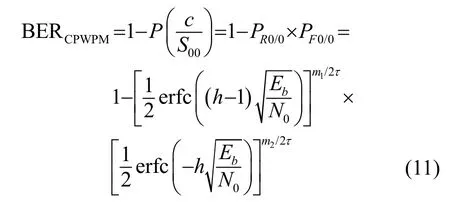
其中，m1/2和m2/2是上升沿和下降沿的检测窗宽度，h=H/A，Eb=A2τ是每比特码的能量，N0=2σ2τ是噪声谱密度，erfc 是互补误差函数。

2 仿真验证

首先给出Tent映射及Tent映射下的CPPPWM通信系统参数理论计算方法，然后在噪声信道下对CPPPWM系统进行仿真，信道噪声采用加性高斯白噪声，最后将理论计算结果与仿真结果作对比，验证CPPPWM通信系统性能，并给出结论。

CPPPWM通信系统的参数选取如表1所示。

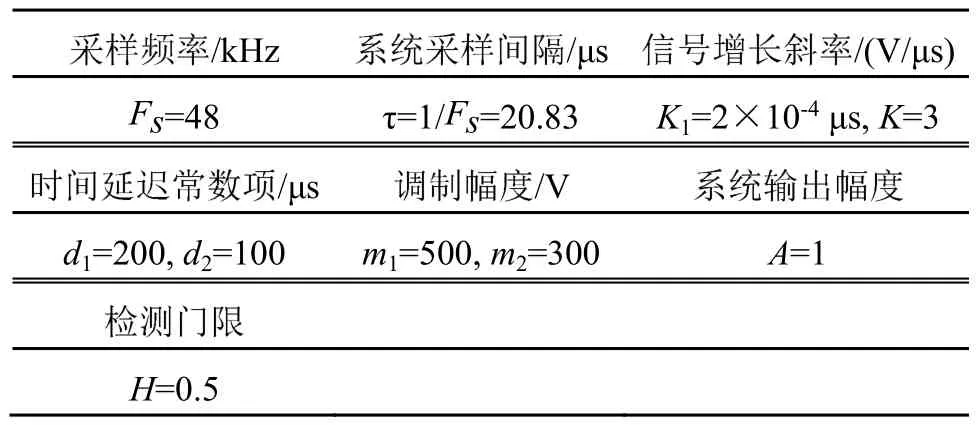
表1 CPPPWM通信系统参数Table 1 Parameters of CPPPWM communication system

由表1中的参数对应CPPPWM系统的理论分岔特性如图5所示，选取系统参数a=1.6，使得该系统的输出混沌值在(0,1)间变化。

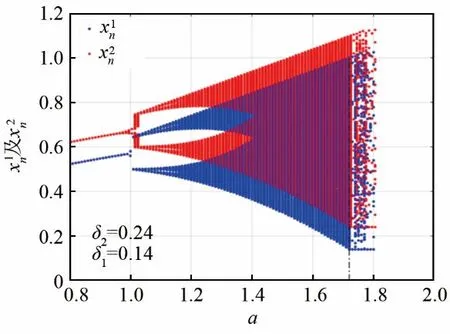
图5 CPPPWM-Tent映射的分岔图Fig.5 Bifurcation diagram of CPPPWM-Tent mapping

Tent映射下的CPPPWM系统参数设计为

由式(12)知道δ1=K1(d1+m1)=0.14，系统维持混沌特性保持不变的条件为1＜a≤2(1-0.14)=1.72，所以可以验证本次CPPPWM通信系统中选择a=1.6是符合系统维持混沌特性条件的。混沌系统平均参数定义为

根据上述理论计算参数，在MATLAB环境下对Tent映射下的CPPPWM通信系统进行仿真，该系统的时域信号仿真如图6所示。从图6中可以发现，只要确定系统保持同步，解调器输出的恢复信号与输入调制器的信号完全相同。

应用仿真数据通过时变信道来验证CPPPWM系统在外场试验的可行性，图7所示为本次验证使用的仿真时变信道，时延为80 ms，时长为1.6 s；发送数据最大带宽为1 502.0598 Hz，平均比特率为627.0909 bps。

图8所示为仿真时变信道下CPPPWM系统的发送与接收解调波形，最终解调结果为100 bit数据中有3 bit误码，误码率量级为10-2。由于时变信道的多普勒效应对脉宽与脉位在时域上产生压缩或扩展影响，导致接收数据码元与参考码元的相关性变弱，引起时间漂移累积。时间漂移会引起系统不同步，进而导致通信误码率增加[11]。

图6 数据输入1和2的CPPPWM时域调制过程Fig.6 CPPPWM modulation performed for input data 1 and 2 in time domain

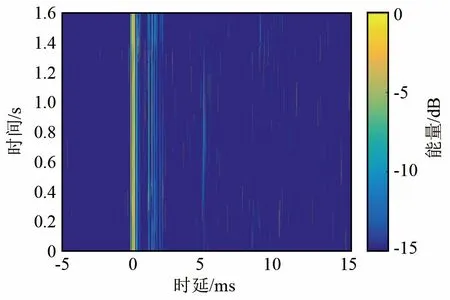
图7 CPPPWM系统实验的仿真时变信道Fig.7 The simulated time varying channel for CPPPWM system testing

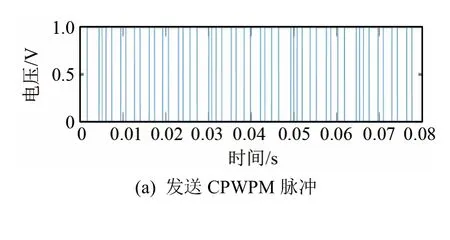
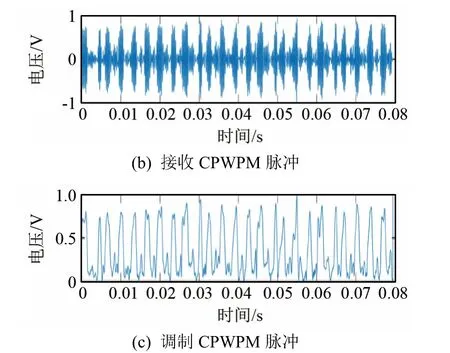
图8 仿真时变信道下CPPPWM系统的发送波形、接收波形和解调波形Fig.8 The transmission,receiving and demodulation waveforms of CPPPWM system in the simulated time varying channel

图9所示为加性高斯白噪声下CPPPWM的理论与仿真误码率特性对比图，总传输码为100 bit。理论误码率采用式(11)，仿真误码率利用检测窗法解调出的数据统计计算得到。

通过图9中仿真条件下的CPPPWM与CPPM误码率对比曲线可知，CPPPWM的系统性能比CPPM系统性能略差。这是由于CPPM解调过程比CPPPWM简单，只需要恢复一组混沌序列，而CPPPWM则要解调两组混沌序列，虽然两组混沌序列并不相干，但误码率会累积增大。作为补偿，CPPPWM系统的通信速率较CPPM有大幅度提升。图9中的CPPPWM理论与仿真误码率对比曲线显示，当信噪比(SNR)在12 dB以下时，系统的仿真误码率要高于其理论误码率；当信噪比大于12 dB时，理论与仿真误码率结果趋于一致。目前认为其原因是在理论分析时，我们假设前提为系统永远保持同步，所以误码仅由对脉位与脉宽的错误判断产生，也就是说误码仅由噪声引起[12]；而在仿真过程中，信号畸变是信道中加入的高斯白噪声造成的，这种信道畸变会影响脉位与脉宽的长度，进而使通信系统丢失同步，造成误码。但随着信噪比增加，系统同步性变好，仿真的误码率结果就会趋近于理论分析的结果。

图9 理论计算和仿真实验得出的CPPPWM系统误码率曲线，CPPPWM与仿真实验得出的CPPM系统误码率曲线Fig.9 BER characteristics of CPPPWM system obtained from theoretical calculation and simulated test,CPPPWM and the BER characteristic of CPPM system obtained from simulated test

3 结 论

本文论述了一种混沌脉宽与混沌脉位联合调制通信的方法，并在Tent映射下对CPPPWM系统性能加以验证，对系统误码率进行分析。CPPPWM调制下每一个脉冲可以承载2 bit信息，所以通信速率较传统的PPM、PWM以及CPPM调制方式提高到两倍。CPPPWM技术生成的信号具有脉冲串的形式，所以该信号不需要发送端另外加入同步头，可以在接收端进行自同步，这样的调制方式即使在畸变的信道下仍可以保持良好的通信性能，具有通信保密性。CPPPWM技术中脉宽信息与脉位信息的调制解调是相互独立的，所以CPPPWM技术可以用于双用户通信技术中。CPPPWM技术在误码率性能上较扩频通信稍差，但具有低截获率、低破解率的特点，且通信系统保密性好、通信速率快、可用于多用户通信[12]。CPPPWM系统本身具有很好的系统同步性，但其本质是基于脉宽与脉位调制的，在继承脉宽脉位调制抗干扰能力的同时，也为该调制方法带来对多普勒效应敏感的特点。所以在系统解调过程中出现系统同步偏差进而导致误码率升高，对于减小CPPPWM解调过程造成的系统定位偏差问题，今后可考虑采用多普勒容限较高的混沌编码映射以及多普勒补偿的办法，以上改进办法的有效性有待进一步研究。