以简正波解为初始场的抛物方程算法应用于深海声传播预报

肖 瑶，唐 骏，张 鹏，李整林

(1.中国科学院声学研究所声场声信息国家重点实验室，北京 100190；2.中国科学院大学，北京 100049；3.哈尔滨工程大学水声技术重点实验室，黑龙江 哈尔滨 150001；4.哈尔滨工程大学水声工程学院，黑龙江 哈尔滨 150001)

0 引 言

声波在深海中的传播规律是深海目标探测的重要基础。要探索和总结深海声传播规律，前提是要对深海声场进行准确预报。

目前广泛应用的海洋声场预报方法主要有简正波方法[1]，耦合简正波方法[2]，射线法[3]，抛物方程方法[4-5]，波数积分法[6]等。在深海中，环境参数不仅在深度上起伏变化，在水平方向上也会因内波、涡旋、锋面、洋流等现象而发生变化。简正波方法和波数积分法仅适用于水平方向环境参数不变的波导，故不适用于深海声传播预报。耦合简正波方法、抛物方程方法和射线方法适用于深海中环境参数同时随距离、深度变化的波导。这三种方法各有优缺点。耦合简正波方法的优点在于具有清晰的物理意义，但缺点是耦合系数的计算较为复杂，且目前公开的耦合简正波程序COUPLE存在模态阶数的限制，对于深海声传播这样具有上千阶模态的问题难以保证计算精度。射线法具有清晰的物理意义，由一系列从声源出发的声线经过海底、海面反射后到达接收点，而接收点处的总声场为各条声线所贡献的声场之和；不过射线法的缺陷在于难以计算声影区内的声场。抛物方程方法的优点在于能够便捷地处理与深度、距离有关的声速、地形等环境，是一种随距离逐步递推的数值方法，其缺点是缺乏清晰的物理意义。综上所述，对于深海声传播的预报，如何得到一种物理意义明确、同时又计算简便的方法，仍是一个值得进一步探讨的问题。

McDaniel在分析早期抛物方程法的误差时曾采用抛物方程法对单阶简正波的声场进行递推[7]。Zhou等[8]使用此方法分析过浅海中内波影响下的各阶简正波耦合特点与能量变化。此外，徐传秀等[9]实现了利用简正波解为三维抛物方程方法构造初始距离处的声场(初始场)。受此启发，本文将此方法应用于深海声传播的预报。首先，利用简正波解构造初始场，然后用抛物方程法对初始场进行递推，最终得到深海波导全空间中的声场。若仅采用初始距离处的某一阶简正波作为初始场，还可观察到该阶简正波的能量在整个远距离传播过程中的变化情况。由此可以看出，此方法兼具物理意义明确和计算简便的优点。

本文首先给出以简正波解作为初始场的抛物方程法的理论公式，其次对该方法的数值结果进行验证，然后将该方法应用于涡旋影响下的深海远程声传播问题，并分析了涡旋对单阶简正波能量传播的影响。

1 理 论

抛物方程法的基本原理是用变量分离方法将声场分解为水平分量，而垂直分量控制方程采用算子分解的近似方程转化为抛物方程，再用数值方法直接求解该抛物方程。

1.1 抛物方程Ram模型理论基础

自Tappert提出抛物方程(Parabolic Equation,PE)标准以来，已经发展出多种PE方法。具有代表性的是COLLINS M D提出宽角PE模型，相应的数值计算软件称为Ram[4,10-11]。由于其使用分步Padé近似求解抛物方程，其计算速度和计算精度较以往的PE模型有了很大的提高，因而得到了广泛应用。下面给出推导过程[11]。从波动方程出发：

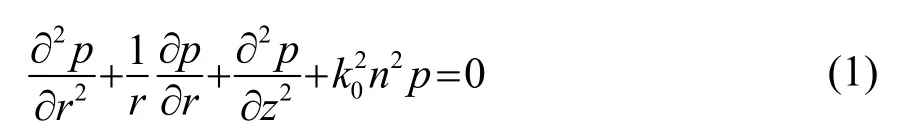
其中，k0代表设定初始波数，选取解的形式为

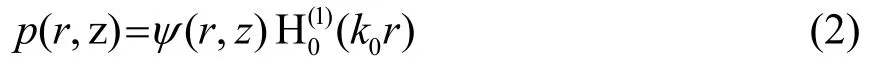
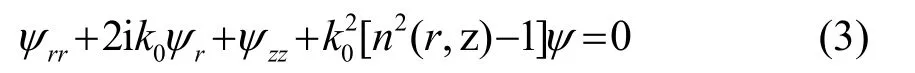
对式(3)进行因式分解，得到广义算子形式的表达式为

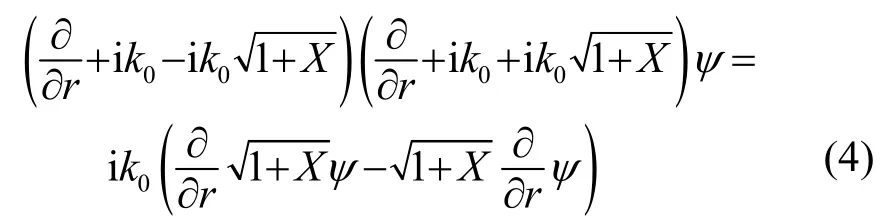
其中：

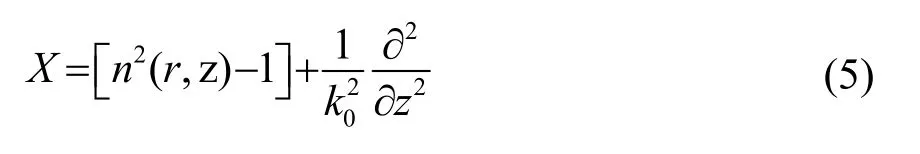
在n(r,z)与距离的关系足够弱时，可以忽略换位子项，只选择输出波分量，得到

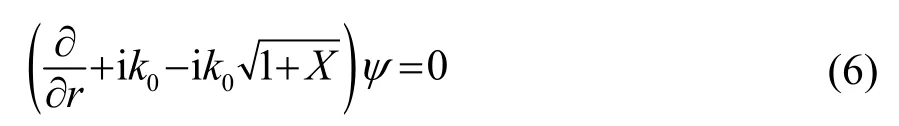
结合式(4)～(6)求解后得到

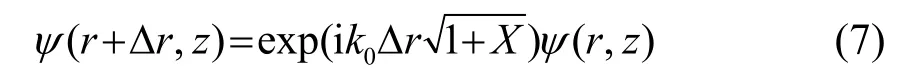
Δr表示步长，使用Padé近似后给出解的形式如下：

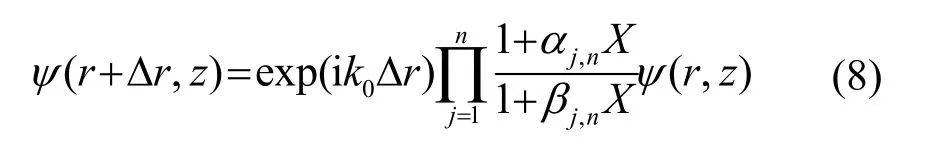
其中，αj,n和βj,n为Padé系数。利用COLLINS M D给出的Galerkin离散公式[11]，对将上述方程离散成矩阵形式，进而根据r处声场解出r+△r处的声场。

1.2 简正波初始条件

Ram里面使用的是自初始条件[10-11]，虽然自初始条件是一种高效且较准确的产生初始场的方法，但是自初始条件产生的是全初始场，缺乏清晰的物理意义，下面构造简正波初始场。在推导归一化简正波初始条件表达式之前，首先将式(1)简化，将声压p(r,z)和包络函数ψ(r,z)联系起来：

使用简正波求解声压表达为

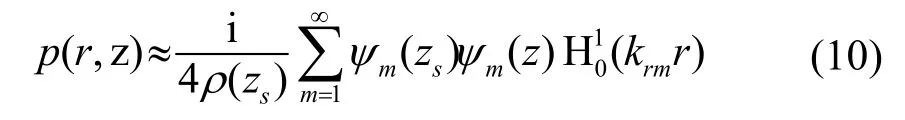
krm和Ψm(z)分别表示第m阶简正波的水平波数和本征函数，采用汉克尔函数的渐近式为

自由空间中点源的声压为

由式(11)和式(12)求得归一化简正波场为

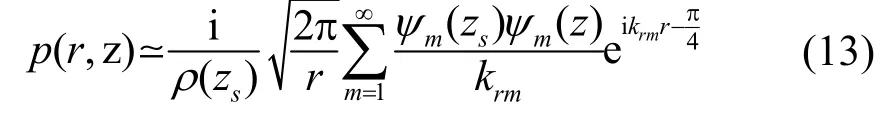
将式(13)代入式(9)中，即可得出ψ在r=Δr处的归一化初始场。

2 模型验证

图1 水平不变环境下海洋环境示意图Fig.1 Range-Independent Ocean Environments

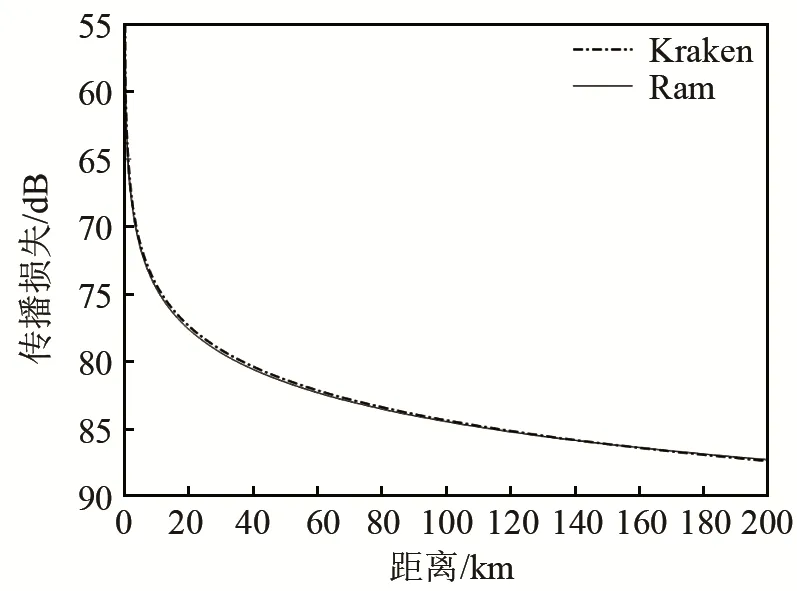
图2 水平不变情况下1号简正波声传播损失Fig.2 The first normal mode transmission loss under rangeindependent environment

第1节中给出了理论推导，首先利用Kraken求出简正波解来构造初始场，然后使用抛物方程法Ram对初始场进行递推，最终得到深海波导全空间中的声场。本节在水平环境不变的条件下验证模型的可行性与准确性。海洋环境如图1所示，海水密度为1 000 kg·m-3，水深为4 500 m。海底为半无限空间，声速为1 650 m·s-1，密度为1 800 kg·m-3，海底衰减系数为0.175 dB·λ-1。声源频率为50 Hz，声源深度为800 m，当接收器深度为800 m时，Kraken计算的第1号简正波的传播损失曲线和Ram计算结果一致，如图2所示。图3(a)和图3(b)分别为Kraken和Ram计算1号简正波的二维传播损失彩图。由此可知，使用简正波初始条件结合Ram抛物模型计算各阶简正波的能量传播情况是有效且准确的。

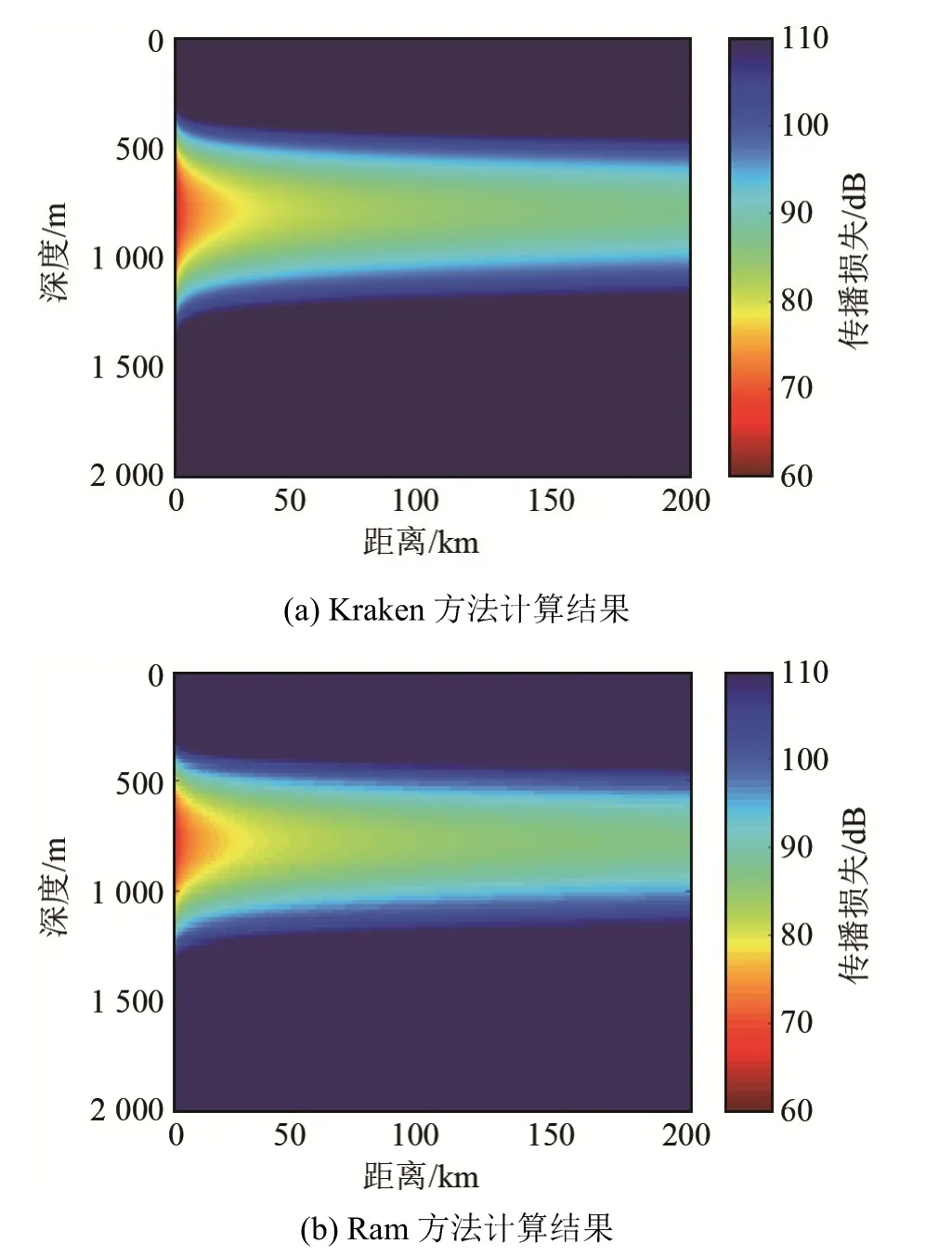
图3 水平不变情况下1号简正波声传播损失二维彩图Fig.3 The first normal mode transmission loss under rangeindependent environment

3 中尺度涡影响下深海声传播问题

由第2节中的结果表明，以简正波解作为初始场的抛物方程法，对于计算深海中某一阶或某几阶简正波的能量传播过程是有效的。本节将该方法应用于涡旋等复杂海洋情况下的深海远程声传播问题，并分析了涡旋对单阶简正波能量传播的影响。

假设在图1所示的海洋环境中，在150 km处存在一个半径为150 km、影响深度为1 600 m的冷涡旋。由于涡旋的影响，声速产生扰动，图4为存在涡旋时的等声速图。设声源频率为50 Hz，声源深度为1 000 m。

图5为接收深度为1 000 m时，当存在涡旋时的传播损失与没有涡旋时的对比，图6为此环境下第1号简正波的传播损失二维彩图。由图5和图6可知，此种方法非常直观地展示了各号简正波能量传播路径的变化。这里由于涡旋对海洋环境的扰动，使第1号简正波的能量传播路径逐渐向上移动了几百米，能量耦合到了其他号简正波上。能量传播路径的变化与相应位置的简正波特征函数曲线对应，如图7所示。图8中选择前10号简正波作为初始场进行了计算，由结果可知，这10个简正波的总和同样受到了涡旋的强烈影响，能量传播路径整体向上偏移，传播路径弯曲度最大的地方发生在冷涡旋中心位置附近。经过分析可知，在深度为400～2 100 m的接收深度范围内，前10号简正波占了绝大部分能量，简正波号数越大，所受到涡旋的影响越小，所以使用此方法可以更加深入具体地分析涡旋等复杂海洋环境中的能量传播与耦合情况。

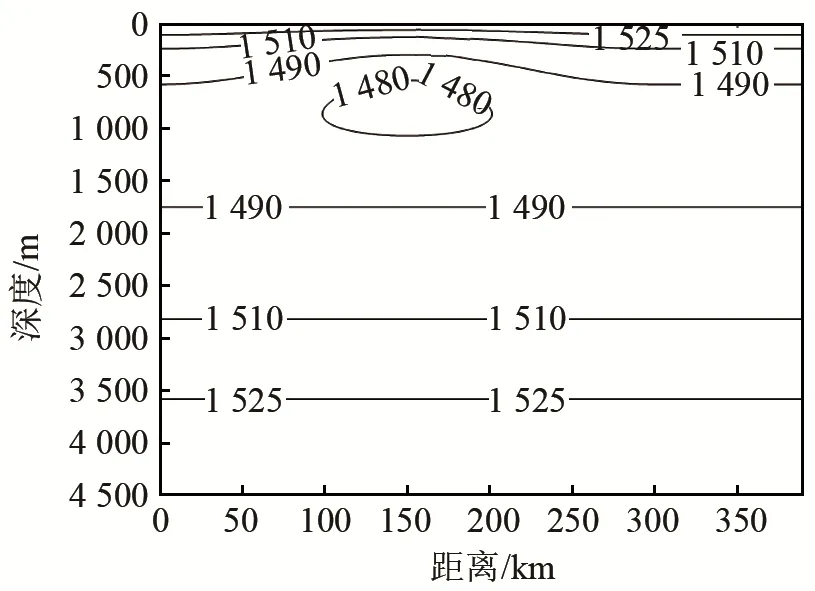
图4 存在涡旋时的等声速图Fig.4 Numerically computed isospeed curves for a mesoscale eddy

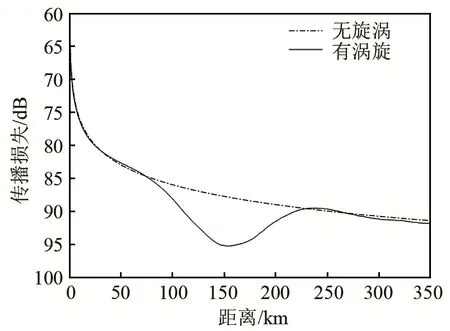
图5 无涡旋与有涡旋海洋环境下第1号简正波传播损失Fig.5 Comparison of 1 000 m transmission loss between the environments with eddy and without eddy

图6 无涡旋与有涡旋情况下1号简正波声传播损失二维彩图对比Fig.6 The first normal mode transmission loss under the environment with eddy or without eddy

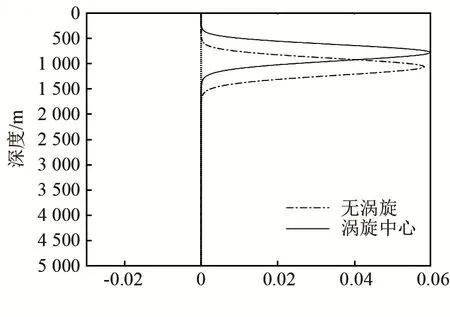
图7 有涡旋时与没有涡旋时1号简正波对比Fig.7 Comparison of the first normal mode between the environments with eddy and without eddy

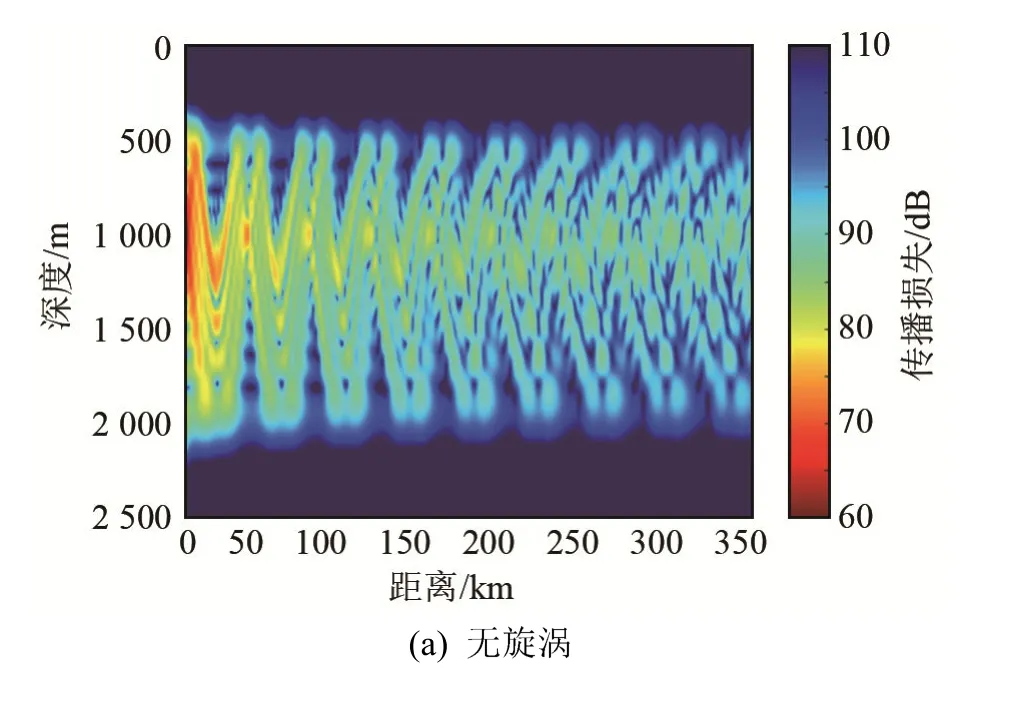
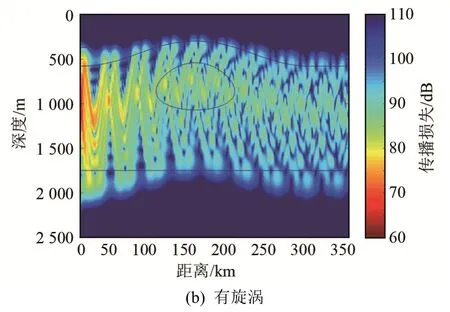
图8 无涡旋与有涡旋情况下1～10号简正波声传播损失二维彩图对比Fig.8 The first ten normal mode transmission losses under the environments with and without eddy

4 结 论

本文首先推导以简正波解作为抛物方程法的初始场的理论公式，然后通过数值仿真证明了该方法的有效性，最后再将此方法应用于分析涡旋等复杂海洋环境下的远程声传播预报，并分析了涡旋对单阶简正波传播的影响。结果表明，本方法可以应用于求解水平不变以及复杂的海洋变化环境下的声传播问题，不仅可以获得比较高的准确度，而且有比较高的计算效率。更重要的是，相对于抛物方程法，本方法具有非常清晰的物理意义。同时，使用本方法计算某阶或某几阶简正波的能量传播，再结合射线理论进行分析，对深入研究中尺度涡旋等复杂海洋环境下的声传播特点与能量变化关系具有重要作用。