均匀海洋波导本征值问题的多模态分析方法
2019-05-21魏旺,王斌,范军
魏 旺,王 斌,范 军
(上海交通大学高新船舶与深海开发装备协同创新中心,海洋工程国家重点实验室,上海 200240)
0 引 言
简正波理论[1]是用来分析波导中声传播准确解的常用方法,在单层等声速波导中通常能够得到本征值和本征函数的解析式从而简化计算。但在一些复杂的情况下(例如具有声速剖面的波导、双层波导),由复杂边界带来的超越方程的搜根问题,使得本征值、本征函数的计算量很大。目前已有的常用的方法有图像法、牛顿迭代法等,但这些方法的计算速度慢,精度低,且会受到设定初值的影响,从而产生丢根和漏根的情况。为了提高本征值的求解效率,谱方法[2]被应用于求解波导中的超越方程,避免了传统搜根法带来的漏根,且具有较快的收敛速度,其中较为常用的是切比雪夫(Chebyshev)多项式进行迭代计算,但该方法在某些参数选取不恰当时带来的收敛性并不理想[3]。
PAGNEUX等[4]、BI等[5]在计算声管中的声传播时提出了多模态方法(Multimodal Approach,MA),用正弦或者余弦函数作为谱方法中的正交基,求解出声管中的本征函数,比搜根法具有更高的效率。虽然与切比雪夫多项式相比,多模态方法需要更高的截断阶数,但其结果总是收敛的,在不同边界条件下的均匀、非均匀波导中都具有一定的应用前景。
本文将该方法推广至海洋波导中,将超越方程的搜根问题转化为正交展开系数矩阵的特征值分解。计算了单层及双层波导的本征值与本征函数,通过与解析解以及简正波程序KRAKEN的结果对比,验证了该方法的有效性,为进一步研究均匀、非均匀波导中的声传播提供了新的思路。
1 均匀海洋波导中的多模态方法
如图1所示的轴对称均匀波导中,水平和深度方向分别是r轴和z轴,假设海面位于z=0处,海底位于z=h处。海底以下直到H是沉积层。波导中海水声速cw(z)在竖直方向上连续变化,密度为常数ρw,沉积层的声速和密度分别为常数cb和ρb。
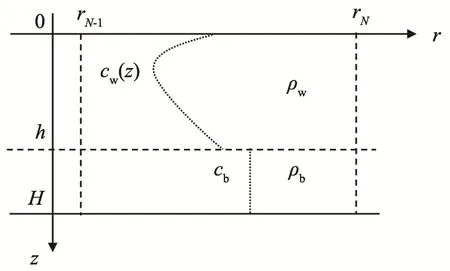
图1 均匀波导模型Fig.1 Model of the homogeneous waveguide
波动方程的柱坐标表达式为[1]
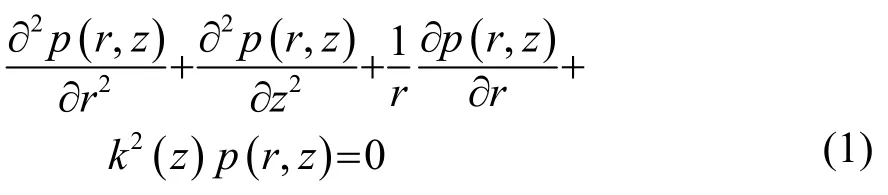
其中:k(z)=2πf/c(z),c(z)在海水和海底中分别记为cw(z)和cb;f为声源频率;p代表声压,其满足海面自由、海底处声压和法向振速的连续条件:
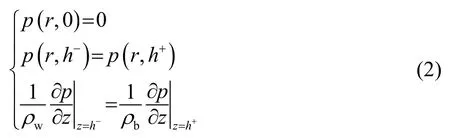
假设y=H处为刚性边界,即

通常情况下,根据式(2)的前两个条件,可以设本征函数具有式(4)的形式[6]
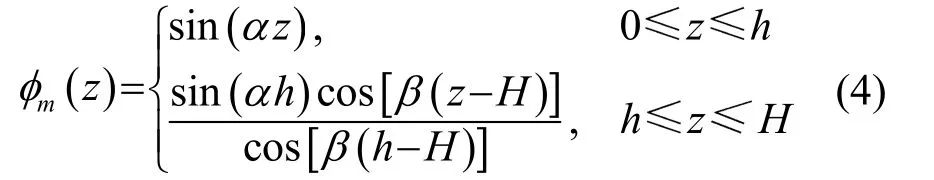
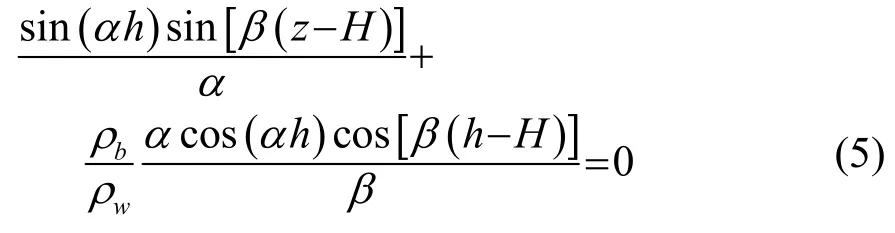
因此,本征方程的求解转化为对超越方程(5)的搜根问题。一般的解法有图像法、牛顿迭代法等,但这些方法速度慢、精度不高且依赖于初值。因此这里引入多模态展开方法[7],令:
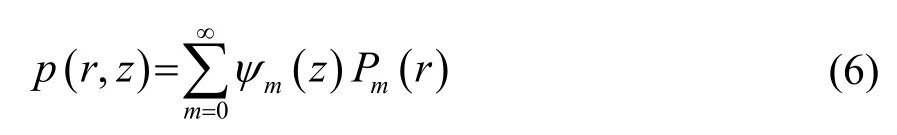
式中,Pm(r)为不同阶的展开系数。正交函数ψm满足
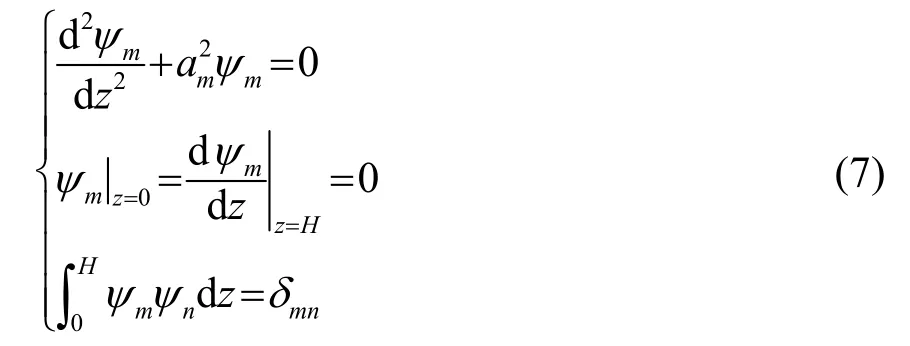
其中:

设mψ具有如式(4)所示的形式:
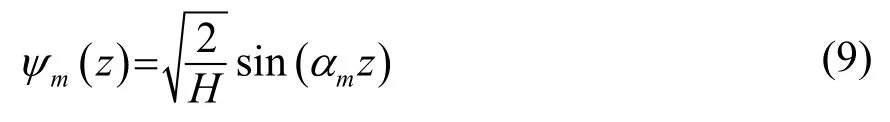
其中:

使用正弦函数的优势在于,其任意阶导数都具有解析表达式,避免了数值发散(例如使用切比雪夫多项式[2])。计算时,通常取m=0,1,⋅⋅,M-1的前M阶进行截断,即

其中,Ψ(z)是由正交函数ψm(z)组成的M元列向量,上标T表示转置,P(r)表示不同阶的展开系数Pm(r)组成的M元列向量。

其中,P′′(r)、P'(r)分别表示由组成的列向量,A是M×M维矩阵:
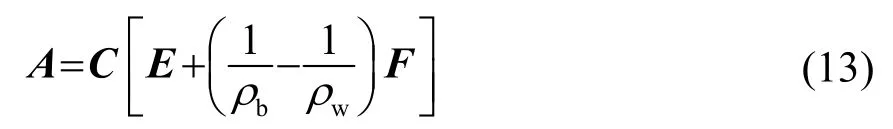
矩阵C、F、E中的元素分别为
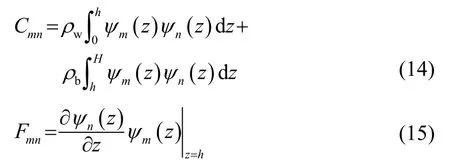
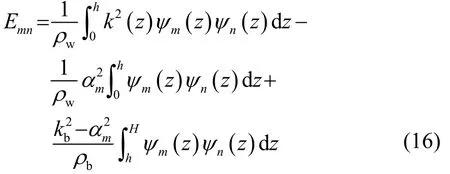
矩阵A经特征值分解得到

其中,Λ代表矩阵A的特征值dm组成的对角阵。X代表特征向量组成的列矩阵。
根据式(12)与式(17)可以得到
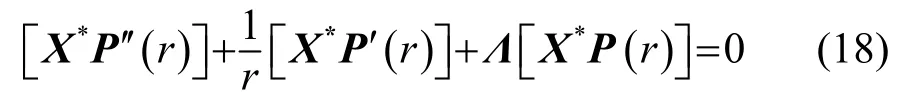
式(18)为零阶贝塞尔方程,其具有通解形式
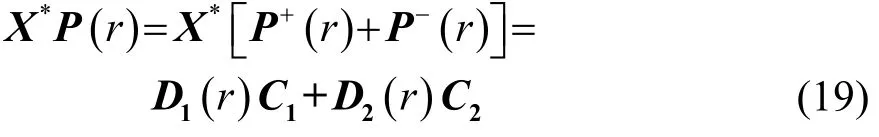
其中,+、-分别表示向外、向内传播的分量。D1和D2分别满足:
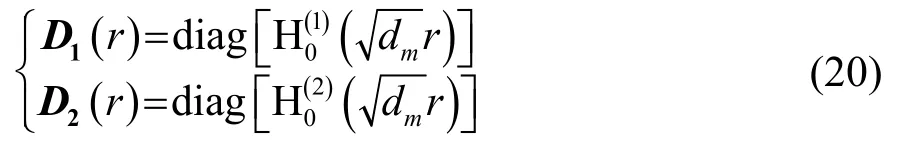
对于二维波导情况,距离和深度方向分别为x和y轴,波动方程满足:
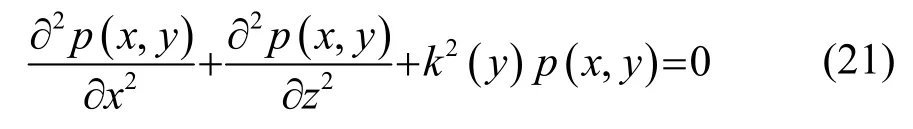

其通解为
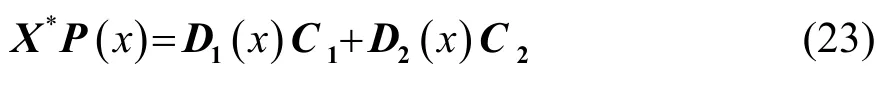
其中:

关于本征值的超越方程搜根问题被转换为矩阵的特征值问题,同时可以得到本征函数,因此尤其适合于本征函数无解析表达式的情况。
2 数值验证与分析
本节分别给出多模态方法在单层等声速波导、具有声速剖面的波导以及双层波导的本征值与本征函数计算结果,并与一些标准结果进行对比验证,其中通过本征函数(振型)的分布可以看出各个模态的传播规律。
2.1 单层波导的本征值与本征函数
单层等声速波导中,设水中密度ρw=1 000 kg·m-3,海底为水平边界,水深H=500 m,分析频率为25 Hz,等声速情况下设其声速cw=1 500 m·s-1为常数。由于是单层波导,令双层模型中的ρb=ρw,ρb=ρw,即h=H,具体推导过程不再重复。
等声速情况下,波导中的声场分布情况可以写成解析解的形式[8],其中本征值可以表示为
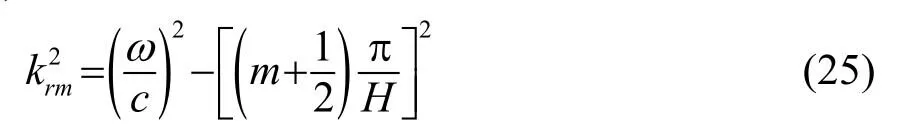
表1给出了解析解与多模态展开方法的计算结果,由于单层波导中的本征方程及其导数有较好的连续性,因此用较低的模态阶数即可得到较为准确的计算结果,这里将截断阶数选取为16。

表1 等声速波导本征值Table 1 Eigenvalues of isovelocity waveguide
本征函数如图2所示,可以看到多模态方法的本征值、本征函数计算结果与解析解具有很好的一致性。
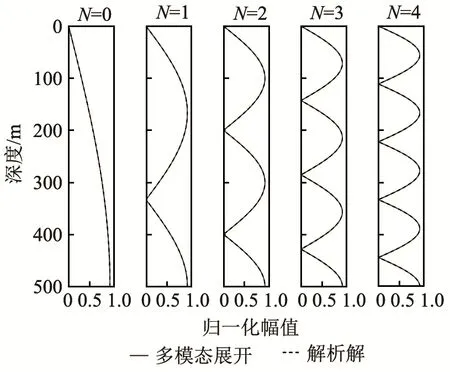
图2 等声速波导本征函数Fig.2 Eigenfunctions in isovelocity waveguide
当波导中随深度方向具有声速剖面时,假设该声速剖面如图3所示,声速剖面的表达式为[9]
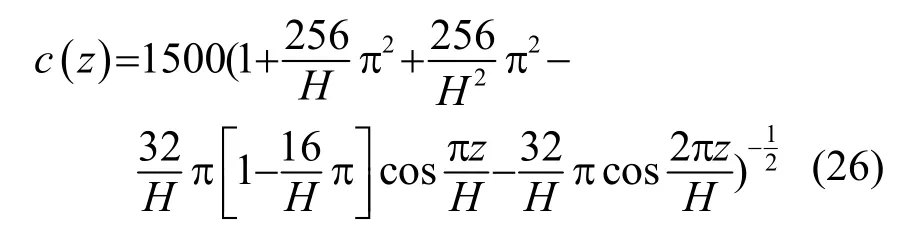
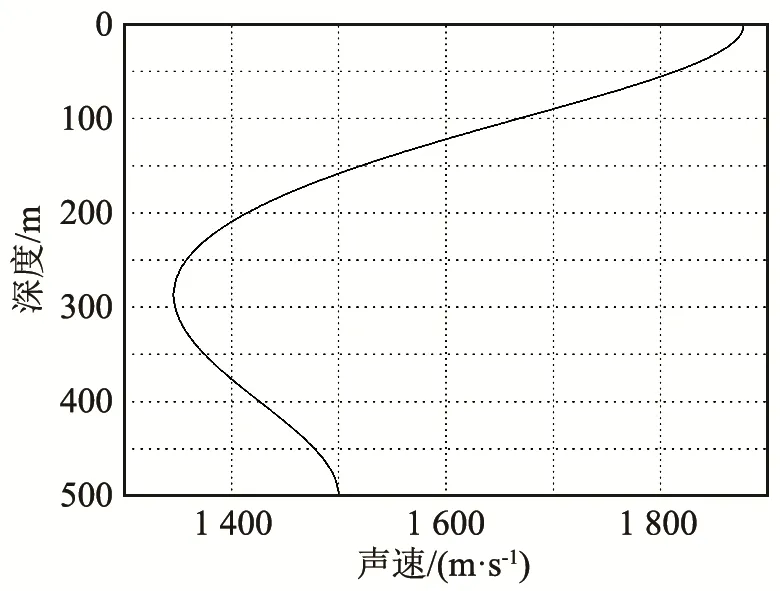
图3 声速剖面示意图Fig.3 A typical sound velocity profile
在具有声速剖面的情况下,本征值和本征函数没有解析解,因此可以通过数值方法进行计算,这里将KRAKEN计算程序的数值结果作为标准解与多模态展开方法进行比较,波导中除声速外其他参数与等声速情况一致,其本征值计算结果如表2所示。在同样的计算机运行环境中,KRAKEN方法的计算时间为0.342 s,多模态展开算法的计算时间为0.017 s。另外,通过观察本征值的数量级可以知道,相邻模态的本征值之差很小,这就对搜根法提出了更为严格的要求。若搜根的步长过大,很容易产生漏根,若步长过小,则会产生较多重根,从而导致计算效率的降低。本征函数结果如图4所示,可以看到两种方法的计算结果相吻合。另外,通过对比图2与图4可得,等声速情况下本征函数在深度方向上均匀分布,而在具有声速剖面时,低阶模态主要集中在低声速区域传播。
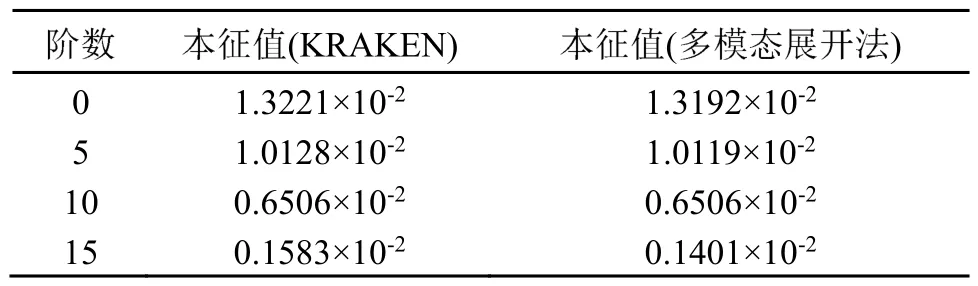
表2 变声速波导本征值Table 2 Eigenvalues in the waveguide with sound velocity profile
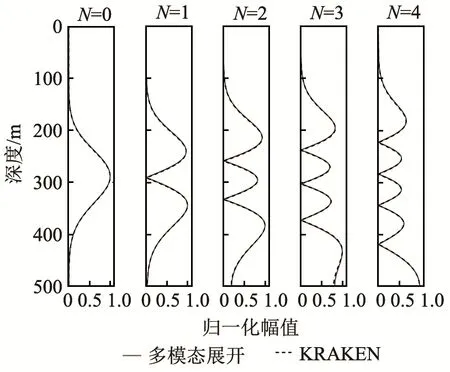
图4 变声速波导本征函数Fig.4 Eigenfunctions in the waveguide with sound velocity profile
2.2 双层波导的本征值与本征函数
下面讨论双层波导的本征值与本征函数。分层波导中的本征值与本征函数依然没有解析解的形式。设总深度H=2 000 m,水深h=100 m,水中声速为cw=1 500 m·s-1,密度为ρw=1 000 kg·m-3,海底沉积层中的声速为cb=1 700 m·s-1,密度为ρb=1 000 kg·m-3。由于本征函数的导数在海底界面处的不连续性,通常需要较高的模态截断阶数进行计算以得到可靠结果。这里将模态的截断阶数取为200,表3给出了两种方法得到的本征值,其中KRAKEN计算时间为0.371 s,多模态展开算法的计算时间为0.061 s。本征函数结果如图5所示,可以看到,不同的深度上各阶模态的主要传播区域有所不同,只有前2阶模态主要在水中传播。

表3 双层波导本征值Table 3 Eigenvalues in double-layered waveguide
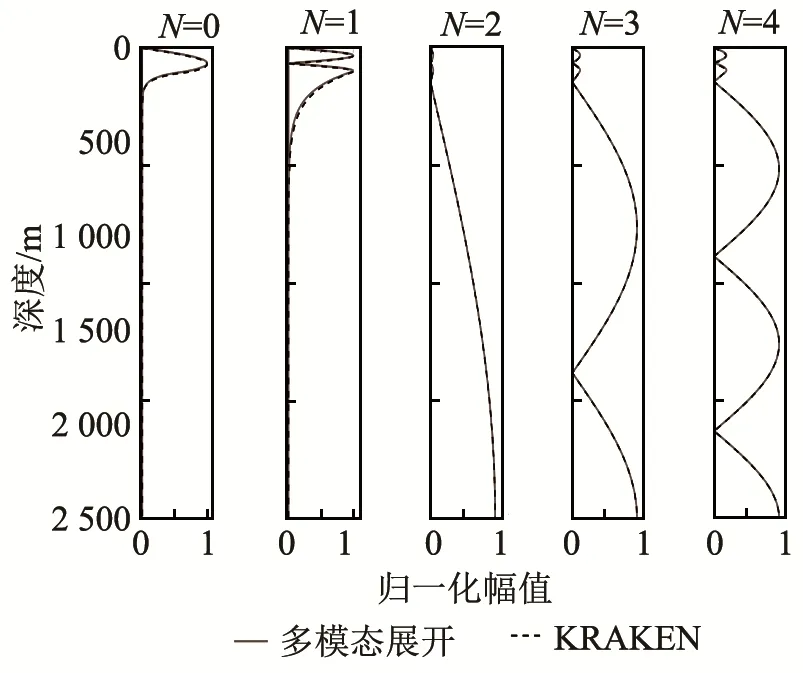
图5 双层波导本征函数Fig.5 Eigenfunctions in double-layered waveguide
3 结 论
本文提出了海洋波导中本征值、本征函数求解的多模态展开方法,将本征函数用正弦函数作为正交基进行展开,将关于超越方程的搜根问题转化为展开系数矩阵的本征值求解问题,从而避免了传统方法求解速度慢、需要设定迭代初值等缺点。由于正弦函数具有无穷阶的可导性,因而可以保证结果的收敛性。另外,若将该方法用于海底无限深的声学半空间模型,需引入海底吸收并保证底部边界具有足够的深度。本文通过数值计算,验证了该方法在求解等声速波导、声速剖面波导以及分层均匀海洋波导中本征值与本征函数的准确性,为分析均匀、非均匀海洋波导的声传播问题提供了新的思路。
