物流配送路线优化粒子群改进算法

陈 艳

(池州学院 机电工程学院，安徽 池州 247000)

物流配送路线优化的主要目标是确定最优的配送路线，使得配送时间总和最少，总成本最省，它是物流运输中心经营中一个至关重要的问题[1]。如今世界市场的现代物流产业竞争日趋激烈，运输配送时间和成本的控制，成为物流企业赢得市场和利润的关键因素之一。运输配送路线优化问题受众多的因素影响，如何在这些因素之间进行权衡越来越受到研究人员的关注。随着物流企业日渐增长的现实需求，过去被应用到物流配送路线优化的传统算法表现效率较低，渐渐地不能够适应现代物流配送企业需求。

物流中心配送路径优化需要考虑的最重要的两个因素是配送时间和配送成本，想要同时兼顾两个因素，需要优化能力极强的优化方法。目前，研究人员已经有大量的优化方法用来解决物流运输中心配送路径优化选择问题。针对冷链物流网络的网点布局和运输问题,张文峰等提出了一种非线性混合整数规划模型，该模型是基于冷链物流的网点建设成本和运营成本为优化目标，采用量子粒子群算法求解[2]。为了优化车间的物料运输配送路径,杨家平等建立一种数学优化模型，该模型是基于车间物流通道节点,采用新型的单亲遗传算法用于求解[3]。针对物流配送过程中的不同交通环境和工具，以及不同的配送路径,叶威惠等采用改进的遗传算法解决物流运输配送过程中的两个层次的路径优化[4]。考虑到快递和物流配送的异同,麻存瑞等在物流配送路径优化问题的基础上，建立了符合快递配送路径优化问题的数学模型，并基于此设计了一种采用自然数编码,综合考虑快件数量、车辆载重、车辆容量等约束的解码方式的遗传算法[5]。针对传统资源调度算法中资源利用率低等缺点，以上方法能够一定程度的解决配送优化的相关问题，但该算法依然有进一步改进的空间。

物流运输中心配送路径优化问题的求解往往令人不甚满意。这主要有两个方面的原因：一方面是物流中心配送路径优化问题的优化模型较难，不容易寻到满意的优化解；另一方面则是因为现有的优化算法及其改进策略大多存在着一些缺陷，使得其优化达不到预期效果。为了切实有效改善现有优化算法的优化性能，需要针对性地对其改进。因此，为使粒子群方法达到全局收敛的目的，本文在惯性权重粒子群算法的基础上，加入了混沌随机数扰动，并在进化过程中随机给出相应的加速度系数，从而达到改进粒子群优化方法的目的，使粒子群算法的优化性能有效改善。本文基于3种测试函数和1个物流运输中心配送路线优化问题的实际算例，对3种不同的粒子群算法进行了优化性能上的比较，其试验结果说明了本文提出的粒子群改进算法的优化能力更强，能有效解决物流运输中心配送路线优化问题。

1 物流运输中心配送路线优化问题的数学模型

基于实际情况，本文考虑了多个物流中心、多种资源下的多辆配送车辆的配送场景。其主要运输需求如下：

(1)n1种不同资源；

(2)空间上分布着n2个物流中心；

(3)空间上分布着n3个客户，客户对不同资源有不同需求；

(4)尽可能的使得配送时间总和最少和配送成本总和最少，最大配送时间不超过一定数值。

配送路线优化问题的核心是节约其配送成本和配送时间。因此，配送路线优化问题的优化目标有两个，配送时间总和和配送成本总和，记为Tsum和Csum。具体的以配送时间总和和配送成本总和作为优化目标的优化模型为[6]：

(1)

(2)

式中，用l={1,2,3,…,n1}表示资源集合，包含n1个不同的资源；用i,j={1,2,3,…,n2+n3}表示节点集合，包含n2+n3个节点，不包括物流中心和客户；Ci,j和Ti,j表示第i个节点在第j个节点的配送成本和配送时间。若车辆k完成从节点i和j的配送，xi,j,k=1；否则，xi,j,k=0。若节点i的配送由车辆k完成，yi,k=1；否则，yi,k=0。约束1为车辆的载重限制，每辆车的每一种资源的配送总量不得超过车辆该资源的最大载重量；约束2保证每个客户只由一辆车辆负责配送一次，不能重复配送；约束3和约束4则保证所有物流中心和客户都被配送到。目标1和目标2表示该配送优化问题的优化目标是配送时间总和Tsum和配送成本总和Csum。由上述物流中心配送优化问题的优化模型可知，该问题的解不易得到。

2 改进的粒子群算法

2.1 基本粒子群算法

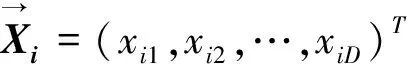
(3)

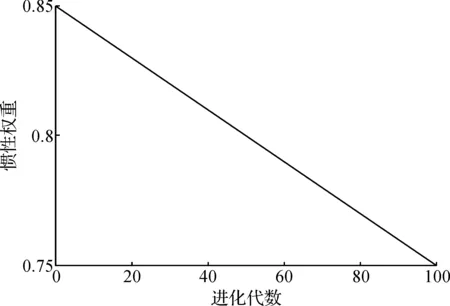
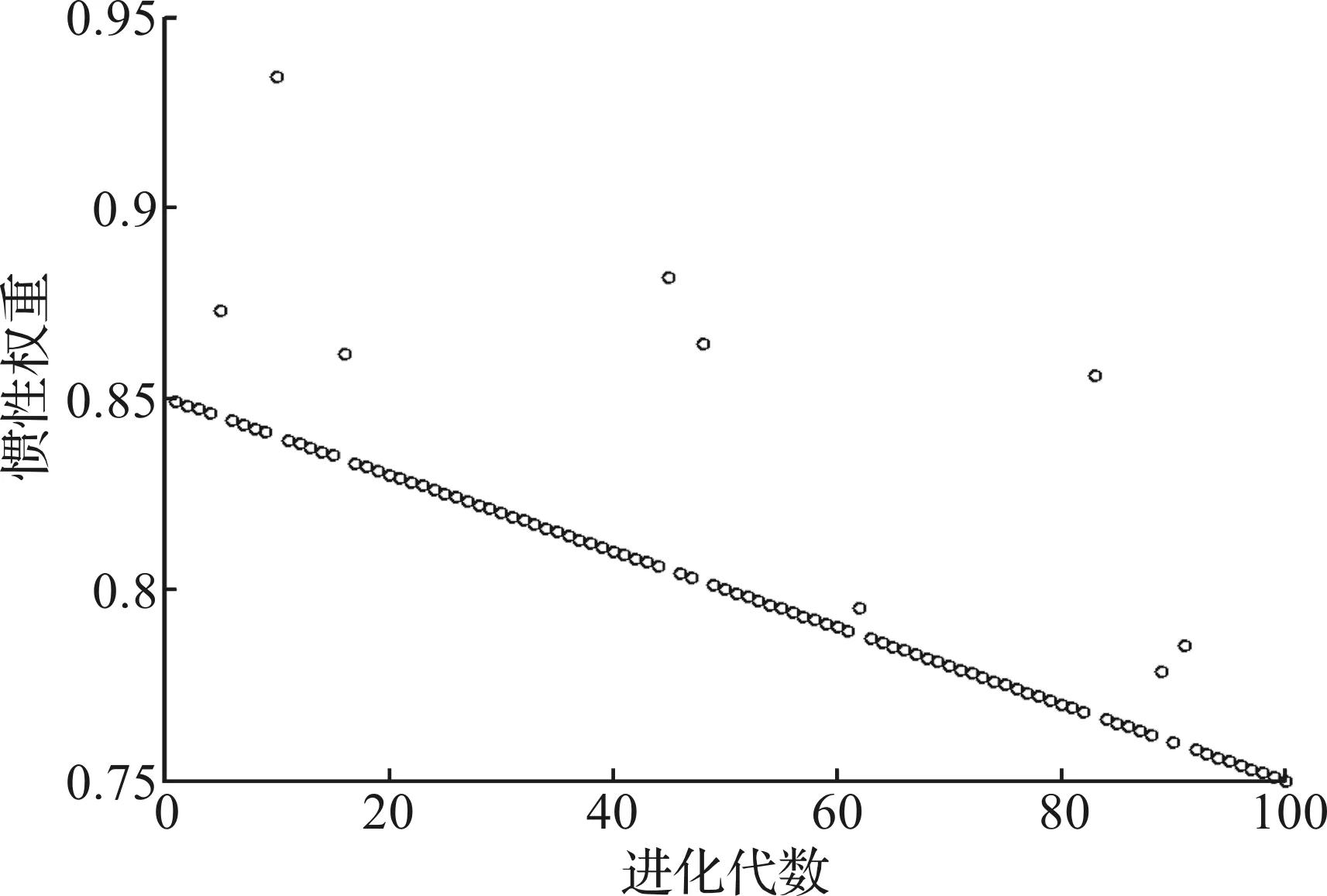
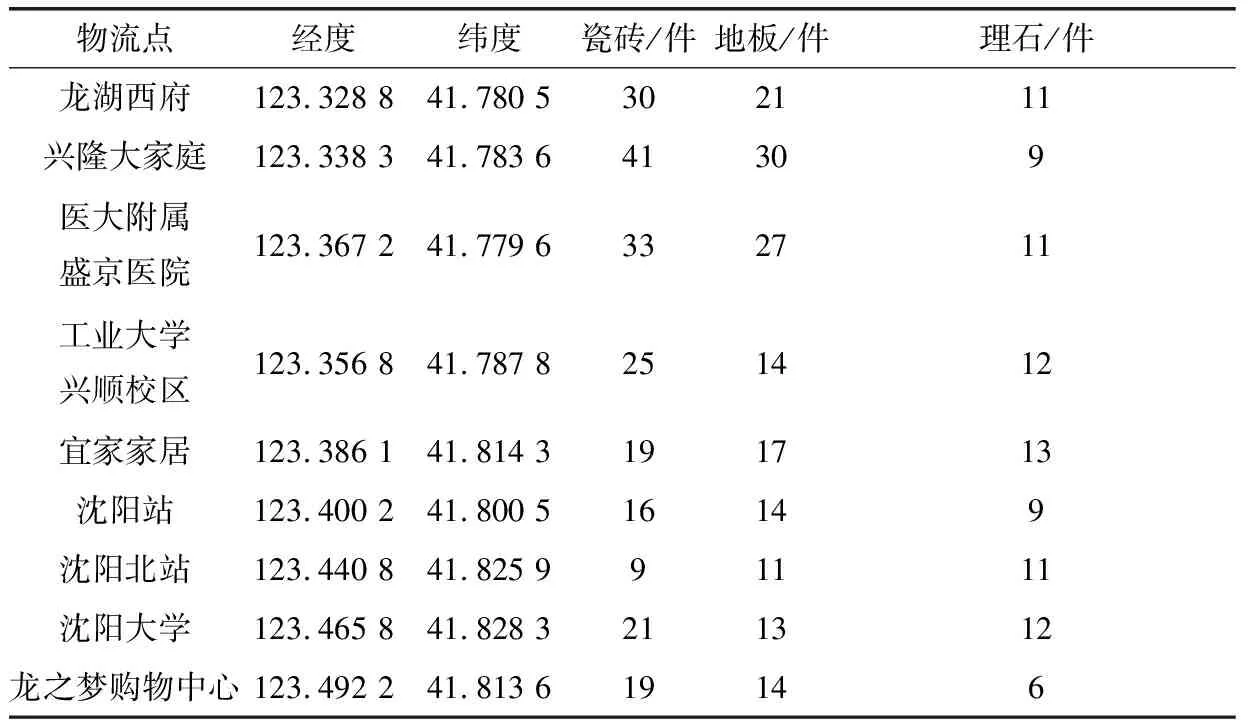
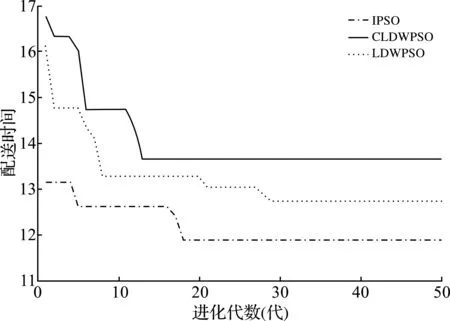
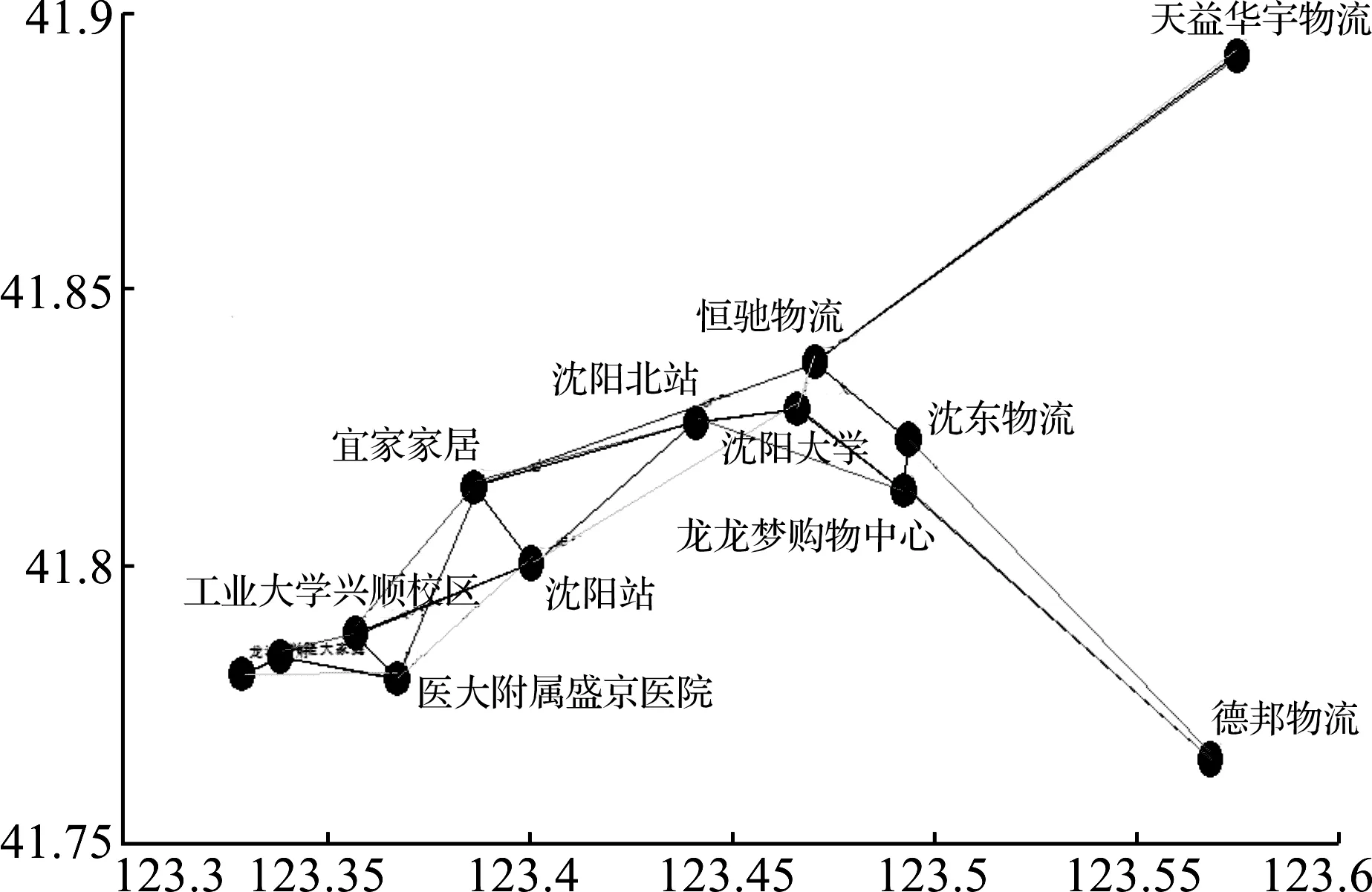
上式中用i=1,2,…,N表示粒子编号，用t表示粒子维度，用d表示迭代优化次数，用w表示权重因子，用c1和c2表示加速系数，且0

2.2 惯性权重因子线性递减的粒子群算法

基本粒子群算法非常容易局部收敛。其中，惯性权重因子ω线性递减的粒子群改进算法受到研究人员的广泛关注。惯性权重线性递减的粒子群算法更新迭代计算公式如下述公式(4)所述。

(4)

式中：ωk—惯性权重因子的递减斜率；

ωmax—初设的最大惯性权重因子。

惯性权重因子ω的设置既影响收敛速度，又关系寻优精度，因此ω在粒子群方法中至关重要。若惯性权重因子取值较大则能够改善收敛速度，有利于全局搜索，但同时也降低了解的精度；若惯性权重因子取值较小则有利于改善局部搜索，达到寻优精度要求，但同时也会以其收敛速度为代价，并且使粒子群算法局部收敛的概率随之增加。采用粒子群算法时，在迭代前期，收敛速度较为重要；在其迭代后期，寻优精度的重要性愈发明显。

在惯性权重因子线性递减(LDW)方法优化过程中，惯性权重因子ω与进化代数t呈现线性递减的关系[8]，其递减斜率为ωk。其惯性权重因子ω和进化代数t的线性递减关系曲线(见图1)[8]。

图1 惯性权重因子ω和进化代数t的关系曲线

2.3 惯性权重因子线性递减的粒子群增加混沌随机数扰动法

由上面论述可知，相对于常规基本粒子群方法，惯性权重因子线性递减(LDW)粒子群算法，可以兼顾收敛速度和寻优精度，具有更好的寻优效果。但是这种线性递减的惯性权重因子ω并不能反映粒子群方法的实际搜索过程，因为粒子群方法的实际搜索优化过程的是非线性的，所以采用线性递减的惯性权重因子ω并不能有效改善粒子群方法的优化效果[8]。因此，粒子群算法迭代过程中，如果算法长时间的得不到更好的全局极值，可以采用迅速加入混沌随机数扰动的方法，选取合适的扰动可以使得惯性权重因子ω迅速递增，有效确保粒子群方法全局收敛至最优值。

由此，惯性权重因子线性递减的粒子群增加混沌随机数扰动后的更新迭代计算公式如下述公式(5)所述。

(5)

式中，At为惯性权重的混沌扰动随机数，在一定的扰动概率下，At∈(0,0.1)，其余，At=0。混沌现象是非线性系统中一种普遍的现象，它的变化过程看似混乱，实际上其内在具有规律性，能够在一定范围之内，按照自身规律不重复地遍历所有状态。具体的惯性权重因子的混沌扰动随机数At的随机公式如式(6)所述。

At=0.1×rand2×sin(π×rand)

(6)

其增加混沌随机数扰动的惯性权重因子ω和进化代数t的关系曲线(见图2)。

图2 增加混沌随机数扰动的惯性权重因子ω和进化代数t的关系曲线

2.4 随机加速度系数的粒子群算法

为改善粒子算法的优化性能，一部分学者对c1和c2的取值进行了深入研究。其中，一些研究表明，对于较多的优化问题，相比于采用固定加速系数的粒子群算法，采用动态加速系数的粒子群算法具有更好的优化性能；与对称策略的粒子群算法相比，非对称策略的粒子群算法具有更好的优化性能[9-10]。由沈艳等的研究成果可知，一般来说，加速度系数取值c1和c2的取值范围在(0.5,2.5)区间[11]。基于上述研究成果，本文给出一种随机生成加速度系数的原则：每次粒子群算法的迭代计算，c1和c2都取不同的值，其令c1≠c2。具体的权重的加速度系数c1和c2的随机公式如式(7)所述。

csum=2×(0.5+2×rand)r=randc1=r×csumc2=(1-r)×csum

(7)

式(7)中：csum—c1和c2的和值;

r—为c1的比例系数；

1-r—c2的比例系数。

2.5 粒子改进算法

由上论述可知，粒子群优化方法虽然优化搜索能力极强，但在迭代优化后期，粒子群优化方法面临降低收敛速度，以及因陷入局部收敛而不易得到令人满意的最优解的问题。为具有更好的寻优效果，克服粒子群算法的不足，兼顾收敛速度和寻优精度的性能，本文提出了一种新的粒子群改进算法，该算法同时改进加速度系数和惯性权重，记为IPSO。具体的计算步骤如下所述：

Step 1初始化混合优化算法的各项参数：粒子种群规模(粒子数量)N、迭代次数d、最大惯性权重ωmax、惯性权重因子的递减斜率ωk；

Step 2随机生成N种不同的解，也即生成初始种群；

Step 3计算N个粒子的适应度函数值，并基于此对当前粒子群进行排序，以得到个体极值和全局极值；

Step 4采用公式(7)得到当前迭代次数下的加速度系数c1和c2；

Step 5采用惯性权重因子线性递减(LDW)的粒子群增加混沌随机数扰动法的更新规则对所有粒子进行更新；

Step 6确定迭代次数是否达到最大，如果达到最大则转步骤Step 7，否则转步骤Step 2；

Step 7输出计算得到的最优解的适应度函数值。

3 仿真实验

3.1 基于测试函数的仿真对比

基于3种不同的测试函数，采用粒子群改进算法(IPSO)、惯性权重因子线性递减(LDW)的粒子群增加混沌随机数扰动法(CLDWPSO)和普通的惯性权重因子线性递减粒子群算法(LDWPSO)求极小值，具体的仿真结果如下所述。

(2)De jong函数，最优解为0.0。其De jong函数的解析式为F(x1,x2)=100×(x1-x2)2+(1-x1)2。

具体的函数的寻优测试仿真结果(见图3—5)。

图3 采用Sphere函数的寻优测试仿真结果图

图4 采用Dejong函数的寻优测试仿真结果图

图5 采用Schaffer函数的寻优测试仿真结果图

由图3—5可知，粒子群改进算法(IPSO)的算法寻优能力最强，其寻优结果(见表1)。

表1 3种测试函数下的粒子群改进算法(IPSO)的仿真结果统计表

3.2 基于实际算例的仿真对比

对于一个物流运输中心配送路线优化问题的实际算例，分别采用粒子群改进算法(IPSO)、惯性权重线性递减(LDW)的粒子群增加混沌随机数扰动法(CLDWPSO)和普通的惯性权重线性递减粒子群算法(LDWPSO)求最优的配送路线，使得配送总成本和配送总时间都尽可能的小。该实际算例选取沈阳市区的基础建材配送案例，该案例中，含5辆配送车辆，车速均为15 km/h，配送成本50元/h分别可最多运送130件相关产品，不可混合运输。此外，实际算例有9个客户节点和4个物流中心。具体的相关数据(见表2—3)。

表2 物流中心相关数据表

具体的物流运输中心配送路线优化问题的寻优仿真结果(见6—7)。

表3 客户点相关数据表

图6中，粒子群改进算法(IPSO)最优。依据求解得到的配送路线进行配送，其配送时间总和为11.89 h，配送成本为594.5元。粒子群改进算法(IPSO)寻优得到的具体的配送路线优化结果(见图7)。图7中，红色和蓝色线条示意了运送瓷砖的2辆车的配送路线，黄色和绿色线条示意了运送地板的2辆车的配送路线，黑色线条示意了运送理石的1辆车的配送路线，其配送顺序和配送选择都是非常合理的。

图6 物流运输中心配送路线优化问题的寻优仿真测试结果图

图7 物流运输中心配送路线优化仿真结果图

4 结 论

本文提出了一种粒子群改进算法(IPSO)用于解决物流中心配送路径优化问题的优化模型。该方法一方面在惯性权重线性递减的基础上，加入了合理的混沌随机数扰动量；另一方面，每一次迭代计算，都采用随机的非对称的加速度系数c1和c2，从而使粒子群算法得到更加令人满意的最优解，进一步提升了粒子群算法的优化性能。最后，本文采用了Sphere函数、De jong测试函数、Schaffer测试函数和一个具体的物流中心配送路线优化问题的实际算例对本文提出的改进算法IPSO、增加混沌随机数扰动的惯性权重线性递减(LDW)的粒子群算法(CLDWPSO)和普通的惯性权重线性递减粒子群算法(LDWPSO)进行仿真测试，其仿真结果都能够表明本文提出的改进算法(IPSO)优于其它另外两种优化算法，具有更佳的寻优性能，更适合于物流中心配送路线优化问题的求解。