基于蒙特卡洛采样的橡胶复合材料内部导电网络建模研究

刘蔓霄，陶青川，赵凤媛

（四川大学电子信息学院，成都 610065）

0 引言

近年来随着人工智能的发展，智能穿戴让我们的生活越来越便利，这时好的传感器材料就显得尤为重要。由于导电橡胶在抗静电、电磁屏蔽、过流/过热保护、力敏和气敏良好等优点，近年成为国内外研究重点。导电橡胶材料的导电性能最终是由其所形成的导电网络所决定，因此，设计和构建有效的导电网络是改善材料导电性能的根本途径。由于近年来复合材料的更新，国内外少有人对橡胶材料的内部导电网络进行研究。本文根据前人对碳纳米管研究，围绕橡胶材料的逾渗阈值、惨杂物浓度和长径比对材料导电率影响为研究重点。研究过程基于三维空间，通过蒙特卡洛采样模拟出在以均匀排列天然橡胶胶乳球为基底、随机位置填充的碳纳米管为导电体的可穿戴传感器材料的内部导电网络，如图1（a）所示。由于胶乳球是不导电的，碳纳米管的导电网络构成了整个材料导电特性，如图1（b）所示。通过大量实验模拟材料内部网络的结构，建立导电网络结点方程，计算单位体积内材料的导电率模拟实体材料的导电率，从而分析材料的导电性能。

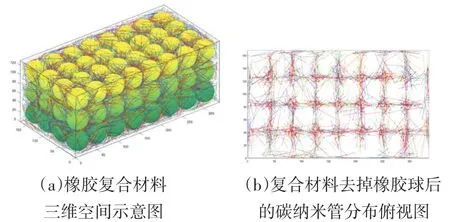
图1

1 导电网络的构建

不同于单根碳纳米管，柔性传感器材料的性质取决于分散于基体中的无数碳纳米管相互之间的作用。聚合物基底一般不导电，导电的碳纳米管随机分散，如果浓度过低，那么材料内部没有完整的导电通路。当碳纳米管的浓度达到一个阈值时，材料内部形成相互连通的导电网络，复合材料表现出导电性。与一般的碳纳米管复合材料相比，带橡胶球体的复合材料能够节约大量的碳纳米管材料，同时导电性能更好，形变的灵敏度也更好。

1. 1 渗流网络模型及隧道效应模型

导电橡胶材料内部的碳纳米管的分布与浓度决定了材料的导电性，研究整个导电网络的导电性的前提是了解碳纳米管的导电特性。碳纳米管与普通炭黑、金属颗粒不同，具有纳米级直径与较高的长径比。纳米级的导电填充物中微观粒子存在雷布罗意理论[1]中的波粒二象性。电掺杂物之间不是像渗流理论[2]描述那样，完全“接触”时才能形成导电网络。针对于纳米级的颗粒，由于范德华力的作用，颗粒间的间隙h与颗粒尺寸相当时，颗粒之间的连接存在隧道效应的作用。Simmons[3]等人计算出颗粒间的隧道效应电导可以表示为：

∂0是颗粒间间隙最小时的电导率，x是隧穿概率最小距离，在1nm级，h是颗粒间的距离。由上式可以看出当颗粒尺寸很大时，颗粒位置的稍微变化都会让电导率发生很大变化，而且只有当颗粒紧密接触网络才是导通的。当颗粒直径D接近于nm级时，在一定连通网络的颗粒浓度下，增加颗粒的浓度并不会较大改变接入网络的颗粒数，而是会影响颗粒间的间隙。Balberg[4]对纳米级颗粒与的渗流模型做了具体分析，结果表示纳米级的Ni导电粒子在不考虑隧穿效应时仿真曲线与实验结果偏差太大，当考虑隧穿效应时仿真曲线与实验结果比较相符。在王志峰[5]、唐力[6]等人的研究中可以看出碳纳米管之间的导电特性也应该考虑隧道效应，而且当碳纳米管电导率>10^4S/m时隧道效应引起的电阻还在网络中可能占主导地位。

从前面的分析可以知道，碳纳米管导电网络的实际电阻由两部分组成：①连接在通路中的碳纳米管的本征电阻Rd；②由隧道效应引起的碳纳米管之间的有效间隙的结电阻Rg。

本征电阻Rd可以表示为：

L表示接入到电路中的有效碳纳米 管长度，δCNT表示碳纳米管的本征电导率，D表示碳纳米管直径。对于结电阻，我们选取硬核模型的碳纳米管为研究对象。当CNT之间的接触距离大于0小于隧穿截止距离hcutoff时，此时两管之间电子隧穿效应，有电流流过，可以导电，此时结电阻为Rg。根据Simmons[3]等人的研究结果，碳纳米管结电阻可以如下表示：

其中，U是结电势差，A是隧道截面积可用碳纳米管直径D的平方代替，J是隧道电流密度，P是普朗克常数，h是两根碳纳米管的间距（中心轴线距离），e是电子电荷，m是电子质量，P是普朗克常数，λ是势垒高度。

1. 2 碳纳米管微观网络建模

如图2（a）所示，我们选择带有半球形帽的实心圆柱来模拟硬核碳纳米管，圆柱外面包裹一层厚度为的隧道效应有效作用区。碳纳米管生成随机坐标A(Ax,Ay,Az)作为一条CNT的起点，然后生成随机单位向量，根据式（4）可以得到终点坐标B(Bx,By,Bz)。通过上诉CNT产生过程，基本的导电网络结构模型就有了，如图1（b）所示。接下来我们便要根据模型与预先设定的hcutoff，建立每根CNT之间的关系，从而计算网络导电率。

图2

以上的工作已经建立了内部CNT的相互关系，但是我们的目标是要计算单位体积网络的电阻值。接下来我们就要计算完整的导电网络，首先将未经筛选的整个网络转换成无向图。基于图像的连通域寻找算法的启发，我们选择了基于图论的宽度优先遍历（BFS）算法。相对于文献[6]的迪杰斯特拉算法，选择此算法的原因主要有以下两点：①宽度优先遍历基于队列的实现模式，时间复杂度为O（n），可以节约大量的计算时间。算法示意图如图3。②我们后期用节点电压法计算网络电阻值时可以把那些在网络中支路但电流为0的CNT纳入计算，并不会影响最后计算结果。如图3中红色部分CNT，虽然在网络中，但是支路电流为0。

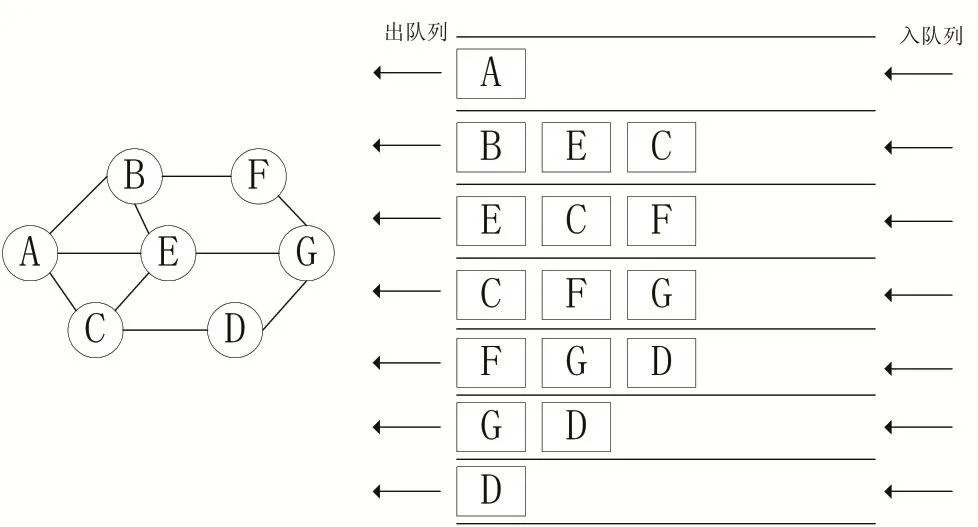
图3 BFS算法示意图

2 网络电路通路解算

上节已经介绍了获取导电网络的建模步骤，下面将具体针对复合材料内部导电网络进行数值分析。对碳纳米管导电网络进行数值计算过程中，首先需要将碳纳米管网络等效成纯电阻网络，然后再对纯电阻网络求解其等效电阻和电导率。

2. 1 节点电压分析法

节点电压法实质是基于基尔霍夫电流定律。基尔霍夫电流定律是指对任意电路中的节点而言，所有流入该节点的电流的总和等于所有流出这个节点的电流的总和。假设进入某个节点的电流为正值，离开这个节点的电流为负值，则所有涉及这节点的电流的代数和等于零。通常我们选取一个节点为参考节点（作为0电势点），其余n-1个节点到此节点的电压为ui。

在RVE空间导电网络中选取一小部分参与导电的碳纳米管进行分析。经过转化后形成的等效电阻如图4所示，其中Rd表示接入网络中碳纳米管的本征电阻，Rg表示的是两根碳纳米管之间的结电阻，其电阻值得计算方法在上一节中已经具体讨论。

2. 2 建立网络节点方程

有了建立方程组的理论基础，我们接下来讨论怎么建立方程组。在我们研究模型中通常参与导电的CNT有上百根，按照节点电压法节点数也会很多。首先我们需要找出所有的节点才能建立节点方程。我们需要根据结电阻与本征电阻建立起网络的节点方程。如图5所示，红色圆圈表示需要建立的节点，通过节点来表示本征电阻与结电阻之间的串并联关系。

图4 导电网络向电阻计算的转化过程

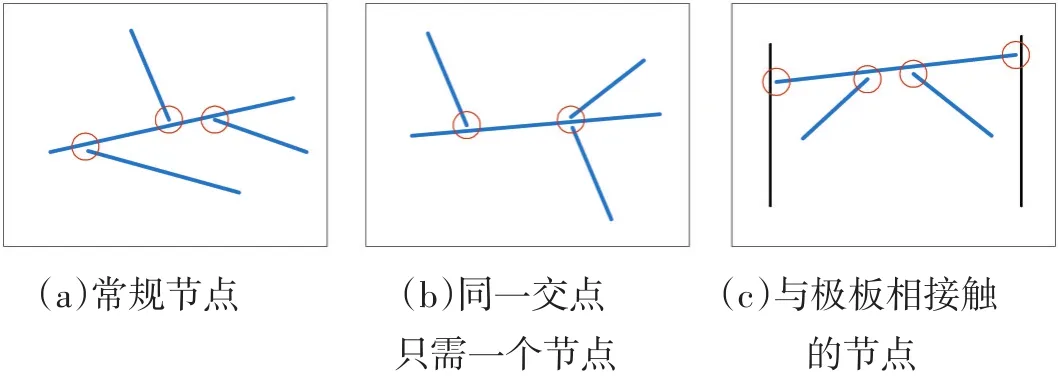
图5

根据上面步骤可以标记所有的节点，根据基尔霍夫定律第一定律和欧姆定律，通过节点n的电流可以表示为：

我们假设网络中与左极板相接触的所有节点作为一个初始节点（n=1），电流I1为1A。与右极板相接触的所有节点作为一个末节点（n=k），电流I1为-1A。导电网络内部流过其余节点的总电流恒为0。设节点1的电势为0，则节点n的电势为un。根据节点电压法和上式可以构造导电网络内各节点的电流、电压与电导的关系方程组如下式：

gkn为节点k和n之间的电导，表示与节点k相连的所有电导之和。由于复合材料中只有导电惨杂物的浓度达到一定时，才会有完整的网络形成，所以一般k值会比较大，对计算方程的解造成困难。我们把没有互相连接的节点看成电阻无穷大，故而电导记为0，这样我们的方程组中将会有大量的0形成稀疏矩阵，方便了我们的计算。

根据欧姆定律，碳纳米管导电网络的等效电阻在数值上等于左极板和右极板之间的电势差与流过他们的电流之比。假设输入电流为1A，所以根据方程式（7）可以计算出等效电阻，那么导电网络电阻率为：

其中L是基底材料沿着导电方向的长度，也就是两极板之间的距离，S为垂直于导电方向的网络空间的截面积，也就是基底的宽×高。

3 实验结果与分析

建立了导电网络模型，我们就要开始用模型去验证开始的假设是否合理。首先导电网络的导电性主要取决于网络中碳纳米管的本征电阻与隧道效应引起的段电阻。在王志峰[5]等人的研究中发现当导电率ρ>104S/m时，结电阻起主导作用。这时我们首先得确定网络的hcutoff（为了方便后面用HC代替），然后研究结电阻与本征电阻对导电网络的贡献。其次碳纳米管的长径比、浓度都影响着网络的导电率，之后也需要一一讨论。

3. 1 Hc值的讨论

由第二节的讨论我们知道最大隧道效应作用间隙HC不仅与碳纳米管的功函数e、聚合物介电常数等有关，还与碳纳米管的直径、长径比、浓度等有很大的关系。同时HC又可以通过设置模型中不同的H来得到。

由图6（a）可知在长1um、长径比100的碳纳米管在浓度为1.1%与0.9%的情况下，材料的的导电率随着H的增大而减少然后趋于稳定。浓度1.1%情况下，基本上在H=4左右，材料的导电率保持不变。浓度0.9%情况下，基本上在H=4.5左右，材料的导电率保持不变。说明浓度越大，HC越小。本文和对比文献中的研究结果趋势相同，但由于本文有橡胶球为基底，所以CNT的浓度在更低时便表现出了好的导电率，相对于文献中的材料需要的惨杂物更少，节约了成本。

3. 2 本征电阻与结电阻的分布规律

由于网络中主要是有结电阻与本征电阻组成，要讨论网络的导电性需要讨论结电阻与本征电阻对网络的贡献。当我们只考虑结电阻时，本征电阻的CNT段看成是通路电阻为0。只考虑本征电阻时，在小于HC时的间隙看成是通路，结电阻为0。为了方便计算，定义结电阻与本征电阻对网络的贡献分别为Φ（Rg）、Φ（Rd），计算方式如下：

由图7可见，在大于一定的CNT电导率下，结电阻的贡献远远大于本征电阻。说明选定惨杂物比例时，可以确定是否需要计算本征电阻。本文的模拟计算中选择的CNT电导率为10^4S/m，所以可以忽略掉本征电阻的贡献。

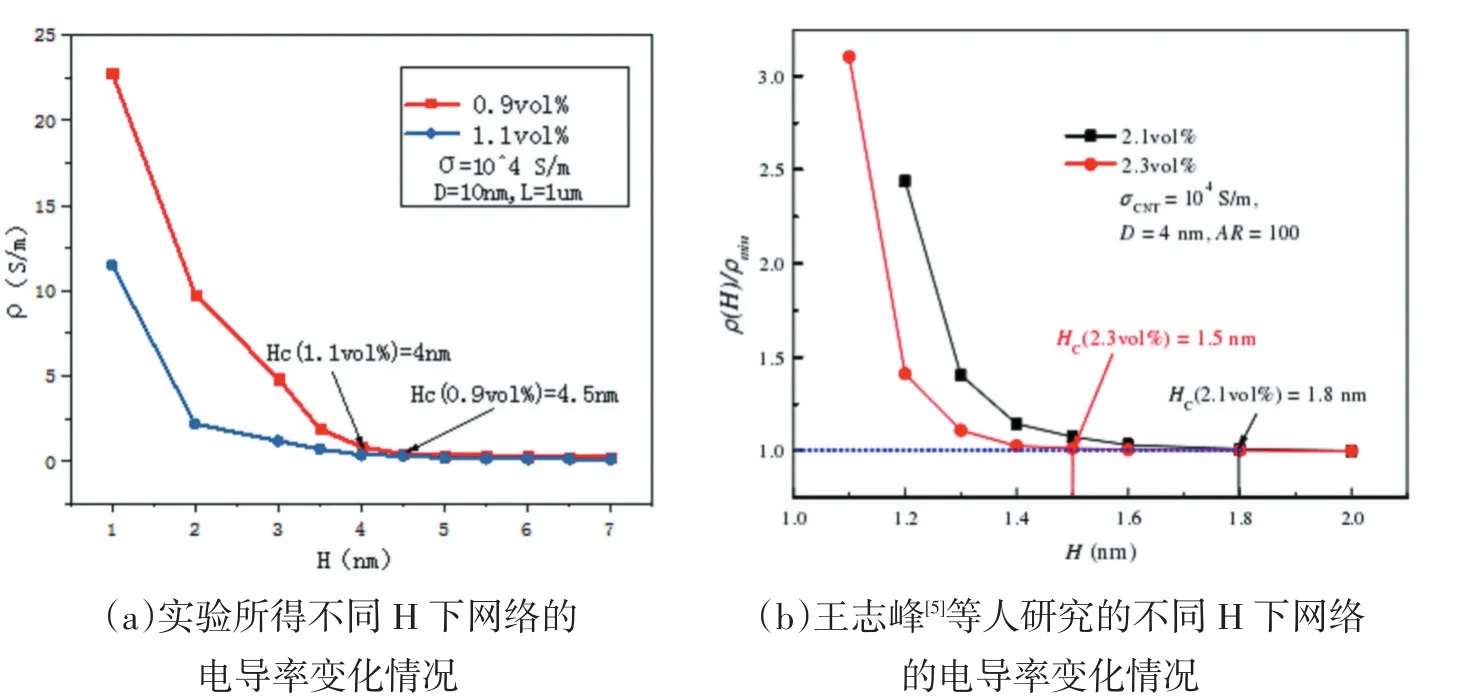
图6

图7

3. 3 长径比与对微观网络影响

根据 Kirkpatrick[1]、Compton[2]的讨论可知，复合材料的导电网络兼有渗流效应与隧道效应的特点。网络中的CNT长径比、直径、浓度等相关参数对网络的导电性都有影响。模拟中设置基底为2.1um×2.1um×2.1um的立方体，含有8个直径为1um的橡胶球，CNT浓度如表1的研究模型。研究了在CNT直径为10nm情况下，不同浓度与不同长度下网络的电导率。

由表1可以看出，在长径不变的情况下随着浓度的增加，电导率增加。在浓度不变的情况下随着长径比的增加，电导率增加。这和我们在上文中的讨论与文献[5-6]中的研究结果是一致的，同时结果也符合理论模型。

4 结语

本文基于前人在碳纳米管复合材料网络结构的研究基础上，研究了以橡胶球为基底的碳纳米管复合材料的内部网络结构。在MATLAB 2015b平台上建立仿真模型，研究了橡胶球为基底的碳纳米管复合材料的内部网络结构、隧道效应距离HC、CNT浓度和长径比等对导电网络的影响。结果表明，仿真模型符合理论原理与实际材料的导电特性。