DARPA2潜艇模型非定常流动粘性流场和水动力计算
2019-05-16于向阳姚凌虹孟庆昌刘巨斌张志宏
于向阳,姚凌虹,孟庆昌,刘巨斌,张志宏
(1. 海军航空大学青岛校区,山东 青岛 266000;2. 海军工程大学,湖北 武汉 430033)
0 引 言
潜艇水下操纵性能研究,与潜艇的安全航行密切相关,是其进行战术机动的重要保证,同时有着直接的作战应用背景。实际航行中的潜艇是一种复杂运动的组合体。一方面,其高速、大攻角及强机动的运动特征,使其呈现出非定常性与强非线性;另一方面,潜艇作有攻角机动时,即使攻角保持不变,由于边界层分离产生漩涡,流动仍然会呈现出非定常特征。这就给理论和试验研究带来了很大的困难,采用数值模拟是切实可行的研究方法[1–3]。
本文以DARPA2潜艇模型为研究对象,采用基于非结构化网格的有限体积法,数值求解非定常、不可压缩的RANS方程,湍流模型采用SA模式,在SA模式中,速度-压力耦合SIMPLE方法处理,对流项采用2阶迎风格式,非定常项采用2阶精度离散,隐式迭代求解方程组,非稳态迭代时间步长=2.322 4×10–3s(无量纲时间步长=3.73×10–2),步进200歩,非稳态流场速度由UDF给定,得到非定常粘性流场和水动力数值计算结果,并与文献[1]的实验结果进行对比。
1 数值离散方法
采用CFD软件数值求解DARPA2潜艇模型粘性流场和水动力,采用基于非结构化网格的有限体积法,数值求解非定常、不可压缩的RANS方程。
湍流模型采用SA模式,在SA模式中,生成项所采用的形式为:
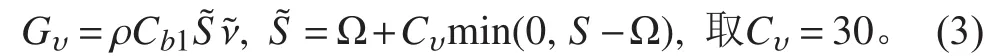
速度-压力耦合采用SIMPLE方法处理,对流项采用2阶迎风格式,非定常项采用2阶精度离散,隐式迭代求解方程组。计算雷诺数Re=5.52×106,初值收敛准则为所有求解变量的无量纲残差下降4个量级,非稳态迭代时间步长=2.322 4×10–3s(无量纲时间步长=3.73×10–2),步进200歩,模型的运动状态由UDF定义。
1.1 计算模型
计算对象为DARPA2潜艇模型(见图1),模型主要参数如表1所示,包括艇主体、指挥台围壳、尾附体。数值计算在惯性坐标系中进行,采用直角坐标系,原点取在模型头部顶端,x轴与艇体的对称轴重合,方向与无攻角时来流方向一致,z轴竖直向上,y轴水平,计算时直角坐标系保持为模型处于零攻角时的位置,当模型作操纵运动时,坐标不变,而模型与坐标系产生相对运动;在所定义的坐标系下, 规定来流的z方向速度分量正时为正攻角,初始攻角为0°。

图 1 全附体DARPA2模型Fig. 1 DARPA2 submarine model with sail and stern appendages mounted

表 1 DARPA2潜艇模型主要参数Tab. 1 DARPA2 model scale
考虑到模型本身的对称性,同时操纵运动仅为xz面内的非定常回转运动,在不影响数值计算的准确性前提下,仅对半艇体流动进行数值计算,以减少计算量;计算域为半圆柱体区域,范围:–2.0≤x/L≤5.2,–2≤z/L≤2,0≤y/L≤2,其中 L为艇体长度,L=2.236 m,计算域如图2所示。
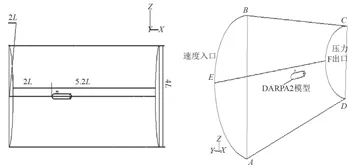
图 2 模型的边界条件设置Fig. 2 Boundary setting of the computational domain
1.2 边界条件
边界条件设置可分为初始流场状态和非稳态运动状态2个阶段。
初始边界条件(见图2):半圆柱体的左半圆面AEB(x/L=–2.0处)定义为速度入口,给定速度大小和方向;半圆柱体的右半圆面DFC(x/L=5.2处)定义为压力出口;半圆柱面的上、下两部分(EBCF/AEFD),及主体、指挥台围壳、尾附体,定义为无滑移壁面,速度分量和湍动能为0,以加速收敛,获得较好的初值;对称面上,法向速度分量为0,平行于对称面的速度分量的法向导数和所有标量的法向导数为0;初始攻角为0。
非稳态时模型作操纵运动,攻角发生改变,变化范围由0°~–25°,须调整边界条件,以适应运动状态的变化,此时定义半圆柱面的上半部分EBCF(z>0)为速度入口;半圆柱面的下半部分AEFD(z≤0)为压力出口,考虑到在迭代过程中,有可能存在数值上的反向流动,设置出口回流方向的方式为垂直于出口面;由于采用惯性坐标系,体网格是运动的,定义体网格和物面旋转中心(0.659 62,0,0)和旋转轴y轴,角速度由UDF定义。角速度曲线,具体描述如如图3及表2所示(实验数据来自文献[1])。
1.3 网格设置
体网格采用基于四面体的非结构化网格形式,边界层网格进行加密处理,网格密度由模型表面至远场由密到疏分布。
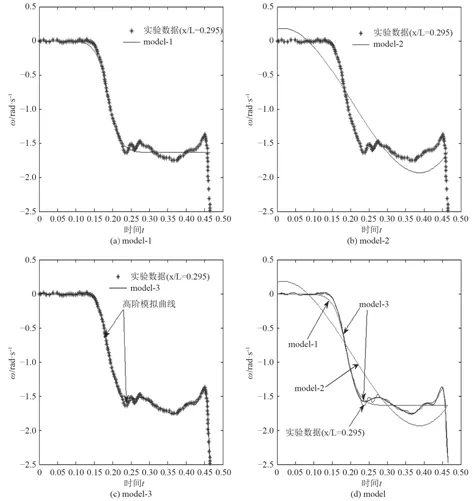
图 3 角速度ω随时间变化曲线Fig. 3 ω vs. time

表 2 不同模型的角速度函数Tab. 2 The function of ω for different model

表 3 网格主要参数Tab. 3 The grids for simulation
考虑到对模型进行非稳态运动模拟时,网格动态变化,网格需要均匀衔接,以避免网格的奇异变化导致迭代不收敛。
2 动态边界处理
本文中应用动网格技术处理含有动态边界问题的非稳态运动状态,边界运动由UDF定义。
2.1 UDF编写
用户自定义函数UDF(User-Defined Function)是CFD软件提供的一个用户接口,使用者可以通过它与CFD软件的内部数据进行交流,方便用户解决一些标准的CFD软件模块不能解决的问题[4–6]。
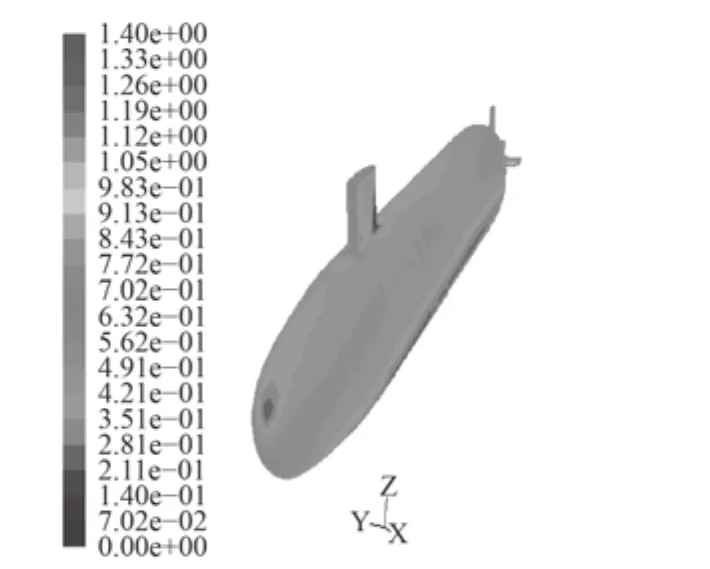
图 4 攻角–25°物面(model-1)Fig. 4 for the wall at –25° (model-1)

图 5 攻角–25°物面 (model-2)Fig. 5 for the wall at –25° (model-2)
本文考虑到非稳态问题的复杂性,以及计算机本身的运行环境(已安装Visual Studio C++ 开发软件),采用编译的UDF定义其运动(非稳态场的角速度函数),以提高执行速度[7]。
2.2 网格更新
动网格模型,即在每一个时间歩迭代之前,根据边界或物体的运动和变形来更新和重新构建计算域网格,从而达到求解非定常问题的目的[8–10]。而边界的形变和运动由UDF加以定义。计算中的网格更新情况如图6所示。

图 6 网格更新示意图(model-1)Fig. 6 The view of mesh motion (model-1)
由图6可知,艇体和附体的物面边界层都参与了网格的重构过程,网格质量没有受到影响,网格更新过程中没有负体积和大长宽比网格出现,从而保证了数值迭代的延续。
3 初始流场计算
为了得到较好的非定常结果,需要对初始流场进行讨论。本文中非定常因素,一方面,大攻角时,分离流动导致伴随涡的出现;另一方面,给定的模型运动状态,即角速度的定义本身就是随时间变化的函数。图7给出不同计算参数和边界条件下的初始流场变量收敛曲线。最初,分析初始时刻时,没有过多地考虑零攻角的流场特征,将边界条件半圆柱面的上、下两部分(EBCF/AEFD)分别定义为压力出口和速度出口,在迭代过程中流场变量波动起伏,近似周期性变化,但收敛精度未达到要求,如图7(a)所示;分析上述收敛精度持续不下的情况,可能是松弛因子过大的原因,将部分松弛因子降低30%,流场变量的波动情况消失,但收敛精度未出现改观,如图7(b)所示;观察到速度分量残差未发生变化,追溯根源,可能是边界条件有待优化,在图7(a)所定义的边界条件的基础上,将半圆柱面的上、下两部分(EBCF/AEFD)分别定义为无滑移壁面,速度分量残差迅速收敛,如图7(c)所示;图7(d)再次调整部分松弛因子,流场变量在925次迭代后达到收敛精度。
4 时间步长选取
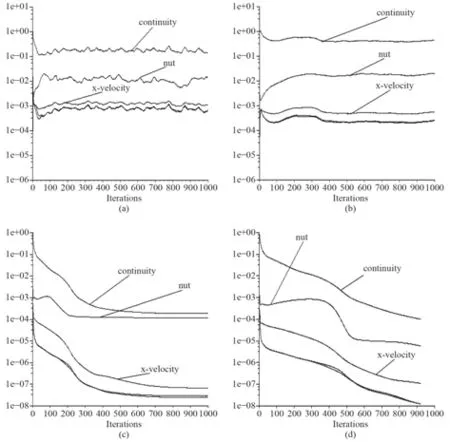
图 7 初始流场变量收敛历史Fig. 7 Convergence history of flowfied variables
初始流场由零攻角定常结果给出,进行非定常计算时需给定时间步长。依据文献[1]中的模型实验,给定角速度随无量纲时间t'的变化关系如图8所示,无量纲时间定义为,无量纲时间取值范围0~7.463 7时,对应的有量纲时间为0~0.464 48,计算时采用有量纲时间进行计算,非定常攻角范围0~–25°,考虑到时间步长对数值计算结果的影响,认为10–3s数量级已满足计算精度的要求。
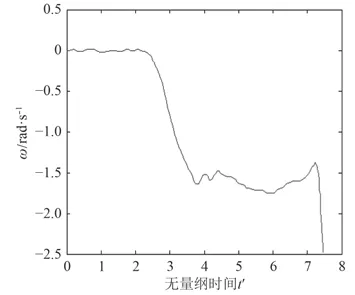
图 8 角速度ω(rad/s)随无量纲时间变化曲线Fig. 8 ω(rad/s) vs. non-dimensional time
5 计算结果分析
应用表2中的3种模型曲线,对模型运动进行定义。初始化流场后,进行非定常数值模拟。
为追求曲线拟合的精确性,采用最小二乘法高阶多项式拟合实验数据,如图3(model-3)所示,当n=18时,除波动较复杂的拐点处略有差别外,整条曲线基本重合;但进行非定常数值计算时,角速度给定值持续增加,在不到100歩的迭代过程中,迭代时间不到半数,残差竟迅速增至102数量级,超出预定值近100倍,最后导致计算结果发散。分析原因,认为是时间精度不够的原因,将时间步长下降一个量级后,结果仍旧如前所述。尝试时间步长的一味降低,势必导致计算量的增大。
重新分析计算结果发散的原因,非稳态问题本身需要进行空间和时间的离散,变量之间的耦合关系将导致非线性增强,同时高阶曲线拟合容易造成较大的截断误差,综合上述原因,应用model-2,降低多项式阶次拟合实验数据,以验证是否是截断误差过大导致结果发散;非定常结果稳定,且角速度按给定值正常迭代。
但model-2对实验数据拟合效果不够理想,需要寻找其他函数,进行数值计算。本例采用model-1对实验数据进行拟合,同时略去角速度变化较大的尾端,拟合效果较好,数值计算结果稳定。
5.1 水动力分析
图9给出了模型进行非定常数值计算时,升力系数CL随时间的变化情况。图中曲线unsteady,Quais-Steady+Time Lag和Quais-Steady为文献[1]中的实验结果,曲线unsteady为某一次非定常试验结果,Quais-Steady+Time Lag为20次非定常试验结果的平均值,Quais-Steady为准定常状态下的试验结果。

图 9 升力系数与时间的关系Fig. 9 Normal force development against time
从图中可以看到,定义相同的运动状态,unsteady的升力系数却表现出较强的不确定性,Quais-Steady+Time Lag曲线在描述unsteady曲线时符合程度也存在较大的偏差。分析上述问题产生的原因(参考图3),本文在对实验所定义的运动曲线的模拟上也存在局限性;同时,不得不指出非定常试验本身所具有的不确定性因素,如风洞中温度、风速的变化、及气流对操纵运动装置的影响(易使模型发生振动)等,随着时间的变化,流场中物理量的变化容易受到这些不确定因素的影响。
比较2种模型的数值计算结果,升力系数随时间变化平稳,在前0.25 s与实验值符合较好;模型model-1对升力系数的计算值在中间段(0.15~0.25 s)有较明显的减小过程(参考图3),这与model-1所定义的角速度曲线在中间段有一个负向加速过程相对应;模型model-2在初始阶段,升力系数由正转负,是与其所定义的角速度值在初始阶段大于0相一致的;要取得与实验一致的模拟效果,由实验中的不确定因素产生的误差需要加以考虑。
5.2 粘性流场分析
图10~图13给出了分别采用2种模型得到攻角–25°时物面压强系数和物面切应力系数的数值计算结果,两者在物面上的连贯性和均匀性均较好,在迎风处出现极值,这与理论上此处对应速度的最小值是相符合的。与定常攻角–25°(见图14和图15)时的结果相比,在变化趋势和数值分布上一致。
图16给出了攻角–25°时x/L=0.863截面速度向量图(model-1),在背风面可以清晰地看到有分离涡出现,反映了流场的粘性分离特性。
6 结 语
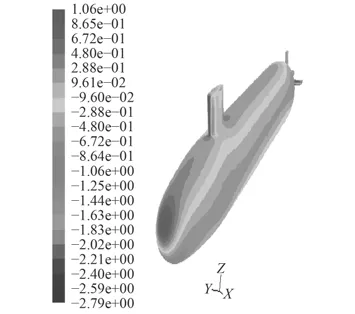
图 10 攻角–25°物面压强系数(mode-l)Fig. 10 Surface pressure cofficient at –25° (mode-2)

图 11 攻角–25°物面压强系数(mode-2)Fig. 11 Surface pressure cofficient at –25° (mode-1)
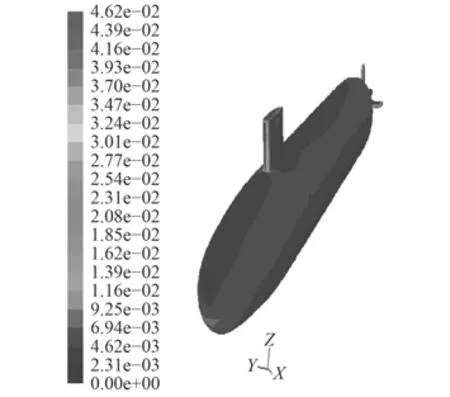
图 12 攻角–25°物面剪切力系数(mode-l)Fig. 12 Surface friction cofficient at –25° (mode-l)

图 13 攻角–25°物面剪切力系数(mode-2)Fig. 13 Surface friction cofficient at –25° (mode-2)
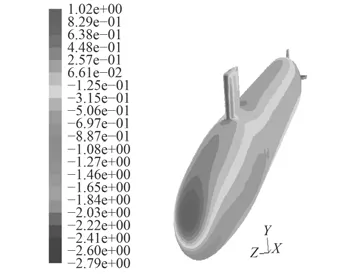
图 14 攻角–25°物面压强系数Fig. 14 Surface pressure cofficient at –25°
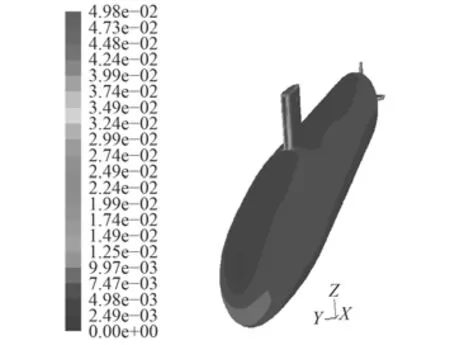
图 15 攻角–25°物面切应力系数Fig. 15 Surface friction cofficient at –25°
采用CFD软件数值求解非定常的DARPA2潜艇模型粘性流场和水动力,采用基于非结构化网格的有限体积法,数值求解非定常、不可压缩的RANS方程,湍流模型采用SA模式,在SA模式中,速度-压力耦合采用SIMPLE方法处理,对流项采用2阶迎风格式,非定常项采用2阶精度离散,隐式迭代求解方程组,非稳态迭代时间步长=2.322 4×10–3s(无量纲时间步长=3.73×10–2),步进200歩,非稳态流场速度由UDF给定。采用编译的UDF定义其运动(非稳态场的角速度函数)。
为了得到较好的非定常结果,需要对初始流场进行讨论。通过调整边界条件和部分松弛因子,初始流场变量在925次迭代后达到收敛精度。
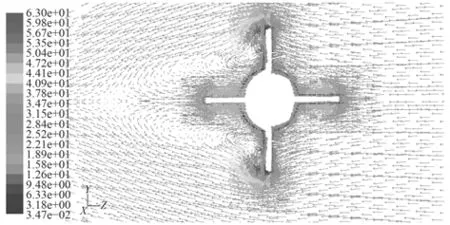
图 16 攻角–25°时x/L=0.863截面速度向量图Fig. 16 Velocity vector diagram at x/L=0.863 section and –25°angle of attack against time
在初始流场稳定的基础上,应用表2中的3种模型曲线,分别定义运动状态,进行非定常数值模拟。过分追求曲线拟合的精确性,采用高阶多项式拟合实验数据导致将计算结果发散;降低多项式阶次,得到稳定的非定常结果;采用model-1对实验数据进行拟合,拟合效果较好,数值计算结果稳定。
要取得与实验一致的模拟效果,由实验中的不确定因素产生的误差需要加以考虑。攻角–25°时物面压强系数和物面切应力系数的数值计算结果,在壁面上的连贯性和均匀性均较好,与定常攻角–25°时的结果在变化趋势和数值分布上一致。
