真空-堆载联合预压条件下复合地基固结解析解

(中原工学院 建筑工程学院，郑州 450007)

1 研究背景

真空-堆载联合预压法是真空预压和堆载预压共同加固处理软黏土地基的方法，是在真空预压法基础上发展而来的。该法因具有施工简便、固结快、强度增长明显、加载速率高、加固工期短、无环境污染等特点而被应用于工程实践[1-2]。大量研究表明[1,3-6]，真空预压和堆载预压的加固地基效果是可以叠加的，能够满足一些建(构)筑物对地基承载力和工后沉降的较高要求。目前，真空-堆载联合预压软黏土地基的施工工艺、技术、加固机理和沉降计算已比较成熟和完善，但对于真空-堆载联合预压复合地基的研究还需加强。对于真空-堆载联合预压复合地基的研究，学者们已做了大量工作[2,7-9]，主要体现在：①砂井桩加固软基的技术研究；②真空联合堆载预压轻筒复合地基的基本理论、受力特点和技术的研究；③刚性桩或混凝土芯砂石桩复合地基加固方法和固结特性的研究。虽然关于真空-堆载联合预压法与复合地基法共同加固软基技术的研究已取得较大进步，但是这些研究主要涉及桩体刚度较大的复合地基，而对于散体材料桩复合地基固结理论的研究还不多见。因此，进行真空-堆载联合预压条件下散体材料桩复合地基固结解析解研究是非常必要的，对于促进真空-堆载联合预压理论和复合地基理论有一定意义。

本文针对复合地基固结问题，考虑真空荷载和堆载荷载的共同作用，推导出初始孔压均布条件下真空-堆载联合预压复合地基固结解析解和平均固结度计算式；通过算例计算，分析探讨了真空-堆载联合预压条件下复合地基的孔压变化规律和固结特点。

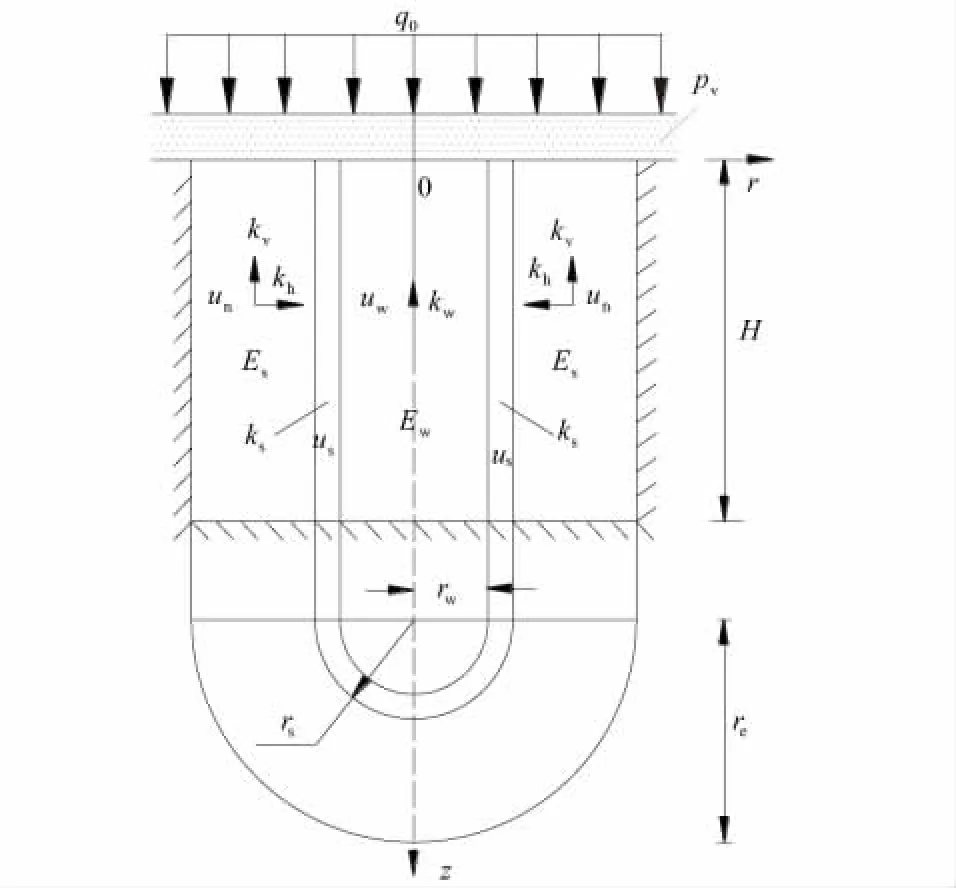
图1 计算简图Fig.1 Sketch of simplified calculation model

2 计算模型

2.1 计算简图与基本假定

图1为考虑荷载瞬时施加和初始孔压沿深度均匀分布的真空-堆载联合预压复合地基固结计算简图。其中，H为软黏土层厚度；kh，ks分别为地基土体未扰动区和扰动区的水平向渗透系数；kv为地基土体竖向渗透系数；kw为仅考虑桩体内竖向渗流时桩体渗透系数；Es，Ew分别为土体和桩体的压缩模量；rw，rs，re分别为散体材料桩桩体半径、土体扰动区半径和土体排水影响区半径；un，us，uw分别为土体未扰动区、扰动区和桩体内任一点的超静孔压；q0为一次瞬时施加的均布荷载；pv为一次瞬时施加的真空负压；r，z为径向及竖向坐标。设地基排水条件为PTIB，即顶部透水、底部不透水。

基本假定：

(1)土体是完全饱和的，土颗粒和水不可压缩，土体的变形完全由孔隙水的排出引起。

(2)等应变条件成立，即同一深度处地基土体和桩体的竖向变形相等。

(3)忽略桩体内的径向渗流；扰动区与未扰动区土体除径向渗透系数不同外，其它性质相同。

(4)土体、桩体的压缩模量和渗透系数保持不变。

(5)土体中水的渗流服从Darcy定律。

(6)任一深度z处，从土体中沿桩周流入桩体的水量等于桩体中向上水流的增量。

(7)堆载荷载一次瞬时施加引起的初始孔压沿深度方向均匀分布；真空负压荷载瞬时施加引起的孔压沿深度方向均匀分布。

2.2 固结基本方程和求解条件

对于复合地基，由力的平衡条件和等应变假定，可得出：

(1)

(2)

联立式(1)、式(2)得

Barron等应变条件基本固结方程为：

rw≤r≤rs，

(4)

rs≤r≤re，

(5)

其中，

连续条件为

(7)

边界条件为：

r=rw，us=uw；

(8)

(9)

(10)

(11)

(12)

初始条件为：

(13)

3 方程求解

参照Tang[10]和张玉国[11]关于散体材料桩复合地基固结方程的求解方法，利用式(4)—式(7)和边界条件，可以求出：

(14)

(16)

(17)

由式(16)、式(17)，可得

(18)

将式(18)代入式(3)，则有

(21)

(22)

考虑到采用上述求解条件，对式(21)—式(22)进行求解较为困难，因此，需要先对前面的边界条件进行齐次化变换，故令

(23)

根据式(18)、式(23)和初始条件式(13)，可得到新的初始条件，即

新的边界条件为：

(25)

(26)

同理，式(21)和式(22)可分别改写为

(27)

(28)

利用式(24)—式(26)，采用分离变量法，对式(27)和式(28)进行求解，可得：

(29)

(30)

根据式(29)和初始条件式(24)，利用三角函数正交性，可求得

因此，则有

(32)

(34)

(35)

同时，可以分别求得复合地基任一深度处的固结度和总平均固结度为：

(36)

不难发现，固结度计算式(36)、式(37)与文献[10]给出的荷载瞬时施加条件下初始孔压均布的复合地基固结度计算式在形式上完全相同，这表明正负压共同作用下的复合地基在固结时具有叠加效应。

(38)

另外，当桩体压缩模量取值为0且不考虑井阻情况时，即Y=0和kw→，式(34)和式(37)中的βm则变为

(39)

此时，式(34)和式(37)分别退化为文献[5]中考虑真空度不随深度变化和附加应力不随时间(深度)变化这一特殊情况的真空联合堆载预压竖井地基任一深度处孔压和地基固结度的解析解。

通过上述退化分析可知，真空-堆载联合预压条件下复合地基固结解的推导过程是正确和合理的。

4 计算分析

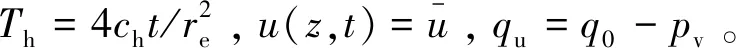
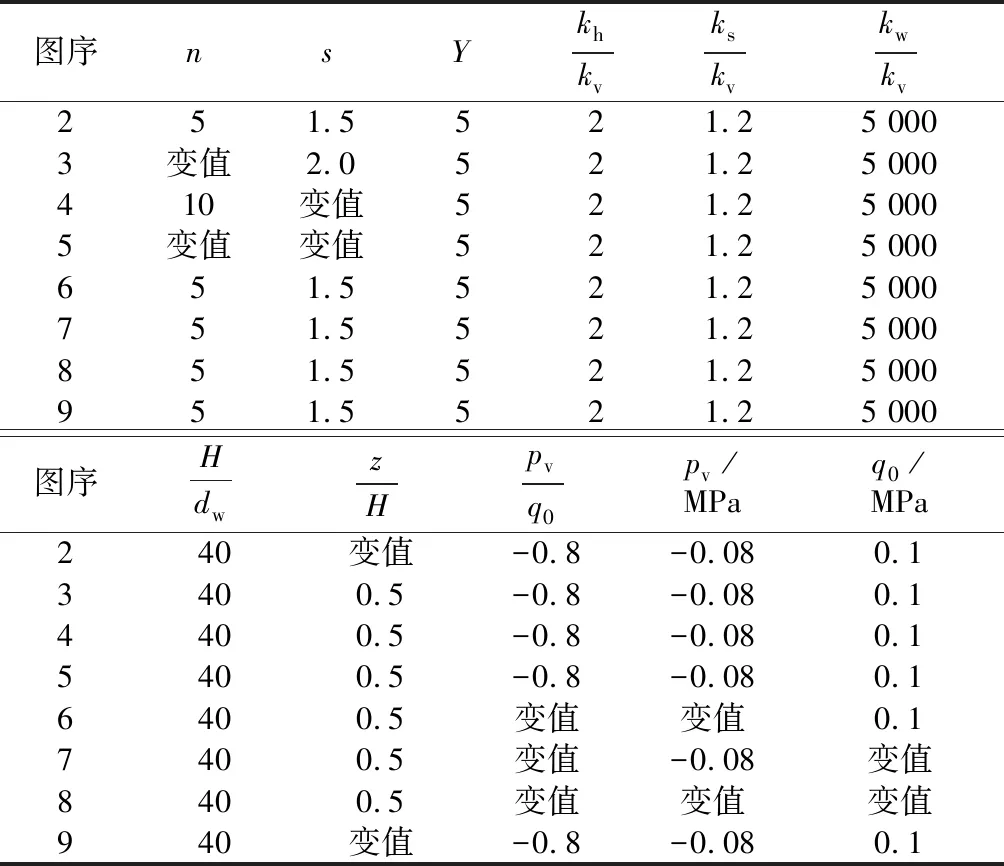
表1 计算参数取值一览表Table 1 Values of calculation parameters

图2为真空-堆载联合预压复合地基超静孔压在不同深度处随时间因子的变化曲线。分析可知，随着深度的增加，超静孔压不断增大，在地基浅部超静孔压随深度增加变化明显，在地基深部超静孔压随深度增加变化缓慢，这表明复合地基浅部土体固结快、深部土体固结慢。

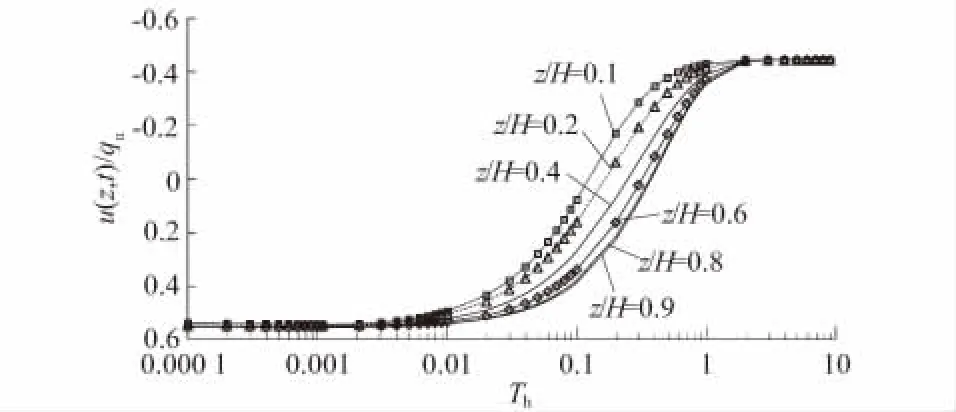
图2 z/H对超静孔压的影响曲线Fig.2 Influence ofz/Hon excess pore water pressure

图3—图5为桩径比n和扰动区大小s对复合地基超静孔压的影响曲线。可知n值和s值越大，超静孔压越大，即固结越慢。

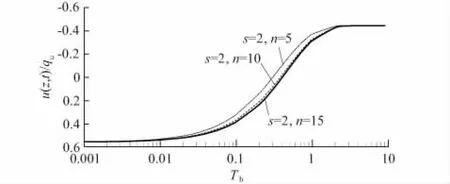
图3 桩径比n对超静孔压的影响曲线Fig.3 Influence ofnon excess pore water pressure

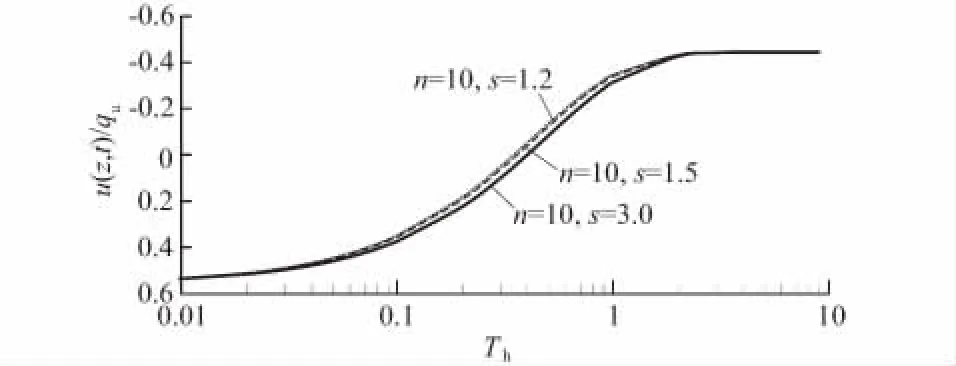
图4 扰动区大小s对超静孔压的影响曲线Fig.4 Influence ofson excess pore water pressure

图5 桩径比n和扰动区大小s对超静孔压的影响曲线Fig.5 Influences ofnandson excess pore waterpressure

图6—图8是真空荷载和堆载荷载对复合地基超静孔压的影响曲线。可知采用真空荷载或堆载荷载时，荷载越大，超静孔压越大；真空-堆载联合预压复合地基时，超静孔压是这2种荷载作用下产生的超静孔压的叠加；因此，真空-堆载联合预压复合地基固结时，固结具有一定的叠加效应。

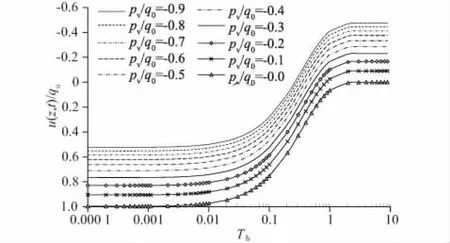
图6 真空荷载pv对超静孔压的影响曲线(q0=0.1 MPa)Fig.6 Influence ofpvon excess pore water pressure(q0=0.1 MPa)

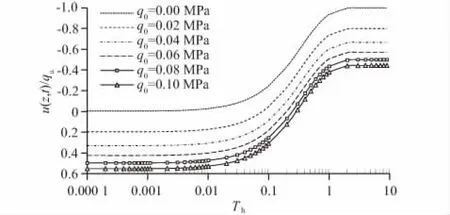
图7 堆载荷载q0对超静孔压的影响曲线(pv=-0.08 MPa)Fig.7 Influence ofq0on excess pore water pressure(pv=-0.08 MPa)

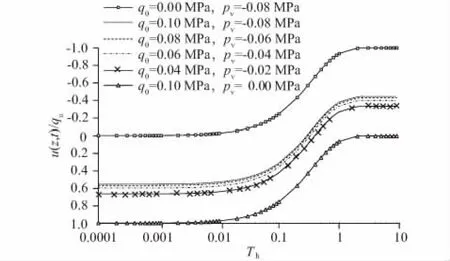
图8 真空荷载pv和堆载荷载q0对超静孔压的影响曲线Fig.8 Influence ofpvandq0on excess pore waterpressure

图9给出了不同Th值对超静孔压随深度变化的影响曲线。分析可知，当Th值一定时，超静孔压值随深度增加而增大，但超静孔压增加速度降低；在复合地基浅部，超静孔压随深度呈线性分布特征，但深度超过一定值时超静孔压呈非线性变化；同时，随着Th值增大，超静孔压沿深度方向的非线性分布特征越明显；Th值越大，超静孔压越小，超静孔压随深度变化也越小，这说明复合地基固结趋于稳定。

图9 Th对超静孔压的影响曲线Fig.9 Influence ofThon excess pore water pressure

5 结 论

(1)推导出真空-堆载联合预压复合地基固结问题的一般解；给出了真空-堆载联合预压复合地基任一深度处的固结度计算式和总平均固结度的计算式。

(2)堆载荷载一次瞬时施加和初始孔压均布的复合地基固结解是本文解的一个特例；在正负压共同作用下，复合地基在固结时具有叠加效应。

(3)桩径比n、扰动区大小s和加压方式均对复合地基固结有重要影响。n值、s值和荷载值越大，孔压越大，固结越慢。复合地基中，孔压值随深度增加而增大，但增加值逐渐变小，这表明地基浅部固结快、深部固结慢。

(4)时间因子Th值变化对复合地基孔压分布规律有重要影响。地基浅部的孔压呈线性分布；当地基深度超过一定值时，孔压呈非线性分布；当Th值越大时，孔压的非线性分布特征越明显。