山地光伏项目阵列间距计算方法研究

王春林，袁云，施俞安，高丹

(1.国电南京自动化股份有限公司，南京 210032；2.南京国电南自新能源工程技术有限公司，南京 210032)

0 引言

随着国家对光伏行业去补贴政策的持续推进，光伏上网电价逐渐降低，如何进一步降低光伏建设成本以推进光伏行业的发展是目前亟须解决的问题。我国山地丘陵地带较多，由于地势起伏较大，多数不适宜农业种植，土地利用价值相对较低，目前多以荒废的状态存在。若将此部分土地用于光伏建设，一方面可以降低光伏建设土地使用成本，另一方面可以提高山地丘陵地段的利用价值。

山地具有地形复杂多变的特点，显著的特征表现为坡度、坡向多变。由于坡度、坡向的影响，GB 50797—2012《光伏发电站设计规范》[1](以下简称GB 50797—2012)中的平地光伏阵列间距计算原理难以适用于山地光伏项目的阵列间距计算。现有相关文献对这方面的研究仅对东、南、西、北等特定坡向下不同坡度的光伏阵列间距计算方式进行研究[2-8]，或者仅对北、 东方向的坡度分量进行研究[9]，忽略了太阳方位角θ方向的坡度分量对光伏阵列间距的影响，建立的数学模型难以适用山地光伏项目不同坡向、坡度情况下的光伏阵列间距计算。本文结合山地的坡度、坡向特征信息，在平地光伏阵列间距数学模型基础上，对该模型进一步加以推导改进以适用于不同坡度、坡向的山地光伏项目的阵列间距计算。

1 光伏阵列计算

按照GB 50797—2012的要求，光伏方阵各排各列的布置间距应保证全年09:00—15:00(当地真太阳时)时段内前、后、左、右互不遮挡，即冬至日当天09:00—15:00时段内前、后、左、右互不遮挡。由于光伏阵列朝向为正南，对于平地光伏项目，光伏阵列各排在同一高度，因此不存在左右光伏阵列相互遮挡的情况。对于山地光伏项目，光伏阵列采用随坡就势的布置方式，也不存在左右相互遮挡的情况。因此只需计算出冬至日当天09:00—15:00时段内光伏阵列前后最大间距，即可保证全年内光伏阵列间互不遮挡。

1.1 平地光伏阵列间距计算

对于平地光伏阵列前后间距D的计算涉及当地纬度ø、太阳高度角α、转动角度αs、太阳方位角θ、太阳赤纬角δ、太阳时角ω、阵列倾斜面长度L、阵列倾角β等因素。

其中，太阳高度角

α=arcsin(sinø sinδ+cosø cosδcosω) 。

太阳方位角

θ=arcsin(cosδsinω/cosα) 。

阵列的竖直高度

h=Lsinβ。

阵列前后间距

D=Lcosβ+Lsinβcosθ/tanα。

其相互之间的几何关系如图1所示，数学几何模型如图2所示。

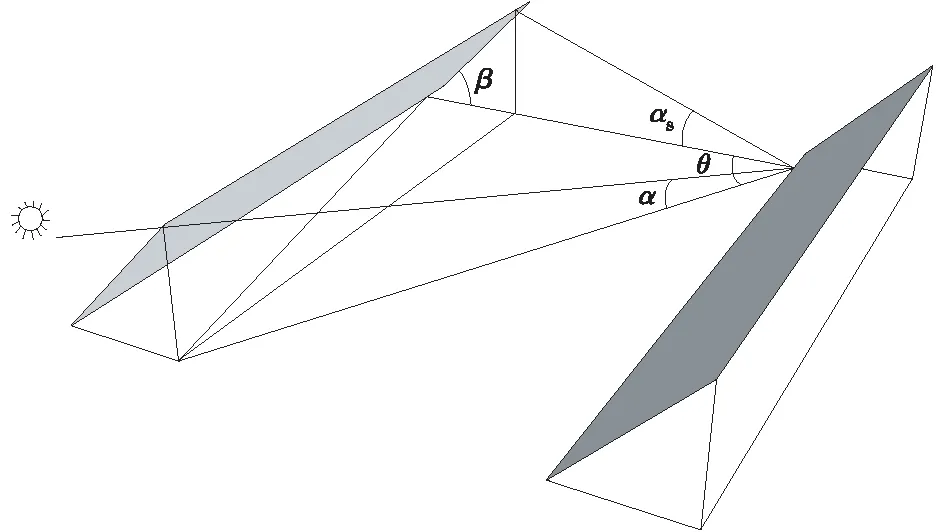
图1 太阳高度角α、方位角θ及光伏阵列之间的几何关系Fig.1 Solar elevation angle α, azimuth θ and geometric relationship between PV arrays

图2 平地光伏阵列间距计算数学几何模型Fig.2 Mathematical geometric model of plain PV array spacing calculation

1.2 山地光伏阵列间距计算

对于山地光伏项目，光伏阵列前后间距D的计算不仅涉及以上因素，还涉及地形特征因素坡度λ、坡向φ。本文以坡向为偏东坡(0<φ<π)随坡布置的光伏阵列间距为研究对象，根据日照规律，此时在全年真太阳时09:00—15:00时间段内影子最长的时间为冬至日15:00的时候，并且根据坡向分为以下3种情况进行详细分析。

(1)当θ+π/2≤φ≤π时，光伏阵列间距计算的数学几何模型如图3所示，根据图3a方位图，坡度λ分别在太阳方位角θ方向、E方向以及N方向上分别产生分量λ′，λ″，λ‴，此时λ′<0，表明在θ方向上表现为偏南坡，λ″<0，λ‴>0，坡向为东南坡，此时光伏阵列左视图、后视图数学几何模型如图3b、图3c所示。

由此得到

λ′=λcos(θ+π-φ)λcos(φ-θ) ，

λ″=λcos(π-φ)=-λcosφ，

λ‴=λsin(π-φ)=λsinφ。

阵列的竖直高度

h′= (Lsinβ-Lcosβtanλ″)/cosλ‴=

[Lsinβ+Lcosβtan(λcosφ)]/cos(λsinφ) 。

阵列前后间距

D=Lcosβ+h′[sinλ′+cosλ′/tan(α+λ′)]×

cosλ′cosθ=Lcosβ+{[Lsinβ+Lcosβ×

tan(λcosφ)]/cos(λsinφ)}{sin[λcos(φ-θ)]+

cos[λcos(φ-θ)]/tan[α+λcos(φ-θ)]}×

cos[λcos(φ-θ)]cosθ。

(2)当π/2≤φ≤θ+π/2时，此时光伏阵列间距计算的数学几何模型如图4所示。由图4a可知，此时λ′>0，表明在θ方向上表现为偏北坡，λ″<0，λ‴>0，坡向为东南坡，此时光伏阵列左视图、后视图如图4b、图4c所示。

由此得到

λ′=λcos(φ-θ) ，

λ″=λcos(π-φ)=-λcosφ，

λ‴=λsin(π-φ)=λsinφ。

阵列的竖直高度

h′= (Lsinβ-Lcosβtanλ‴)/cosλ‴=[Lsinβ+

Lcosβtan(λcosφ)]/cos(λcosφ) 。

阵列前后间距

D=Lcosβ+h′/tanα[cosλ′+sinλ′/

tan(α-λ′)]cosλ′cosθ=Lcosβ+

{[Lsinβ+Lcosβtan(λcosφ)/cos(λsinφ)]}/

tanα{cos[λcos(φ-θ)]+

sin[λcos(φ-θ)]/tan[α-λcos(φ-θ)]}×

cos[λcos(φ-θ)]cosθ。

(3)当0≤φ≤π/2时，此时光伏阵列间距计算的数学几何模型如图5所示。由图5a可知，此时λ′>0，表明在θ方向上表现为偏北坡，λ″>0，λ‴>0，坡向为东北坡，此时光伏阵列左视图、后视图如图5b、图5c所示。

图3 光伏阵列间距计算数学几何模型1Fig.3 Mathematical geometric model 1 of PV array spacing calculation

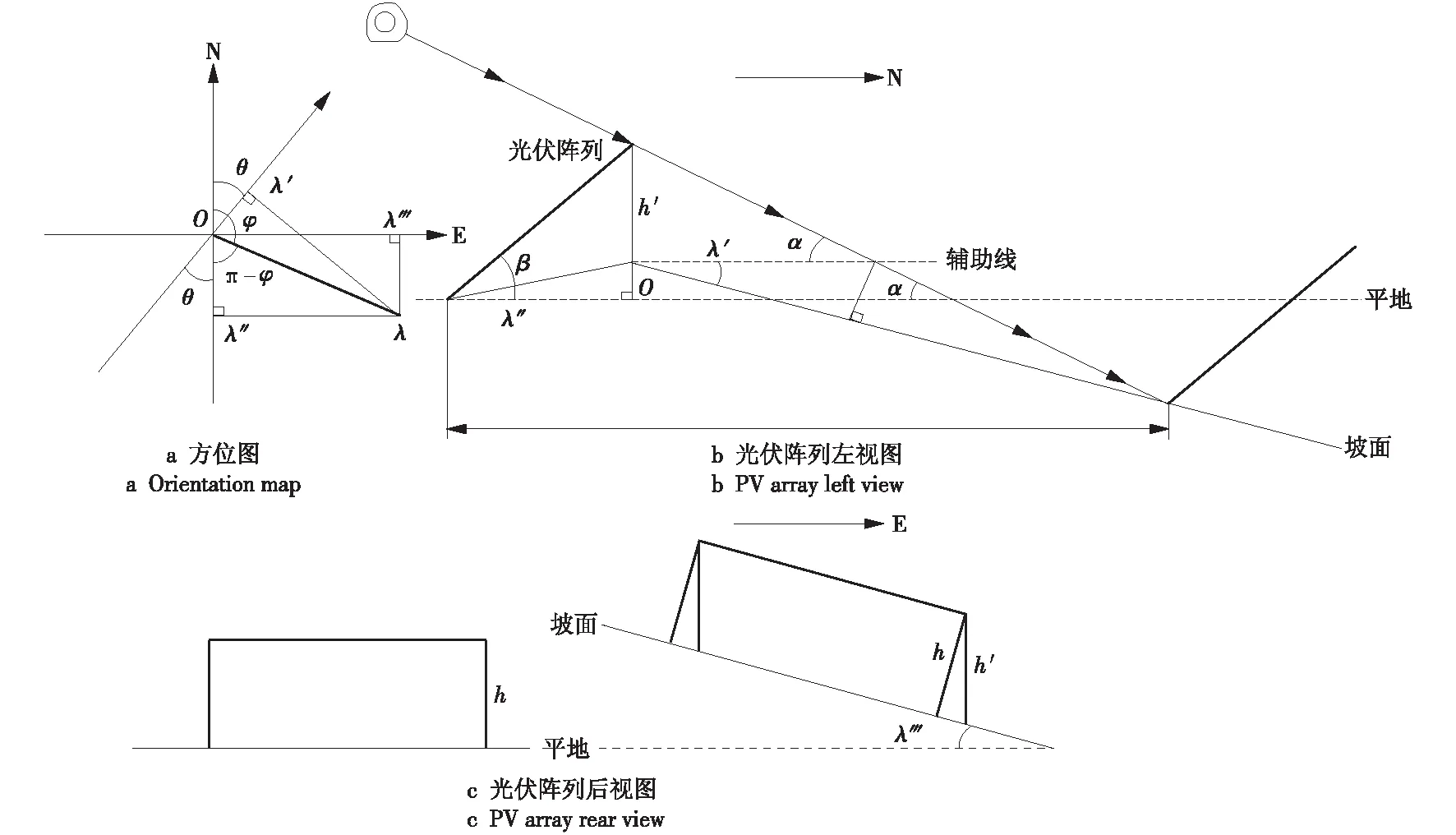
图4 光伏阵列间距计算数学几何模型2Fig.4 Mathematical geometric model 2 of PV array spacing calculation

由此得到

λ′=λcos(φ-θ) ，

λ″=λcosφ，

λ‴=λsinφ。

阵列的竖直高度

h′= (Lsinβ+Lcosβtanλ″)/cosλ‴=

[Lsinβ+Lcosβtan(λcosφ)]/cos(λsinφ) 。

阵列前后间距

D=Lcosβ+h′/tanα[cosλ′+sinλ′/tan(α-λ′)]×

cosλ′cosθ=Lcosβ+{[Lsinβ+Lcosβtan(λcosφ)/

cos(λsinφ)]}/tanα{cos[λcos(φ-θ)]+

sin[λcos(φ-θ)]/tan[α-λcos(φ-θ)]}×

cos[λcos(φ-θ)]cosθ。

从公式推导的结果可以看出，1.2章节中 (2) 和

图5 光伏阵列间距计算数学几何模型3Fig.5 Mathematical geometric model 3 of PV array spacing calculation

(3)给出的两种数学模型可以归到同一种类型，(2)和(3)主要不同之处在于h′的数学表达上。在(2)给出的模型中，λ″<0，λ‴>0时坡向为东南坡，在N方向上表现为南坡，而在(3)给出的模型中，λ″>0，λ‴>0时坡向为东北坡，在N方向上表现为北坡，通过角度的换算可以归到同一种数学模型中。

以上关于山地光伏阵列计算的数学模型是以偏东坡为例，由于日照规律以太阳时正午12:00时为对称轴呈现对称性，坡向为偏西坡的光伏阵列间距可以根据此对称轴转换为偏东坡，并根据以上数学模型计算出相应的光伏阵列间距。

2 案例应用分析

2.1 应用环境

某地区20 MW山地光伏电站项目，光伏场区占地面积较大，场内地形较为复杂，地势起伏不定，具体信息见表1。

2.2 光伏阵列间距计算

根据光伏阵列间距数学模型计算得到该地不同坡度、坡向的阵列间距，计算结果见表2，并由计算结果得到不同坡度条件下，光伏阵列间距随坡向变化的规律，如图6所示。

表1 项目基本信息Tab.1 Basic information of the project

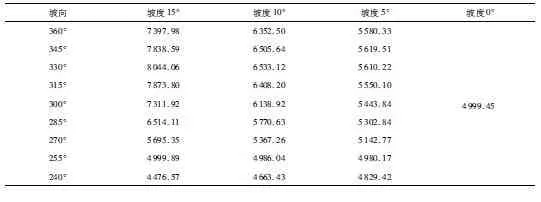
表2 不同坡度、坡向情况下的光伏阵列间距Tab.2 PV array spacing under different slopes and slop directions mm

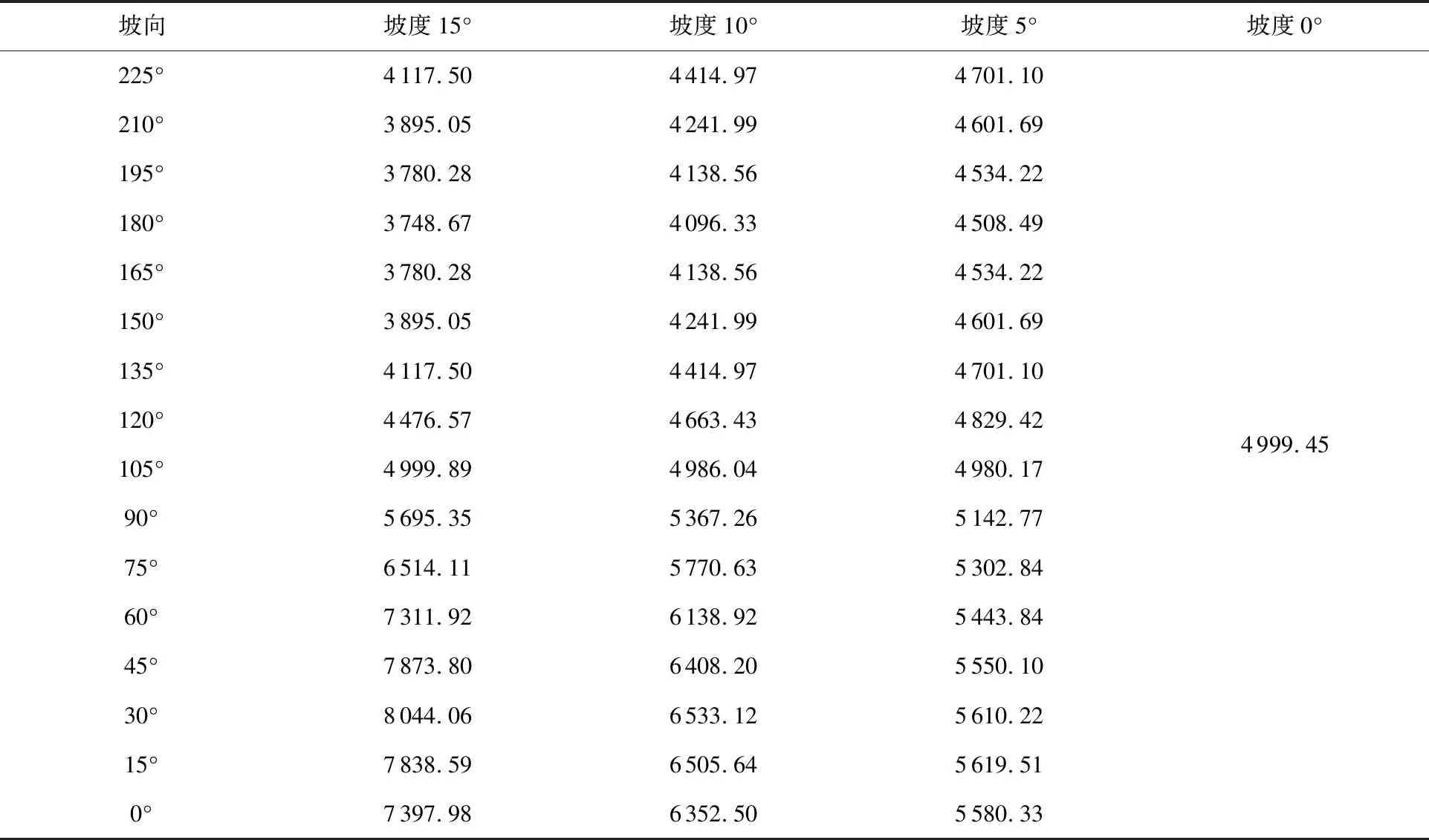
续表

图6 光伏阵列间距随坡向变化的规律Fig.6 The regularity of PV array spacing varying with slope direction

从表2可以看出，利用本文的光伏阵列间距计算模型可以快速得到不同坡度、不同坡向条件下的阵列间距，有利于全方位了解山地光伏项目区域内不同地形的光伏阵列间距，便于更精准地评估不同朝向地块的可利用性。

从图6中可以看出，不同坡度情况下，光伏阵列间距随坡向变化的规律基本一致，最小的阵列间距出现在坡向为180°的正南方向，但最大的阵列间距并不是出现在坡向为0°/360°的正北方向。根据阵列间距计算公式可知，阵列间距主要受纬度、阵列倾角、坡度3个因素影响，最大的阵列间距并不是出现在固定的坡向值上。

3 结论

本文通过研究山地坡度、坡向对光伏阵列间距的影响，建立相应的数学模型，最终得到一种能快速精确计算出不同坡度、坡向情形下的阵列间距的方法，并且通过该方法得到了不同坡度情况下，光伏阵列间距随坡向变化的规律。该方法能为今后的山地光伏项目前期选址及设计阶段经济性优化比选提供一种切实有效帮助。