基于前置反馈补偿的火箭靶弹解耦方法

刘 伟，魏志芳，曹红松

(1.中北大学机电工程学院，山西 太原，030051；2.重庆航天机电设计院，重庆 400039)

0 引言

由于旋转火箭靶弹在飞行过程中以一定的滚转角速度旋转，它独特的动态特性使其控制方法具有一定的特殊性，导致不能直接应用非旋转式战术导弹的现有研究成果，在技术层面提出了一些新的问题。火箭靶弹在飞行过程中以一定的滚转角速度旋转，其动态特性的独特性主要体现在俯仰和偏航通道之间的强耦合上，这些强耦合的主要原因包括Magnus效应引起的气动交联，陀螺效应引起的惯性交联以及运动学延迟诱导的控制交联。由于这些交联因素，旋转靶弹的运动学与控制模型可视为一个存在俯仰和偏航通道强耦合的双输入-双输出的动态系统[1]。针对双通道多输入多输出、强耦合、参数时变的特点，需要对靶弹的耦合特性和相应的解耦控制方法进行分析。

目前工程中经常使用基于插值的增益调度辅助解耦，由于需要预先计算大量的特征点，当特征点较少并且滚动导弹气动非线性较强时，基于插值法计算的反馈增益精度不高[2-4]。而一些非线性解耦算法，如动态逆解耦算法和H∞鲁棒变增益算法，需要的模型精度高，计算量大，比线性解耦算法更为复杂[5]。为了简化工程计算量，实现耦合矩阵的快速求解，本文提出了利用对角优势化特性设计动态预补偿矩阵的前置反馈补偿解耦方法。

1 前置反馈补偿技术

前置反馈补偿技术是采用一种动态预补偿矩阵来实现解耦的一种技术。通过引入一个预补偿器KP，使得KP·GP(s)是对角占优的，便可以将补偿后的俯仰、偏航通道进行单独设计，而不必考虑彼此的耦合作用[6]。前置反馈补偿解耦原理如图1所示。

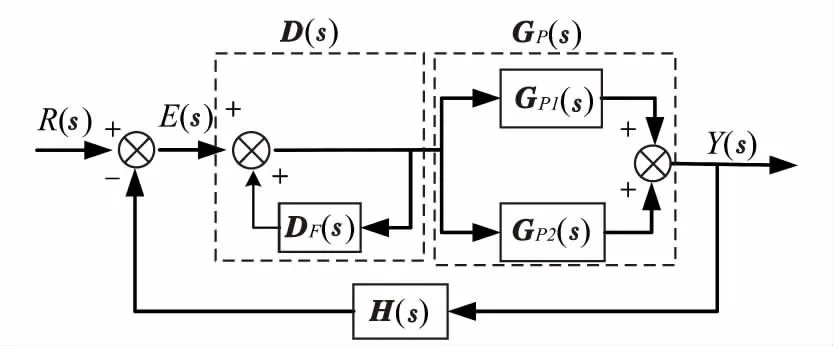
图1 旋转靶弹前置反馈补偿解耦原理图Fig.1 Decoupling principle diagram of pre-feedback compensation for target missile

图1中，R(s)，E(s)，Y(s)分别表示输入信号、偏差信号和输出信号、H(s)为反馈通道传递函数矩阵，GP(s)由代表主对角线元素矩阵的GP1(s)和代表非对角线元素矩阵的GP2(s)组成，表示耦合对象传递函数矩阵，D(s)表示引入的“预补偿器”矩阵。其完全解耦的补偿矩阵DF(s)为：

(1)

2 火箭靶弹解耦方法

火箭靶弹解耦方法是在靶弹运动学和控制频域模型基础上，将开环传递函数矩阵分解为动力学耦合和控制耦合，基于前置反馈补偿技术将补偿后的俯仰、偏航通道进行单独设计，进而实现靶弹姿态和过载解耦控制系统的设计。

2.1 运动学耦合特性分析

(2)

2.2 控制耦合特性分析

由文献[9]可知：

(3)

式(3)中，W(s)为控制耦合传递函数矩阵，W12和W21项表示由靶弹主体的旋转和转向装置延迟引起的交叉耦合，ωx为靶弹的滚转角速度，τ为舵机的一阶惯性常数。当ωx=0，W12=W21=0表明方向舵系统仅具有输入输出转换关系，没有耦合。当ωx≠0时，俯仰和偏航通道之间产生控制交叉作用，产生控制耦合。

2.3 火箭靶弹姿态解耦

2.3.1 控制耦合W(s)的解耦

由式(1)，式(2)得到W(s)的前置反馈补偿矩阵为：

(4)

2.3.2 运动学耦合G(s)的解耦

由于补偿解耦矩阵为前置反馈补偿矩阵，并设立在舵伺服系统之前，因此不能忽略控制耦合传递函数矩阵W(s)对反馈量的影响，因此由式(1)，式(2)，式(3)得到运动学耦合G(s)的前置反馈补偿解耦矩阵为：

(5)

结合式(1)—式(5)用结构图的方式表示俯仰和偏航通道姿态控制系统的前置反馈解耦，如图2所示。

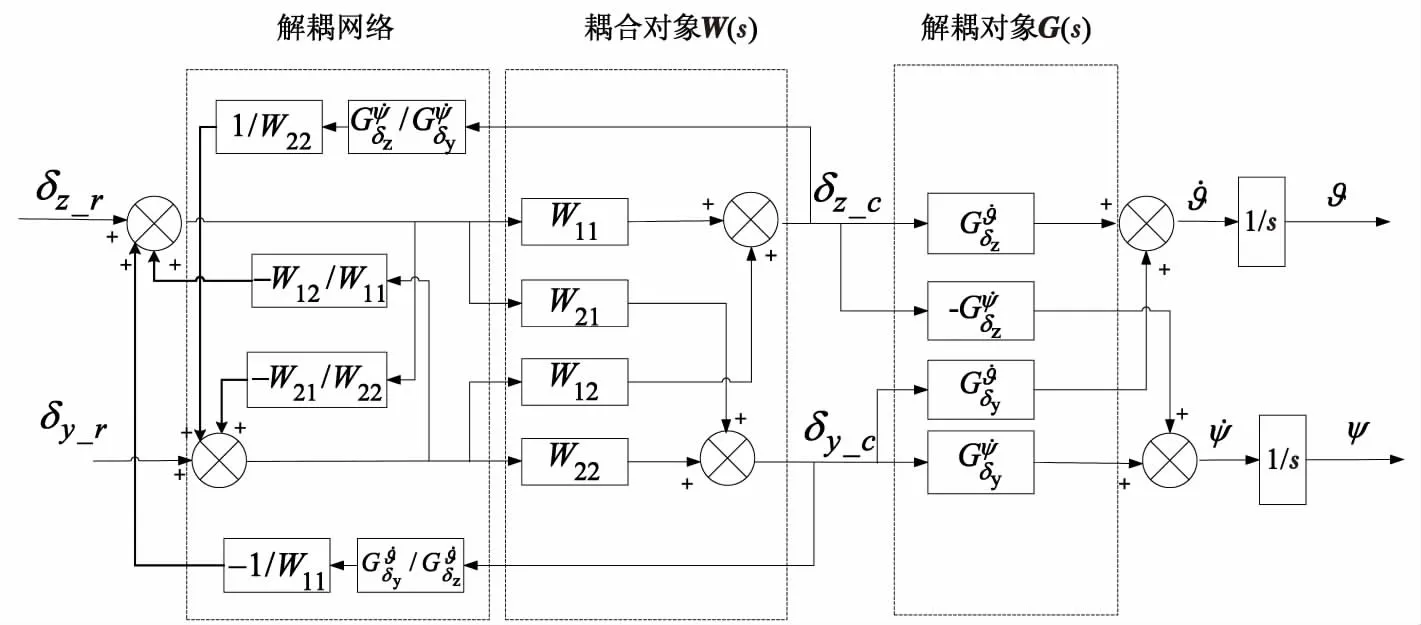
图2 姿态控制系统解耦结构图Fig.2 Decoupling structure diagram of attitude control system

2.4 火箭靶弹过载解耦

2.4.1 过载回路传递函数

由文献[7]可知，前向通道传递函数矩阵Gd为：

(6)

反馈通道传递函数Hd为：

(7)

闭环传递函数Ωd为：

(8)

式中，CS表示由于靶弹姿态运动而引起的加速度，ka表示反馈回路增益，kg表示阻尼回路增益。

2.4.2 过载回路解耦矩阵

由式(1)，式(8)得到过载回路前置反馈补偿解耦矩阵DFG′为：

(9)

旋转靶弹过载回路前置反馈补偿解耦的基本结构如图3所示。

图3 过载回路前置反馈补偿解耦结构图Fig.3 Pre-feedback compensation decoupling structure diagram of overload circuit

由于反馈补偿解耦矩阵DFG′含有速率陀螺和加速度计的反馈信息，因此，欲实现系统的完全解耦，需要得到ka，kg，C。

2.4.3 过载解耦控制系统参数设计

1)加速度计相对质心位置C。本文假设加速度计于质心位置重合，故取值为0。

2)反馈回路增益ka。考虑到靶弹的角运动微分量反馈和阻尼回路增益kg对自动驾驶仪增益的贡献，初步将反馈回路增益ka定为0.8。

3)阻尼回路增益kg。以俯仰通道为例，过载自动驾驶仪的基本结构如图4所示。

图4 过载自动驾驶仪的基本结构Fig.4 Basic structure of overloaded autopilot

得到模型的高阶传递函数简化为：

(10)

用比例增益kS代替舵机环节W(s)，得到过载指令nyc到实际过载ny的闭环传递函数为：

(11)

式(11)中，

其中，V表示靶弹的速度，g表示靶弹的重力加速度，ξN表示自动驾驶仪控制回路在阻尼系数，TN，KN表示系统增益，a22，a24，…，a35称为动力系数，它表征靶弹的运动学特征，其具体物理学意义可由文献[7]给出。

由文献[10]得知：在ξN=0.5，KN=10时，系统在调节时间、响应速度以及超调量等方面较优。将特征点1的动力系数以及其他相关参数代入，可得，ks=0.11，kg=13.3。

3 仿真验证

3.1 姿态解耦控制性能仿真验证

1)解耦前姿态控制系统的俯仰和偏航通道阶跃输入的耦合响应分别如图5和图6所示。

从图5和图6的仿真曲线可以看出系统在未解耦前，偏航和俯仰通道存在明显的耦合响应。正向的俯仰引起正向的偏航以及正向的偏航引起负向的俯仰，而俯仰和偏航引起的交连部分的影响是使其自身不断减小，故滚转靶弹在无控飞行状态下，弹体姿态角运动是呈滚转稳定的。由于阶跃输入中的δz_r、δy_r表示周期平均控制力的最大输入，因此即使靶弹是旋转稳定的，在俯仰和偏航通道的输出响应仍会有震荡并呈向上增加的趋势。

2)解耦后姿态控制系统的俯仰和偏航通道阶跃输入的耦合响应分别如图7和图8所示。

图5 解耦前俯仰通道阶跃输入耦合响应Fig.5 Coupling response of pitch channel step input before decoupling

图6 解耦前偏航通道阶跃输入耦合响应Fig.6 Coupling response of yaw channel step input before decoupling

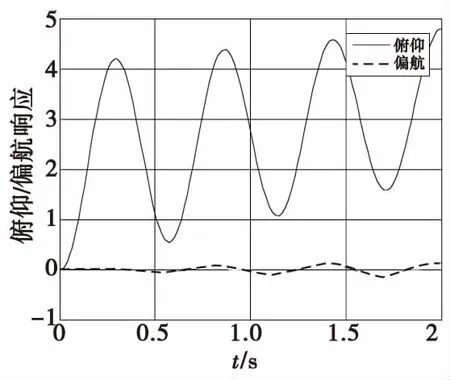
图7 解耦后俯仰通道阶跃输入响应Fig.7 Response of decoupled pitch channel step input

通过图7，图8可以得出，采用前置反馈补偿解耦的方法有效的改善了系统的俯仰-偏航响应，并实现了系统的近似解耦。

3.2 过载解耦控制性能仿真验证

以俯仰通道为例，前置反馈补偿解耦前后，俯仰阶跃输入的俯仰、偏航通道响应分别如图9和图10所示。

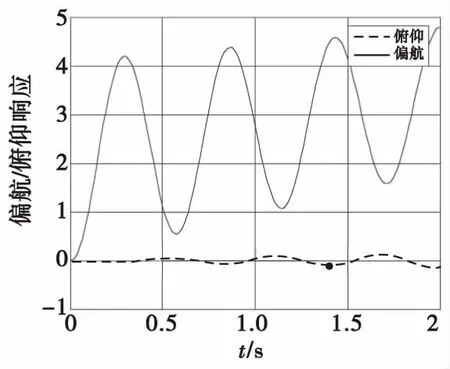
图8 解耦后偏航通道阶跃输入响应Fig.8 Response of decoupled yaw channel step input

图9 解耦前俯仰阶跃输入响应Fig.9 Response of pitch channel step input before decoupling

图10 解耦后俯仰阶跃输入响应Fig.10 Response of decoupled pitch step input

从图9中我们可以得出系统在解耦前，俯仰和偏航通道均受到耦合的作用。其中，耦合使得俯仰通道在稳态值增加了近4%，而俯仰通道的阶跃输入导致偏航通道产生负的交叉响应，使偏航通道引起的最大交叉响应为-0.4，稳态响应为-0.18。在前置反馈补偿解耦后，有效的消除了耦合对俯仰通道的影响，并且使偏航通道引起的最大交叉响应为-0.17左右，稳态响应为0，解耦效果良好。

4 结论

本文提出了基于前置反馈补偿的火箭靶弹解耦方法。该方法在靶弹运动学和控制频域模型基础上，将开环传递函数矩阵分解为运动学耦合和控制耦合，通过引入一个预补偿器，使得运动/控制耦合的传递函数矩阵是对角占优的，便可以将补偿后的俯仰、偏航通道进行单独设计，进而实现靶弹姿态和过载解耦控制系统的设计。仿真结果表明，采用前置反馈补偿解耦方法有效地解决了旋转靶弹俯仰和偏航通道之间的耦合效应，并且具有解耦器结构简单，动态响应性能好等优点，在工程上具有一定的指导意义。